Точкой перегиба кривой называется такая точка, которая отделяет выпуклую часть кривой от вогнутой

Правилонахождения точки перегиба:

1. Находят вторую производную исследуемой функции .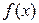

2. Находят все критические точки второго рода из области определения функции (точки, в которых производная второго порядка равна нулю).

3. Устанавливают знаки второй производной функции при переходе через критические точки второго рода. Изменение знака 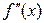указывает на наличие точки перегиба.

4. Находят ординаты точек перегиба.

Задание 37.Исследовать на выпуклость, вогнутость и точки перегиба кривую .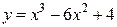

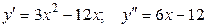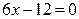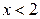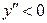Решение: . Из уравнения находим х = 2. Если , то , следовательно, в интервале (-¥; 2) кривая выпукла. Если 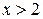, то 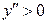, значит, в интервале (2; ¥) кривая вогнута. Итак, при переходе через х = 2 вторая производная 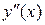меняет знак (с минуса на плюс). Следовательно, кривая имеет точку перегиба, абсцисса которой равна 2.

Подставляя в уравнение кривой х = 2, найдем ординату точки перегиба: 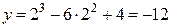. Итак, (2; -12) – точка перегиба.