Возрастающая функция. убывающая функция
Четная функция. Нечетная функция.
§2 Периодичность функций
Понятие периодичности
Как правило, изучение этого свойства функции рекомендуется осуществлять при рассмотрении тригонометрических функций. Подвести учащихся к свойству периодичности функций можно, используя метод целесообразных задач.
1. Используя единичную окружность, докажите тождества (α Î R):
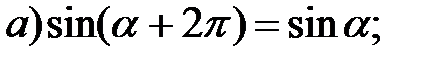
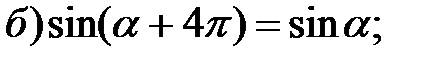
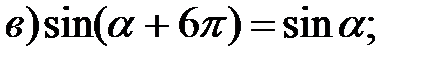
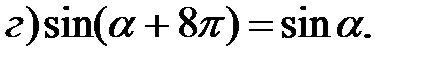
2. Сравните:
а) 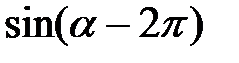 и
и 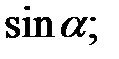
б) 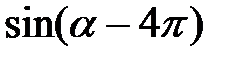 и
и 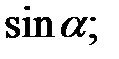
в) 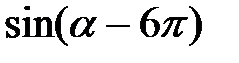 и
и 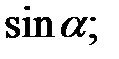
3. Существует ли такое число α, при котором выполняется равенство
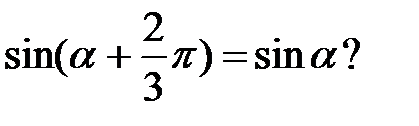
Учащиеся подводятся к выводу: числа вида 2πk (k Î Z) – особые для функции синус. Им сообщается, что эти числа называются периодами функции, а сама функция периодической.
Затем вводится определение: «Функция у = f(x) называется периодической, если существует такое число Т ¹ 0, что при любом х из области определения функции числа х – Т и х + Т также принадлежат этой области и выполняется равенство f(х – Т) = f(x) = f(х + Т)». В этом случае число Т называется периодом функции.
Пример. Функция f(x) = 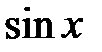 является периодической.
является периодической.
D(f) = R. При любом x Î R (числа (x + 2π) Î R и (x - 2π) Î R) cумма и разность двух действительных чисел – действительные числа. Числам x,
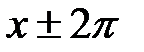 соответствует одна и та же точка единичной окружности, а значит, и одна и та же ордината – значение синуса, поэтому
соответствует одна и та же точка единичной окружности, а значит, и одна и та же ордината – значение синуса, поэтому 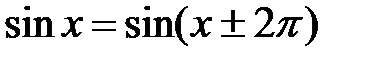
Легко доказать, что функция 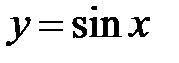 имеет бесконечное множество периодов вида 2πk, где k Î Z : числа 4π, 6π, 8π, ... , -4π, -6π, -8π,... – периоды функции.
имеет бесконечное множество периодов вида 2πk, где k Î Z : числа 4π, 6π, 8π, ... , -4π, -6π, -8π,... – периоды функции.
Число 2π является наименьшим положительным периодом функции синус.
Итак, если Т – период функции, то kT, где k Î Z, - также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. на практике обычно рассматривают наименьший положительный период. Его иногда обозначают Т0.
Свойства периодических функций.
1. Область определения периодической функции симметрична относительно начала координат.
2. Для периодической функции 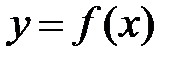 справедливо равенство
справедливо равенство 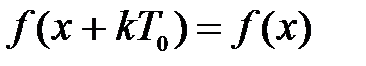 , где Т0 – период функции, к Î Z.
, где Т0 – период функции, к Î Z.
3. Если Т0 – период функции 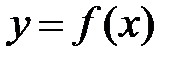 , то любое из чисел kT0, где
, то любое из чисел kT0, где 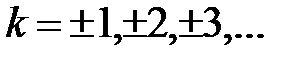 также период этой функции.
также период этой функции.
4. Если функция 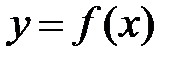 периодическая с периодом Т0, то функция
периодическая с периодом Т0, то функция 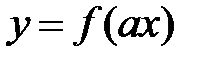 также периодическая с периодом
также периодическая с периодом 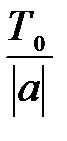 (при а ¹ 0).
(при а ¹ 0).
5. Если функция 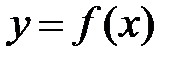 периодическая с периодом Т0, то функции вида
периодическая с периодом Т0, то функции вида 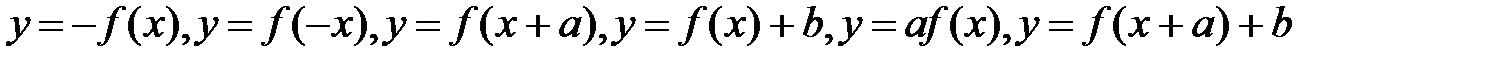 являются периодическими с тем же периодом.
являются периодическими с тем же периодом.
6. Сумма, разность, произведение и частное периодических функций с одинаковым периодом являются периодическими функциями с тем же периодом.
7. Сумма периодических функций с разными периодами является периодической функцией только тогда, когда их периоды соизмеримы.
8. Если 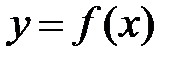 имеет период Т и дифференцируема, то
имеет период Т и дифференцируема, то 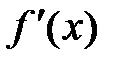 - периодическая функция с тем же периодом.
- периодическая функция с тем же периодом.
