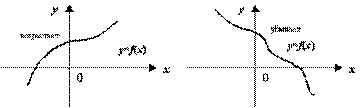
Возрастающая, убывающая функция

Напомним, что функция 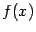называется возрастающей на интервале 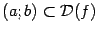, если для любых двух точек 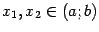из неравенства 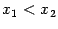следует, что 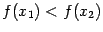; убывающей на интервале 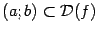, если из неравенства 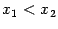следует, что ;

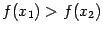Экстремум функции

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Достаточные условия экстремума

Пусть задана z =z (x,y), (x,y) 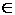D, которая имеет частные производные второго порядка в некоторой окрестности точки M₀(x₀,y₀) 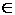D. Причем M₀ - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:

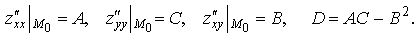
Если:

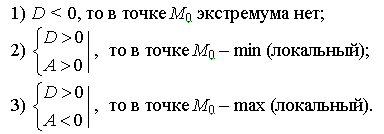
Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.

Необходимые условия экстремума

Пусть задана функция z =z (x,y), (x,y) 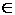D. Точка M₀(x₀;y₀ 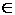D - точка локального экстремума.

Если в этой точке существуют z'_x и z'_y, то

Геометрическое доказательство "очевидно". Если в точке C₀ на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.

Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):

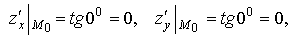
что и требовалось доказать.

50.=33.

Выпуклость и вогнутость

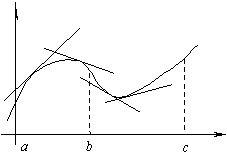
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

52=46

Необходимое условие точки перегиба

Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x₀, f(x₀)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x₀) = 0.

Достаточное условие точки перегиба

Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x₀ интервала (a, b), за исключением, быть может самой точки х₀, а график функции имеет касательную в точке С = (х₀, f (x₀)). Если при переходе через точку х₀ вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).

53.=46

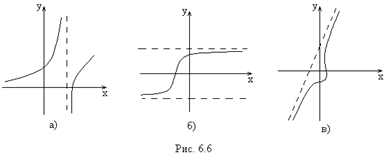
Вертикальная асимптота — прямая вида 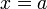при условии существования предела .

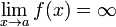Горизонтальная асимптота — прямая вида 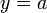при условии существования предела

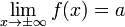
Наклонная асимптота — прямая вида 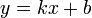при условии существования пределов

1.

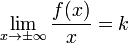
2.

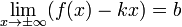
Исследование схема