Ток и плотность тока проводимости
Если в проводнике существует электрическое поле, оно вызывает упорядоченное движение зарядов, представляющих собой ток проводимости.
Свойство среды, характеризующее ее способность проводить ток, называют удельной проводимостью g. Единицей измерения удельной проводимости является сименс на метр (См/м).
Основной величиной в электрическом поле проводящей среды является плотность тока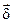 
. Это векторная величина, совпадающая с направлением напряженности электрического поля. Численно плотность тока равна пределу отношения тока Di сквозь элемент поверхности Ds, нормальный к направлению движения заряженных частиц, к этому элементу, когда последний стремится к нулю
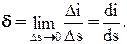
Ток, проходящий сквозь поверхность s конечных размеров, равен
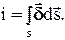
Таким образом, ток есть поток вектора плотности тока.
Характерным отличием тока проводимости от других видов тока является то, что плотность тока проводимости при постоянной температуре пропорциональна напряженности электрического поля. Коэффициентом пропорциональности и является удельная проводимость g
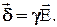(2.1)
Эта формула представляет закон Ома в дифференциальной форме.
Если от обеих частей последнего уравнения взять интеграл по замкнутому контуру, включающему в себя источник электродвижущей силы (ЭДС), то получим второй закон Кирхгофа
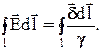
В общем случае говорят, что в замкнутом контуре действует электродвижущая сила е, если линейный интеграл напряженности электрического поля вдоль замкнутого контура не равен нулю, причем этот линейный интеграл равен ЭДС, действующей в контуре:
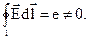
Если рассматривать поле только в области пространства вне источников ЭДС, то будет справедливо уравнение (1.3) и (1.4). Последнее позволяет сделать вывод о том, что вне источников ЭДС электрическое поле постоянных токов является, так же как и электростатическое поле, безвихревым. Такое поле является потенциальным, поэтому для его характеристики может быть введена функция координат U(x,y,z), называемая электрическим потенциалом, причем и в данном случае будет справедливо уравнение (1.7).
2.2. Электрическое поле в диэлектрике, окружающем проводники
с постоянными токами
Поле в диэлектрике характеризуется уравнениями:
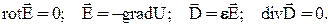
Для однородной среды, когда e = const, эти уравнения дают
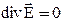или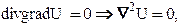 
то есть потенциал удовлетворяет уравнению Лапласа.
Таким образом, в самом диэлектрике такое поле ничем не отличается от электростатического поля. Более того, на поверхности проводящих сред можно пренебрегать касательной составляющей напряженности поля по сравнению с нормальной составляющей, поскольку последняя много больше касательной составляющей и считать поверхности проводников также эквипотенциальными поверхностями без опасения внести в расчет заметную ошибку. В таком случае граничные условия на поверхности проводников оказываются тождественными условиям в электростатике. Поэтому при рассмотрении электрического поля в диэлектрике, окружающем проводники с постоянными токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.