Как исследовать функцию на непрерывность?

Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:

Пример 1

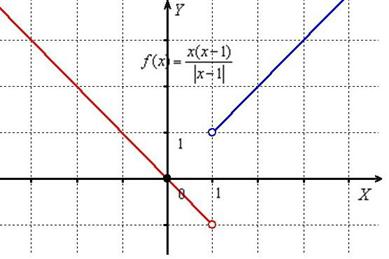
Исследовать функцию 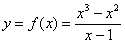на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение:

1) Под прицел попадает единственная точка 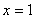, в которой функция не определена.

2) Вычислим односторонние пределы:

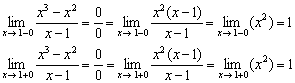
Односторонние пределы конечны и равны.

Таким образом, в точке 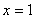функция терпит устранимый разрыв.

Как выглядит график данной функции?

Хочется провести упрощение 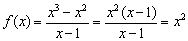, и вроде бы получается обычная парабола. НО исходная функция не определена в точке 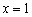, поэтому обязательна следующая оговорка:

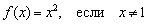
Выполним чертёж:

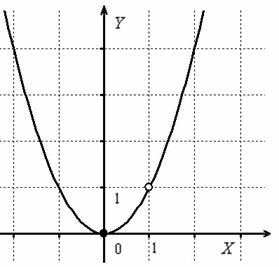
Ответ: функция непрерывна на всей числовой прямой кроме точки 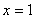, в которой она терпит устранимый разрыв.

Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.

Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.

Разделаемся с любимыми модулями:

Пример 2

Исследовать функцию 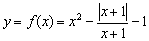на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение: почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков. Поскольку модуль неотрицателен, то он раскрывается следующим образом: 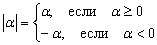, где «альфа» – некоторое выражение. В данном случае 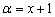, и наша функция должна расписаться кусочным образом:

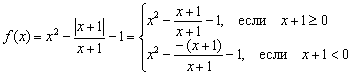
Но дроби обоих кусков предстоит сократить на 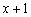. Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке 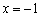, так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие 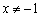, и первое неравенство 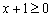сделать строгим:

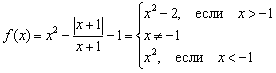
Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения: перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.

Выполним чертёж. В соответствии с нашими выкладками, слева от точки 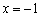необходимо начертить фрагмент параболы 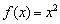(синий цвет), а справа – кусок параболы 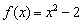(красный цвет), при этом функция не определена в самой точке :

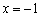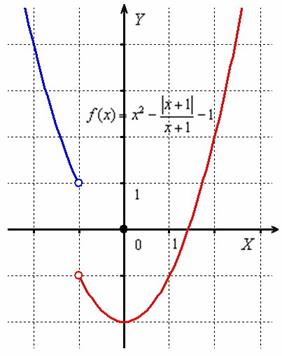
Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию 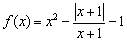(не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.

Исследуем функцию на непрерывность аналитически:

1) Функция не определена в точке 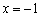, поэтому сразу можно сказать, что не является в ней непрерывной.

2) Установим характер разрыва, для этого вычислим односторонние пределы:

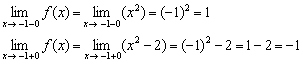
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке 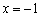. Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.

Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования ;-)) и завершить задание:

Ответ: функция непрерывна на всей числовой прямой кроме точки 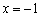, в которой она терпит разрыв первого рода со скачком.

Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: 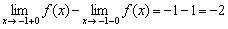, то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).

Пример 3

Исследовать функцию 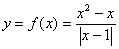на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.

Это пример для самостоятельного решения, примерный образец решения в конце урока.

Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:

Пример 4

Исследовать функцию на непрерывность и построить график функции .

Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства 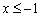значение 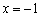принадлежит прямой 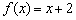(зелёная точка), и в силу неравенство 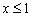значение 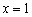принадлежит параболе 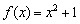(красная точка):

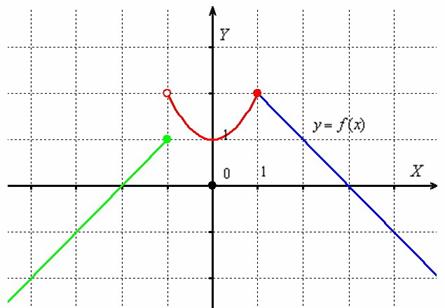
Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:

I) Исследуем на непрерывность точку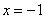

1) 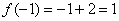– функция определена в данной точке.

2) Найдём односторонние пределы:

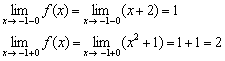
Односторонние пределы конечны и различны, значит, функция 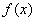терпит разрыв 1-го рода со скачком в точке .

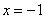Вычислим скачок разрыва как разность правого и левого пределов:
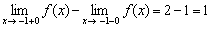, то есть, график рванул на одну единицу вверх.

II) Исследуем на непрерывность точку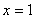

1) 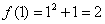– функция определена в данной точке.

2) Найдём односторонние пределы:

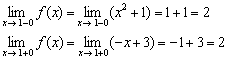
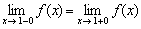– односторонние пределы конечны и равны, значит, существует общий предел.

3) 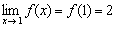– предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция 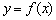непрерывна в точке 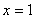по определению непрерывности функции в точке.

На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:

Ответ: функция непрерывна на всей числовой прямой, кроме точки 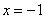, в которой она терпит разрыв первого рода со скачком.

Готово.

Пример 5

Исследовать функцию на непрерывность и построить её график .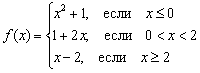

Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.

Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:

Пример 6

Дана функция 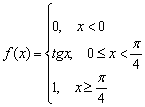. Исследовать функцию на непрерывность в точках 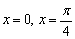. Построить график.

Решение: и снова сразу выполним чертёж на черновике:

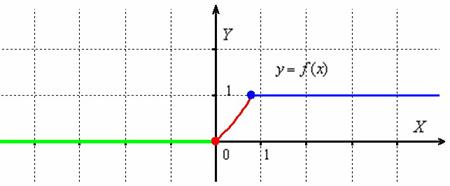
Особенность данного графика состоит в том, что при 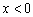кусочная функция задаётся уравнением оси абсцисс 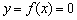. Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение 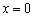относится к ветке тангенса (красная точка), а значение 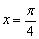принадлежит прямой .

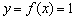Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4 подобных примеров:

I) Исследуем на непрерывность точку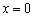

1) 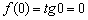– функция определена в данной точке.

2) Вычислим односторонние пределы:

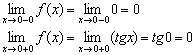
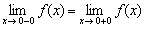, значит, общий предел существует.

На всякий пожарный напомню тривиальный факт: предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).

Едем дальше:

3) 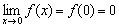– предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция 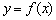непрерывна в точке 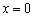по определению непрерывности функции в точке.

II) Исследуем на непрерывность точку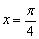

1) 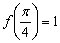– функция определена в данной точке.

2) Найдём односторонние пределы:

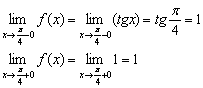
И здесь – предел единицы равен самой единице.

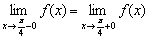– общий предел существует.

3) 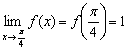– предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция 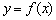непрерывна в точке 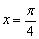по определению непрерывности функции в точке.

Как обычно, после исследования переносим наш чертёж на чистовик.

Ответ: функция непрерывна в точках .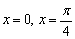

Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).

Небольшая математическая «скороговорка» для самостоятельного решения:

Пример 7

Дана функция 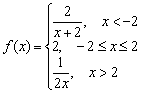. Исследовать функцию на непрерывность в точках 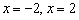. Классифицировать точки разрыва, если они есть. Выполнить чертёж.

Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет ;-)

Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:

Пример 8

Исследовать на непрерывность функцию 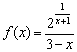и построить её схематический график.

Решение: нехорошие точки очевидны: 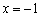(обращает в ноль знаменатель показателя) и 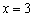(обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование:

I)Исследуем на непрерывность точку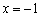

1) Функция не определена в данной точке.

2) Найдём односторонние пределы:

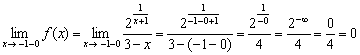
Обратите внимание на типовой приём вычисления одностороннего предела: в функцию вместо «икса» мы подставляем 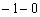. В знаменателе никакого криминала: «добавка» «минус ноль» не играет роли, и получается «четыре». А вот в числителе происходит небольшой триллер: сначала в знаменателе показателя 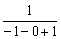убиваем –1 и 1, в результате чего получается 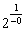. Единица, делённая на бесконечно малое отрицательное число, равна «минус бесконечности», следовательно: 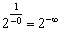. И, наконец, «двойка» в бесконечно большой отрицательной степени равна нулю: 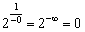. Или, если ещё подробнее: .

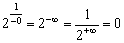Вычислим правосторонний предел:

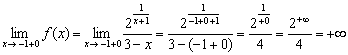
И здесь – вместо «икса» подставляем . В знаменателе «добавка» снова не играет роли: 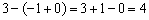. В числителе проводятся аналогичные предыдущему пределу действия: уничтожаем противоположные числа и делим единицу набесконечно малое положительное число: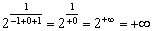

Правосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .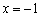

II)Исследуем на непрерывность точку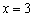

1) Функция не определена в данной точке.

2) Вычислим левосторонний предел:

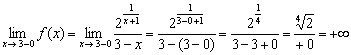
Метод такой же: подставляем в функцию вместо «икса» 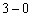. В числителе ничего интересного – получается конечное положительно число 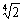. А в знаменателе раскрываем скобки, убираем «тройки», и решающую роль играет «добавка» .

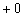По итогу, конечное положительное число, делённое на бесконечно малое положительное число, даёт «плюс бесконечность»: .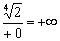

Правосторонний предел, как брат близнец, за тем лишь исключением, что в знаменателе выплывает бесконечно малое отрицательное число:

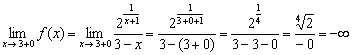
Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке .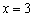

Таким образом, у нас две точки разрыва, и, очевидно, три ветки графика. Для каждой ветки целесообразно провести поточечное построение, т.е. взять несколько значений «икс» и подставить их в 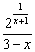. Заметьте, что по условию допускается построениесхематического чертежа, и такое послабление естественно для ручной работы. Я строю графики с помощью проги, поэтому не имею подобных затруднений, вот достаточно точная картинка:

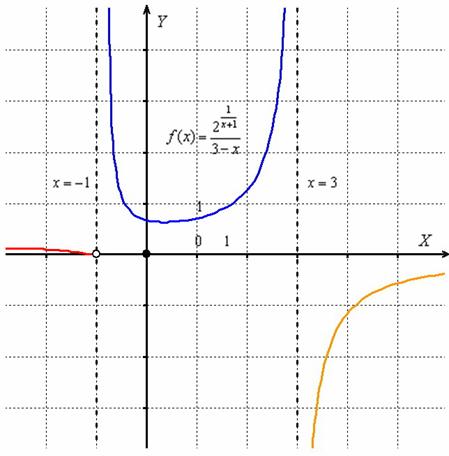
Прямые 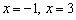являются вертикальными асимптотами для графика данной функции.

Ответ: функция непрерывна на всей числовой прямой кроме точек 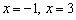, в которых она терпит разрывы 2-го рода.

Более простая функция для самостоятельного решения:

Пример 9

Исследовать на непрерывность функцию 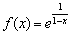и выполнить схематический чертёж.

Примерный образец решения в конце, который подкрался незаметно.

До скорых встреч!

Решения и ответы:

Пример 3: Решение: преобразуем функцию: 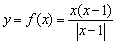. Учитывая правило раскрытия модуля 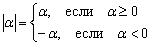и тот факт, что 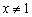, перепишем функцию в кусочном виде:

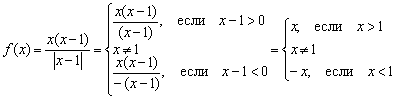
Исследуем функцию на непрерывность.
1) Функция не определена в точке .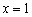
2) Вычислим односторонние пределы:

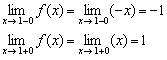
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке 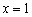. Выполним чертёж: