Дифференциалы высших порядков. Пусть , тогда – дифференциал первого порядка

Пусть 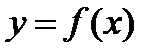, тогда 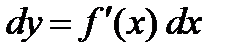– дифференциал первого порядка. Дифференциал второго порядка 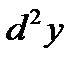– дифференциал от дифференциала первого порядка, при этом, если 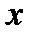независимая переменная, то при вторичном дифференцировании 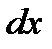считается независимым от 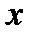и выносится как .

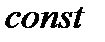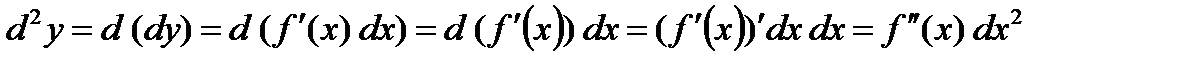, (2)

здесь .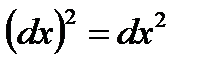

,

…

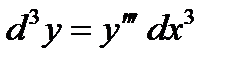Полученные выражения дают возможность записать производные как

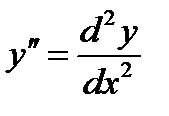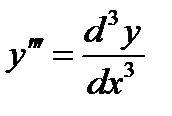, (3)

и так далее.

Если 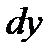имел первый порядок малости в сравнении с 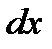, то 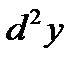имеет второй порядок малости, 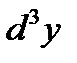– третий и так далее. Отметим, что

,

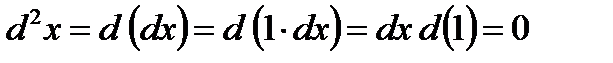то есть второй дифференциал независимой переменной равен нулю.

Замечание. Если 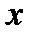не является независимой переменной (или нам неизвестно), формула (1) все равно справедлива. Однако при ее дальнейшем дифференцировании 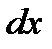уже нельзя считать 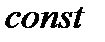, надо использовать правило дифференцирования произведения

.

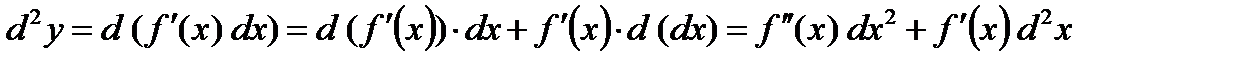Если теперь окажется, что 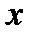– независимая переменная, то

.

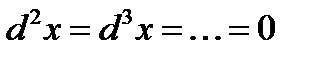Итак, формулы (1)-(3) могут использоваться, если 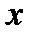– независимая переменная.