Пример 1. Найти производную в точку x0
Найти производную в точку x0.
1) 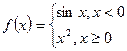
Найдем односторонние пределы:
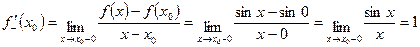
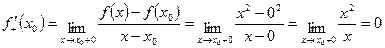
Так как 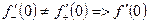 - не существует.
- не существует.
2)Найти производную в точке x0.
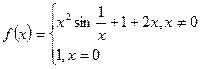
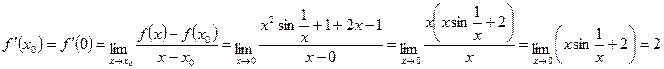 Соответственно,
Соответственно, 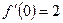
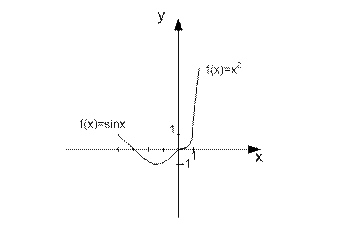
Геометрический смысл производной
Дан график функции y=f(x).
Проведем секущую через точки A(x0,y0) и B(x0+Δx, y0+Δy)
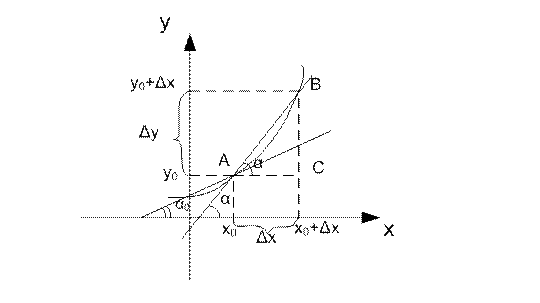
Если обозначить разность ординат этих точек через Δy, то 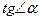 , образованного секущей с осью Ox, можно представить следующим образом:
, образованного секущей с осью Ox, можно представить следующим образом:
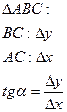
Если 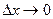 , то точка B будет стремиться по функции точки А, тогда секущая при совпадении точек А и B превращается в касательную графика функции f(x) в точке А. Обозначим через α0 угол, образованный касательной и положительным направлением оси x:
, то точка B будет стремиться по функции точки А, тогда секущая при совпадении точек А и B превращается в касательную графика функции f(x) в точке А. Обозначим через α0 угол, образованный касательной и положительным направлением оси x:
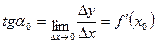
Вывод: Следовательно, значение производной функции 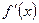 в любой точке x равно
в любой точке x равно 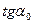 , касательной к графику f(x) в точке x0 (
, касательной к графику f(x) в точке x0 ( 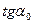 -угловой коэффициент).
-угловой коэффициент).
