Признак коши сходимости числового ряда.

Радикальный признак Коши применяется, когда выражение общего члена находится в степени, зависящей от n. Например, .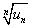

Пусть существует предел

.

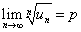Тогда

если 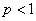, то ряд сходится,

а если 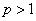, то ряд расходится.

Если же 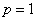, то ничего определённого о сходимости ряда сказать нельзя: радикальный признак Коши здесь не годится и нужно использовать другой признак.

Пример 1.Исследовать сходимость ряда

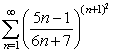
Решение. Применяем радикальный признак Коши - находим предел:

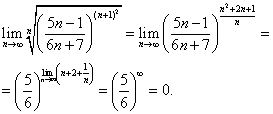
Так как 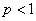, ряд сходится.

Пример 2.Исследовать сходимость ряда

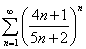
Решение. Применяем радикальный признак Коши - находим предел:

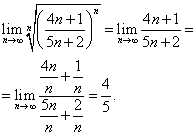
Так как 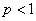, ряд сходится.

Интегральный признак Коши

Пусть дан ряд 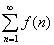, члены которого являются значениями некоторой функции f(x), положительной, непрерывной и убывающей на полуинтервале 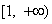. Тогда,

если интеграл 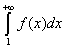сходится, то сходится и ряд ;

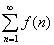если же интеграл 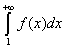расходится, то и ряд 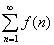также расходится.

Пример 3.Исследовать сходимость ряда

.

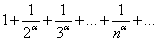Решение. Так как интеграл 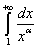сходится при 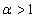и расходится при 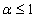, то, согласно интегральному признаку Коши, и данный ряд сходится при 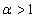и расходится при .

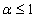Ряды с произвольными членами.

Числовой ряд 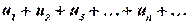(22)

называется рядом с произвольными членами, если в нем имеется бесконечное множество положительных членов и бесконечное множество отрицательных членов.

Частным видом ряда с произвольными членами является ряд со знакочередующимися членами.

Определение 7. Числовой ряд (22) называется абсолютно сходящимся, если сходится ряд, составленный из модулей членов этого ряда: 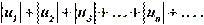(23)

Пусть ряд (22) сходится абсолютно, это значит, по определению, что сходится ряд (23). Возникает вопрос, а сходится ли сам ряд (22)? Ответ дает теорема.

Теорема 15.Абсолютно сходящийся ряд есть ряд сходящийся.

Определение 8. Числовой ряд (22) называется не абсолютно сходящимся, если он сходится, а ряд, составленный из модулей его членов, т.е. ряд (23) расходится. Не абсолютно сходящийся ряд называется условно сходящимся.

Пример 16.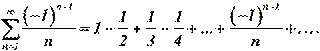

Решение. Этот ряд со знакочередующимися членами, его члены убывают по модулю, и 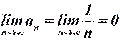. Ряд сходится по теореме Лейбница. Запишем ряд, состоящий из модулей: 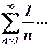гармонический ряд. Он расходится. Следовательно, исходный ряд сходится условно.

Пример 17.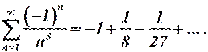

Решение. Этот ряд со знакочередующимися членами. Он сходится по теореме Лейбница. Запишем ряд, состоящий из модулей: 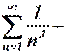обобщенный гармонический ряд. Он сходится при 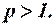Значит, исходный ряд сходится абсолютно.

Знакочередующиеся ряды.

Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.

Или в два пункта:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю: 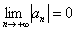. Причём, убывают монотонно.

Если выполненыобаусловия, то ряд сходится.

Краткая справка о модуле приведена в методичкеГорячие формулы школьного курса математики, но для удобства ещё раз:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду 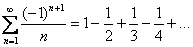. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:

– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю: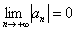

17.Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимость

Для того чтобы понять примеры данного урока необходимо хорошо ориентироваться в положительных числовых рядах: понимать, что такое ряд, знать необходимый признак сходимости ряда, уметь применять признаки сравнения, признак Даламбера, признаки Коши. Тему можно поднять практически с нуля, последовательно изучив статьи Ряды для чайников и Признак Даламбера. Признаки Коши. Логически этот урок является третьим по счёту, и он позволит не только разобраться в знакочередующихся рядах, но и закрепить уже пройденный материал! Какой-то новизны будет немного, и освоить знакочередующиеся ряды не составит большого труда. Всё просто и доступно.

Что такое знакочередующийся ряд?Это понятно или почти понятно уже из самого названия. Сразу простейший пример.

Рассмотрим ряд 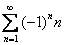и распишем его подробнее:

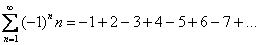
А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.

Знакочередование обеспечивает множитель 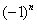: если 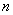чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».

В практических примерах знакочередование членов ряда может обеспечивать не только множитель 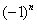, но и его родные братья: 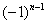, , 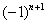, 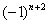…. Например:

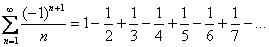
Подводным камнем являются «обманки»: 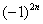, , 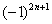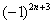и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном 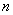: 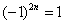, , 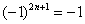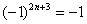. Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.

Как исследовать знакочередующийся ряд на сходимость?Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга.

Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.

Или в два пункта:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю: 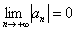. Причём, убывают монотонно.

Если выполнены оба условия, то ряд сходится.

Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду 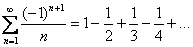. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:

– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю: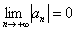

Конец справки

Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство.

Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: 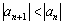. Для ряда 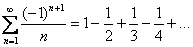выполнена строгая монотонность убывания, её можно расписать подробно:

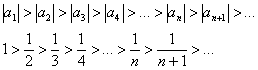
А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: .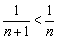

Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: 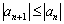. Рассмотрим ряд с факториалом: 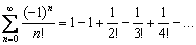Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: .

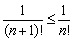В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). Кроме того, члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.

Не нужно пугаться того, что я нагородил, практические примеры всё расставят по своим местам:

Пример 1

Исследовать ряд на сходимость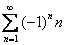

В общий член ряда входит множитель 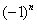, а значит, нужно использовать признак Лейбница

1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно 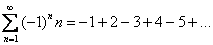и выносят вердикт «Ряд является знакочередующимся».

2) Убывают ли члены ряда по модулю? Необходимо решить предел 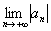, который чаще всего является очень простым.

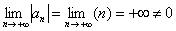– члены ряда не убывают по модулю. К слову, отпала надобность в рассуждениях о монотонности убывания.

Вывод: ряд расходится.

Как разобраться, чему равно 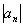? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить 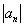, нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда 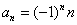. Тупо убираем «мигалку»: .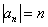