Метод вариации произвольной постоянной

Уравнения, приводящиеся к ДУ в полных дифференциалах

Иногда ур-е 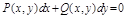не явл. Ур-ем в полных дифференциалах 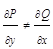. Удаётся подобрать некоторую ф-цию 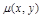: 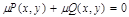становится ур-ем. Ф-ция 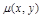назыв. инт множителем, тогда:

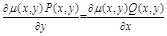. Всякая функция, удовлетворяющая 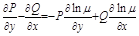является интегрирующим множителем.

I. Случай инт. множителя, зависящего только от х:

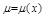, тогда 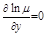, 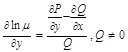при этом 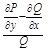должно зависеть только от х иначе 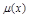не существует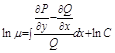

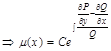
II. Случай инт. множителя, зависящего только от y: 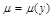, тогда 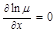, 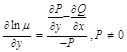при этом

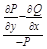должно зависеть только от y иначе 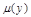не существует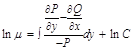

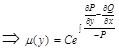
III. Случай инт. множителя, вида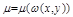

, ,

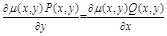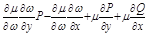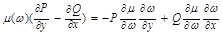
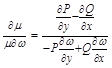
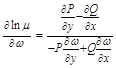
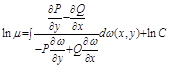
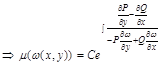
Огибающие семейства кривых. Особые решение

Мн-во точек (х,у) в которых нарушается единственность решений ур-я F(x,y,y’)=0 называется особым мн-вом. Только среди точек кривой Ф(х,у)=0 называемой р-дискриминантной кривой чаще записываются в виде F(x,y,p)=0 и ,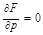

могут быть точками особого мн-ва . Если какая-нибудь ветвь 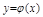кривой Ф(х,у)=0 принадлежит особому множеству и в тоже время явл. Интегральной кривой, то она называется особой интегральной кривой, а функция 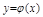называется особым решением. Для нахождения особого решения ур-я F(x,y,y’)=0 надо найти р-дискриминантную кривую, определяемую ур-ем: F(x,y,р)=0,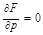

ДУ высших порядков, основные понятия ДУ, допускающих понижения порядка

Общий вид

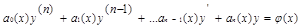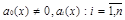(1) , ф-ции определённые в некоторой обл. D, если 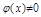, то (1) –линейное неоднородное.

Общее решение ДУ n-ного порядка-мн-во решений, состоящих из всех частных решений без исключений, иначе (1)-линейное однородное.

ДУ, допускающих понижения порядка

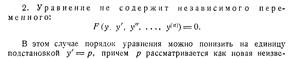
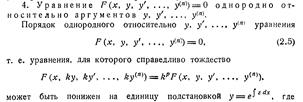
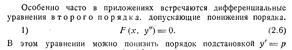
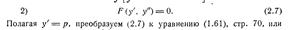
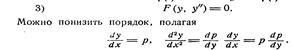
Св-во решений линейных однородных ДУ n-го порядка

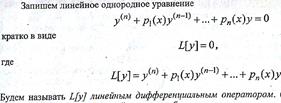
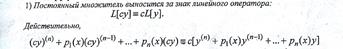
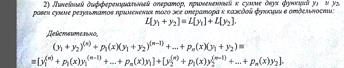
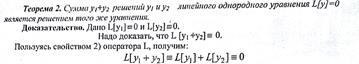
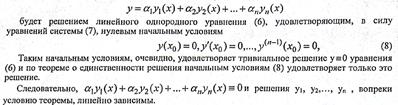
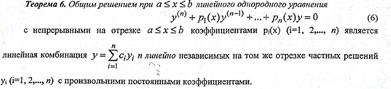
Лин. Одн. ДУ 2 порядка с переменными коефициентами. Ф-ла Остроградского-Лиувилля

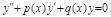(1)

Определитель Вронского имеет вид

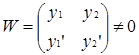если у₁ и у₂ лин-независимы, иначе определитель=0

Th Если известно 1 частное решение (1), то нахождение его общего решения сводится к интегрированию ф-ции

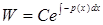-Формула Остроградского-Лиувилля. Линейное уравнение 1-го порядка:

……

…..

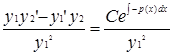
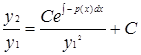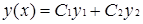
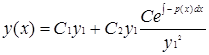
ЛНДУ n-го порядка с постоянными коефициентами. Нахождение частного решения по виду правой части

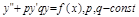
Общее решение:

У_неодн(х)=у_одн(х)+у_част(х)

1) Правая часть первого типа

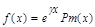, где ɤ-критическое число, Pm(x)-многочлен степени m

y^*(x)= 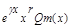, где r-число корней характеристического ур-я совпавших с критическим числом, Qm(x)- многочлен степени m

2) Правая часть второго типа

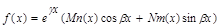
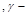критическое число, Mn(x), Nm(x)-многочлены степени n и m

y^*(x)= 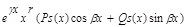, где r-число корней характеристического ур-я совпавших с критическим числом, Ps(x) Qs(x)- многочлен степени s,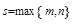

Метод вариации произвольной постоянной

Сущность метода- ищется решение однородного ДУ в виде:

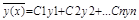
2. Ищется частное решение исходного неодн. Ур-я в виде
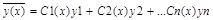, где C_i(x) определяются из системы

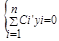
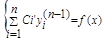
3. Общее решение записывается в виде

Унеодн(х)=уодн(х)+участ(х)