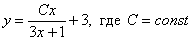Дифференциальные уравнения первого порядка. Примеры решений.Дифференциальные уравнения с разделяющимися переменными

Дифференциальные уравнения (ДУ). Эти два слова обычно приводят в ужас среднестатистического обывателя. Дифференциальные уравнения кажутся чем-то запредельным и трудным в освоении и многим студентам. Уууууу… дифференциальные уравнения, как бы мне всё это пережить?!

Такое мнение и такой настрой в корне неверен, потому-что на самом делеДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ – ЭТО ПРОСТО И ДАЖЕ УВЛЕКАТЕЛЬНО. Что нужно знать и уметь, для того чтобы научиться решать дифференциальные уравнения? Для успешного изучения диффуров вы должны хорошо уметь интегрировать и дифференцировать. Чем качественнее изучены темы Производная функции одной переменной иНеопределенный интеграл, тем будет легче разобраться в дифференциальных уравнениях. Скажу больше, если у вас более или менее приличные навыки интегрирования, то тема практически освоена! Чем больше интегралов различных типов вы умеете решать – тем лучше. Почему? Потому что придется много интегрировать. И дифференцировать. Такженастоятельно рекомендую научиться находить производную от функции, заданной неявно.

В 95% случаев в контрольных работах встречаются 3 типа дифференциальных уравнений первого порядка: уравнения с разделяющимися переменными, которые мы рассмотрим на этом уроке; однородные уравнения и линейные неоднородные уравнения. Начинающим изучать диффуры советую ознакомиться с уроками именно в таком порядке. Есть еще более редкие типы дифференциальных уравнений: уравнения в полных дифференциалах, уравнения Бернулли и некоторые другие. Наиболее важными из двух последних видов являются уравнения в полных дифференциалах, поскольку помимо данного ДУ я рассматриваю новый материал – частное интегрирование.

Сначала вспомним обычные уравнения. Они содержат переменные и числа. Простейший пример: 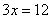. Что значит решить обычное уравнение? Это значит, найди множество чисел, которые удовлетворяют данному уравнению. Легко заметить, что детское уравнение 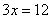имеет единственный корень: 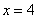. Для прикола сделаем проверку, подставим найденный корень в наше уравнение:

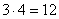
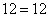– получено верное равенство, значит, решение найдено правильно.

Диффуры устроены примерно так же!

Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную ;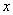
2) зависимую переменную 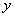(функцию);
3) первую производную функции: .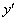

В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная 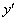, и не было производных высших порядков – 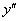, 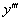и т.д.

Что значит решить дифференциальное уравнение?Решить дифференциальное уравнение – это значит, найти множество функций 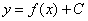, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

Пример 1

Решить дифференциальное уравнение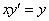

Полный боекомплект. С чего начать решение любого дифференциального уравнения первого порядка?

В первую очередь нужно переписать производную немного в другом виде. Вспоминаем громоздкое обозначение производной: 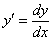. Такое обозначение производной многим из вас наверняка казалось нелепым и ненужным, но в диффурах рулит именно оно!

Итак, на первом этапе переписываем производную в нужном нам виде:

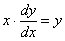
На втором этапе всегда смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.

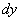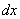Дифференциалы и – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:

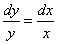
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».

Следующий этап – интегрирование дифференциального уравнения. Всё просто, навешиваем интегралы на обе части:

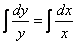
Разумеется, интегралы нужно взять. В данном случае они табличные:

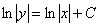
Как мы помним, к любой первообразной приписывается константа. Здесь два интеграла, но константу 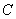достаточно записать один раз. Почти всегда её приписывают в правой части.

Строго говоря, после того, как взяты интегралы, дифференциальное уравнение считается решенным. Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть, 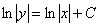– это общий интеграл.

Теперь нужно попробовать найти общее решение, то есть попытаться представить функцию в явном виде.

Пожалуйста, запомните первый технический приём, он очень распространен и часто применяется в практических заданиях. Когда в правой части после интегрирования появляется логарифм, то константу почти всегда целесообразно записать тоже под логарифмом.

То есть, вместозаписи 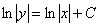обычно пишут .

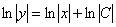Здесь 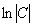– это такая же полноценная константа, как и 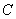. Зачем это нужно? А для того, чтобы легче было выразить «игрек». Используем школьное свойство логарифмов: 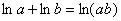. В данном случае:

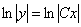
Теперь логарифмы и модули можно с чистой совестью убрать с обеих частей:

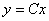
Функция представлена в явном виде. Это и есть общее решение.

Множество функций 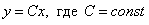является общим решением дифференциального уравнения .

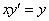Придавая константе 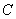различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Любая из функций 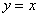, , 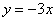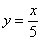и т.д. будет удовлетворять дифференциальному уравнению .

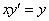Иногда общее решение называют семейством функций. В данном примере общее решение 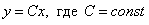– это семейство линейных функций, а точнее, семейство прямых пропорциональностей.

Многие дифференциальные уравнения довольно легко проверить. Делается это очень просто, берём найденное решение 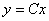и находим производную:

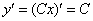
Подставляем наше решение 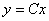и найденную производную 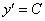в исходное уравнение :

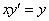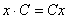
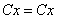– получено верное равенство, значит, решение найдено правильно. Иными словами, общее решение 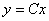удовлетворяет уравнению .

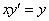После обстоятельного разжевывания первого примера уместно ответить на несколько наивных вопросов о дифференциальных уравнениях.

1) В этом примере нам удалось разделить переменные: 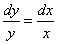. Всегда ли это можно сделать? Нет, не всегда. И даже чаще переменные разделить нельзя. Например, воднородных уравнениях первого порядка, необходимо сначала провести замену. В других типах уравнений, например, в линейном неоднородном уравнении первого порядка, нужно использовать различные приёмы и методы для нахождения общего решения. Уравнения с разделяющимися переменными, которые мы рассматриваем на первом уроке – простейший тип дифференциальных уравнений.

2) Всегда ли можно проинтегрировать дифференциальное уравнение? Нет, не всегда. Очень легко придумать «навороченное» уравнение, которое не проинтегрировать, кроме того, существуют неберущиеся интегралы. Но подобные ДУ можно решить приближенно с помощью специальных методов. Даламбер и Коши гарантируют. …тьфу, lurkmore.ru давеча начитался.

3) В данном примере мы получили решение в виде общего интеграла 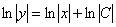. Всегда ли можно из общего интеграла найти общее решение, то есть, выразить «игрек» в явном виде? Нет не всегда. Например: 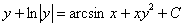. Ну и как тут выразить «игрек»?! В таких случаях ответ следует записать в виде общего интеграла. Кроме того, иногда общее решение найти можно, но оно записывается настолько громоздко и коряво, что уж лучше оставить ответ в виде общего интеграла

Торопиться не будем. Еще одно простое ДУ и еще один типовой приём решения.

Пример 2

Найти частное решение дифференциального уравнения 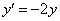, удовлетворяющее начальному условию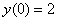

По условию требуется найти частное решение ДУ, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.

Сначала находим общее решение. В уравнении нет переменной «икс», но это не должно смущать, главное, в нём есть первая производная.

Переписываем производную в нужном виде:

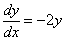
Очевидно, что переменные можно разделить, мальчики – налево, девочки – направо:

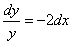
Интегрируем уравнение:

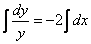
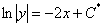
Общий интеграл получен. Здесь константу я нарисовал с надстрочной звездочкой, дело в том, что очень скоро она превратится в другую константу.

Теперь пробуем общий интеграл преобразовать в общее решение (выразить «игрек» в явном виде). Вспоминаем старое, доброе, школьное: 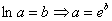. В данном случае:

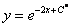
Константа в показателе смотрится как-то некошерно, поэтому её обычно спускают с небес на землю. Если подробно, то происходит это так. Используя свойство степеней, перепишем функцию следующим образом:

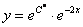
Если 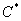– это константа, то 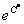– тоже некоторая константа, которую обозначим через букву :

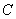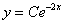
Запомните «снос» константы, это второй технический приём, который часто используют в ходе решения дифференциальных уравнений.

Итак, общее решение: 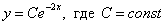. Такое вот симпатичное семейство экспоненциальных функций.

На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию 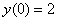. Это тоже просто.

В чём состоит задача? Необходимо подобрать такое значение константы 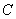, чтобы выполнялось заданное начальное условие .

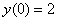Оформить можно по-разному, но понятнее всего, пожалуй, будет так. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:



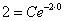
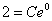
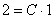
То есть,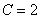

Стандартная версия оформления:

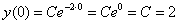
В общее решение 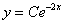подставляем найденное значение константы :
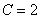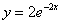– это и есть нужное нам частное решение.

Выполним проверку. Проверка частного решение включает в себя два этапа.

Сначала необходимо проверить, а действительно ли найденное частное решение 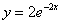удовлетворяет начальному условию 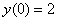? Вместо «икса» подставляем ноль и смотрим, что получится:
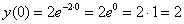– да, действительно получена двойка, значит, начальное условие выполняется.

Второй этап уже знаком. Берём полученное частное решение 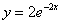и находим производную:

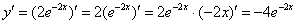
Подставляем 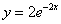и 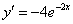в исходное уравнение :

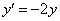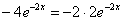
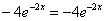– получено верное равенство.

Вывод: частное решение найдено правильно.

Переходим к более содержательным примерам.

Пример 3

Решить дифференциальное уравнение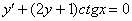

Решение: Переписываем производную в нужном нам виде:

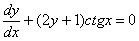
Оцениваем, можно ли разделить переменные? Можно. Переносим второе слагаемое в правую часть со сменой знака:

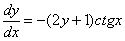
И перекидываем множители по правилу пропорции:

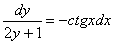
Переменные разделены, интегрируем обе части:

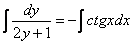
Должен предупредить, приближается судный день. Если вы плохо изучили неопределенные интегралы, прорешали мало примеров, то деваться некуда – придется их осваивать сейчас.

Интеграл левой части легко найти методом подведения функции под знак дифференциала, с интегралом от котангенса расправляемся стандартным приемом, который мы рассматривали на уроке Интегрирование тригонометрических функций в прошлом году:

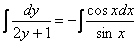
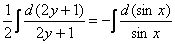
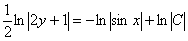
В правой части у нас получился логарифм, согласно моей первой технической рекомендации, в этом случае константу тоже следует записать под логарифмом.

Теперь пробуем упростить общий интеграл. Поскольку у нас одни логарифмы, то от них вполне можно (и нужно) избавиться. Максимально «упаковываем» логарифмы. Упаковка проводится с помощью трёх свойств:

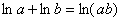
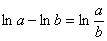
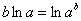
Пожалуйста, перепишите эти три формулы к себе в рабочую тетрадь, при решении диффуров они применяются очень часто.

Решение распишу очень подробно:

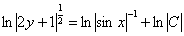
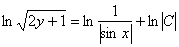
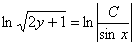
Упаковка завершена, убираем логарифмы:

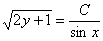
Можно ли выразить «игрек»? Можно. Надо возвести в квадрат обе части. Но делать этого не нужно.

Третий технический совет: Если для получения общего решения нужно возводить в степень или извлекать корни, то в большинстве случаев следует воздержаться от этих действий и оставить ответ в виде общего интеграла. Дело в том, что общее решение будет смотреться вычурно и ужасно – с большими корнями, знаками .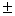

Поэтому ответ запишем в виде общего интеграла. Хорошим тоном считается представить общий интеграл в виде 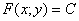, то есть, в правой части, по возможности, оставить только константу. Делать это не обязательно, но всегда же выгодно порадовать профессора ;-)

Ответ: общий интеграл: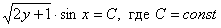

Примечание: общий интеграл любого уравнения можно записать не единственным способом. Таким образом, если у вас не совпал результат с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.

Общий интеграл тоже проверяется довольно легко, главное, уметь находить производные от функции, заданной неявно. Дифференцируем ответ:

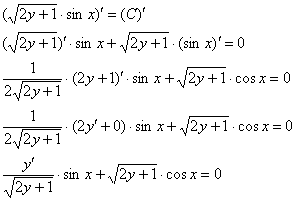
Умножаем оба слагаемых на :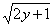

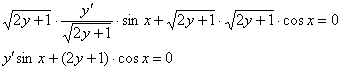
И делим на :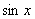

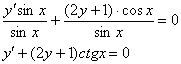
Получено в точности исходное дифференциальное уравнение 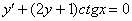, значит, общий интеграл найден правильно.

Пример 4

Найти частное решение дифференциального уравнения 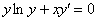, удовлетворяющее начальному условию 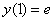. Выполнить проверку.

Это пример для самостоятельного решения. Напоминаю, что задача Коши состоит из двух этапов:
1) Нахождение общего решение.
2) Нахождение частного решения.

Проверка тоже проводится в два этапа (см. также образец Примера 2), нужно:
1) Убедиться, что найденное частное решение действительно удовлетворяет начальному условию.
2) Проверить, что частное решение вообще удовлетворяет дифференциальному уравнению.

Полное решение и ответ в конце урока.

Пример 5

Найти частное решение дифференциального уравнения 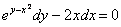, удовлетворяющее начальному условию 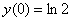. Выполнить проверку.

Решение:Сначала найдем общее решение.Данное уравнение уже содержит готовые дифференциалы 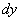и 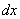, а значит, решение упрощается. Разделяем переменные:

Интегрируем уравнение:

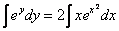
Интеграл слева – табличный, интеграл справа – берем методом подведения функции под знак дифференциала:

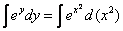
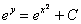
Общий интеграл получен, нельзя ли удачно выразить общее решение? Можно. Навешиваем логарифмы:

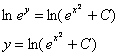
(Надеюсь, всем понятно преобразование 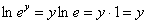, такие вещи надо бы уже знать)

Итак, общее решение:

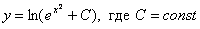
Найдем частное решение, соответствующее заданному начальному условию 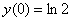. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

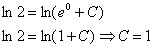
Более привычное оформление: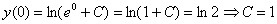

Подставляем найденное значение константы 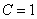в общее решение.

Ответ: частное решение: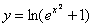

Проверка: Сначала проверим, выполнено ли начальное условие :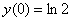
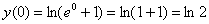– всё гуд.

Теперь проверим, а удовлетворяет ли вообще найденное частное решение 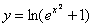дифференциальному уравнению. Находим производную:

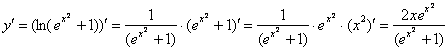
Смотрим на исходное уравнение: 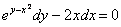– оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал :

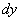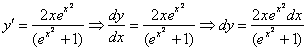
Подставим найденное частное решение 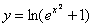и полученный дифференциал в исходное уравнение :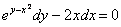

Используем основное логарифмическое тождество :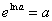

Получено верное равенство, значит, частное решение найдено правильно.

Второй способ проверки зеркален и более привычен: из уравнения 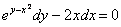выразим производную, для этого разделим все штуки на :

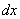И в преобразованное ДУ подставим полученное частное решение 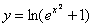и найденную производную . В результате упрощений тоже должно получиться верное равенство.

Пример 6

Решить дифференциальное уравнение 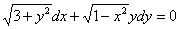. Ответ представить в виде общего интеграла .

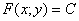Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Какие трудности подстерегают при решении дифференциальных уравнений с разделяющимися переменными?

1) Не всегда очевидно (особенно, чайнику), что переменные можно разделить. Рассмотрим условный пример: 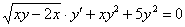. Здесь нужно провести вынесение множителей за скобки: 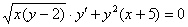и отделить корни: 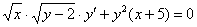. Как действовать дальше – понятно.

2) Сложности при самом интегрировании. Интегралы нередко возникают не самые простые, и если есть изъяны в навыках нахождения неопределенного интеграла, то со многими диффурами придется туго. К тому же у составителей сборников и методичек популярна логика «раз уж дифференциальное уравнение является простым, то пусть интегралы будут посложнее».

3) Преобразования с константой. Как все заметили, с константой в дифференциальных уравнениях можно делать практически всё, что угодно. И не всегда такие преобразования понятны новичку. Рассмотрим еще один условный пример: 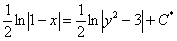. В нём целесообразно умножить все слагаемые на 2: 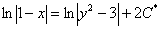. Полученная константа 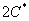– это тоже какая-то константа, которую можно обозначить через 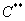: 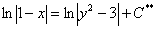. Да, и коль скоро в правой части логарифм, то константу 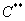целесообразно переписать в виде другой константы: .

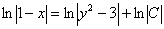Беда же состоит в том, что частенько не заморачиваются с индексами, и используют одну и ту же букву 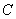. И в результате запись решения принимает следующий вид:

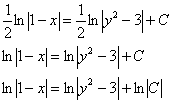
Что за фигня? Тут же ошибки. Формально – да. А неформально – ошибки нет, подразумевается, что при преобразовании константы 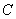всё равно получается какая-то другая константа .

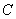Или такой пример, предположим, что в ходе решения уравнения получен общий интеграл 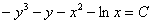. Такой ответ выглядит некрасиво, поэтому целесообразно сменить у всех множителей знаки: 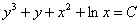. Формально по записи тут опять ошибка, следовало бы записать 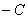. Но неформально подразумевается, что 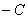– это всё равно какая-то другая константа (тем более 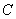может принимать любое значение), поэтому смена у константы знака не имеет никакого смысла и можно использовать одну и ту же букву .

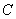Я буду стараться избегать небрежного подхода, и всё-таки проставлять у констант разные индексы при их преобразовании.

Пример 7

Решить дифференциальное уравнение 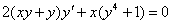. Выполнить проверку.

Решение: Данное уравнение допускает разделение переменных. Разделяем переменные:

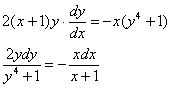
Интегрируем:

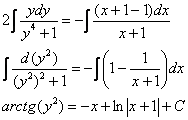
Константу 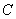тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.

Ответ: общий интеграл: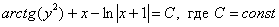

Проверка: Дифференцируем ответ (неявную функцию):

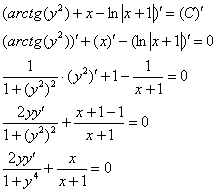
Избавляемся от дробей, для этого умножаем оба слагаемых на :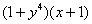

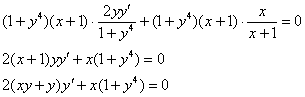
Получено исходное дифференциальное уравнение, значит, общий интеграл найден правильно.

Пример 8

Найти частное решение ДУ.
,

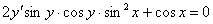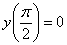
Это пример для самостоятельного решения. Единственный комментарий, здесь получится общий интеграл, и, правильнее говоря, нужно исхитриться найти не частное решение, ачастный интеграл. Полное решение и ответ в конце урока.

Как уже отмечалось, в диффурах с разделяющимися переменными нередко вырисовываются не самые простые интегралы. И вот еще парочка таких примеров для самостоятельного решения. Рекомендую всем прорешать примеры №№9-10, независимо от уровня подготовки, это позволит актуализировать навыки нахождения интегралов или восполнить пробелы в знаниях.

Пример 9

Решить дифференциальное уравнение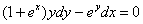

Пример 10

Решить дифференциальное уравнение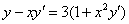

Помните, что общий интеграл можно записать не единственным способом, и внешний вид ваших ответов может отличаться от внешнего вида моих ответов. Краткий ход решения и ответы в конце урока.

Следующая рекомендуемая статья – Однородные дифференциальные уравнения первого порядка.

Успешного продвижения!

Решения и ответы:

Пример 4: Решение: Найдем общее решение. Разделяем переменные:


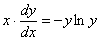
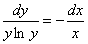
Интегрируем:



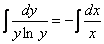
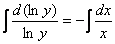
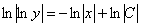
Общий интеграл получен, пытаемся его упростить. Упаковываем логарифмы и избавляемся от них:

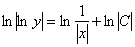
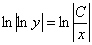
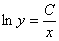
Выражаем функцию в явном виде, используя .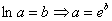
Общее решение: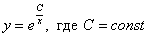

Найдем частное решение, удовлетворяющее начальному условию .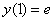
Способ первый, вместо «икса» подставляем 1, вместо «игрека» – «е»:
.
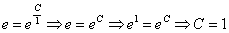Способ второй:

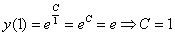
Подставляем найденное значение константы 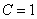в общее решение.
Ответ: частное решение: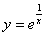

Проверка: Проверяем, действительно ли выполняется начальное условие:
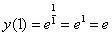, да, начальное условие 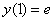выполнено.
Проверяем, удовлетворяет ли вообще частное решение 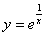дифференциальному уравнению. Сначала находим производную:

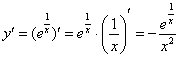
Подставим полученное частное решение 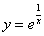и найденную производную 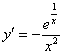в исходное уравнение :

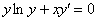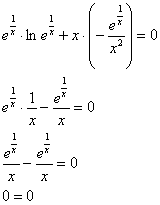
Получено верное равенство, значит, решение найдено правильно.

Пример 6: Решение: Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:




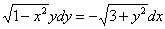
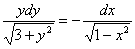
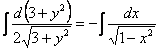
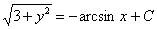
Ответ: общий интеграл: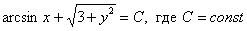

Примечание: тут можно получить и общее решение:

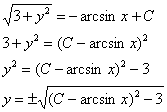
Но, согласно моему третьему техническому совету, делать это нежелательно, поскольку такой ответ смотрится довольно хреново.

Пример 8: Решение: Данное ДУ допускает разделение переменных. Разделяем переменные:



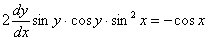
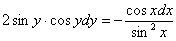
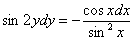
Интегрируем:


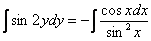
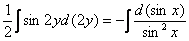
Общий интеграл: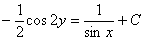
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию 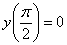. Подставляем в общее решение 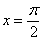и :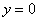

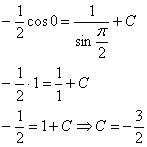
Ответ: Частный интеграл: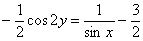
В принципе, ответ можно попричесывать и получить что-нибудь более компактное.

Пример 9: Решение: Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

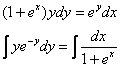
Левую часть интегрируем по частям:

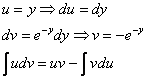
В интеграле правой части проведем замену:

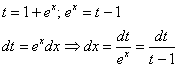
Таким образом:


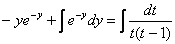
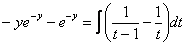
(здесь дробь раскладывается методом неопределенных коэффициентов, но она настолько простая, что подбор коэффициентов можно выполнить и устно)

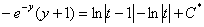
Обратная замена: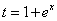



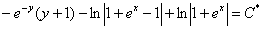
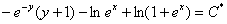
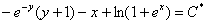
Ответ: общий интеграл: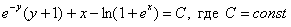

Пример 10: Решение: Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:





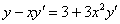
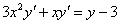
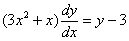
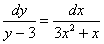
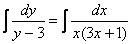
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:



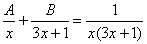
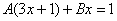
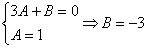
Примечание: Интеграл 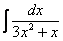можно было также найти методом выделения полного квадрата.





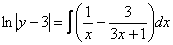
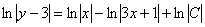
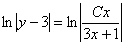
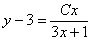
Ответ: общее решение: