Оценка погрешностей определения коэффициентов корреляции

При малых выборках, когда 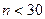стандартная ошибка определения коэффициента парной корреляции вычисляется по формуле:

.

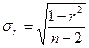Стандартная ошибка определения корреляционного отношения R, вычисляется при 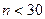по формуле:

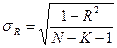, где N – число выборки, K – число факторов.

.

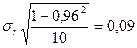Достоверность расчёта коэффициента корреляции высока.

.

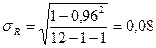Если 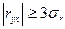, то выборочная оценка коэффициента корреляции приемлема: 0,96 > 0,27 .

В силу линейности регрессии корреляционное отношение не даёт дополнительной информации.

Коэффициент корреляции позволяет сделать вывод о целесообразности использования уравнения регрессии.

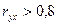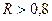Если и , то производственную функцию можно представить в форме линейной регрессии.

Для более полной оценки погрешности необходима оценка закона распределения коэффициентов корреляции.

При малом объёме выборки 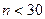и сильной корреляции 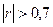закон распределения коэффициента корреляции отличается от нормального, в этом случае используется статистика Фишера.

Используя критерий достоверности t_P, определяют погрешность коэффициента кореляции и кореляционного отношения:

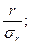t_P = t_P =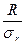

Расчётное значение критерия достоверости t_P сравниваем с фиксированным значением t_P распределения Стьюдента(n 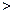50). При n 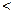30 используется статистика Фишера.

Доверительный интервал для коэффициента r₀ в генеральной совокупности определится соотношением (случай , ):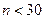

,

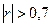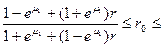
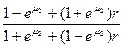где ;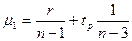

,

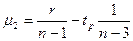t_p – находится с помощью таблиц значений функции Лапласа по уровню доверительной вероятности;

р – уровень доверительной вероятности.

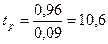
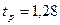
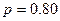
t_{p расч.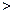} t_{p табл.}

Для ориентировочной оценки доверительных интервалов для r₀ в случае 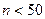, для грубых оценок доверительных интервалов можно использовать, соотношение:

.

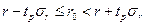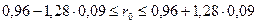
Если возьмём уровень доверительной вероятности 80% ( 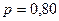), тогда значение 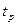из таблицы функции Лапласа будет равно ,

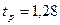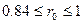
Доверительный интервал для коэффициента корреляции определится соотношением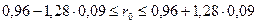

Оценка значимости представления производственной функции или оценка адекватности выбранной сглаженной зависимости 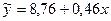реальной стохастической зависимости результата у^j от фактора 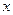^j.

Коэффициент определённости(детерминизм) для линейной регрессии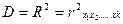

Степень влияния производственного фактора 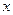^j на результат производства у^j определим на основе дисперсий отклонений сглаженных значений 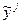от среднего наблюдаемого 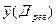и отклонений наблюдаемых величин у^j от сглаженных значений 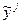, т.е. от линии регрессии (Д_ост).

Дисперсии вычисляются по формулам:

; .

; .

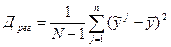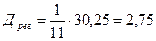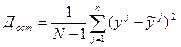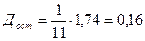Помимо указанных дисперсий вводится их сумма:

; .

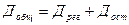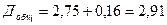Для линейной регрессии:

; .

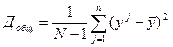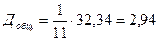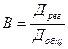, тогда .

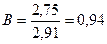Коэффициент детерминации В характеризует какая доля изменений величины у обусловлена изменением фактора х.

Величина (1-В) – характеризует долю изменений величины у от влияния неучтённых факторов. Коэффициент детерминации В=0,94 показывает, что 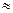90% изменений величины у вызвано изменением производственного фактора х, а (1-В)=1-0,90=0,10, т.е. 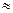10% обусловлены влиянием неучтённых факторов. В случае линейной регрессии ; ; .

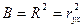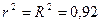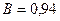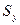- стандартное отклонение у^j от поверхности регрессии.

Выборочная оценка 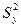дисперсии отклонения случайной величины у^j от линии регрессии 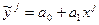равна

;

;

.

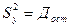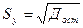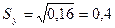Несмещённая выборочная оценка 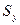стандартного отклонения величины у^j от линии регрессии составляет 0,4, т.е. находится в пределах 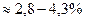от значений величины 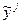, полученных из уравнения регрессии. 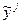изменяется (см.таблица 2) от 9,22 до 14,28, что составляет 4,3 и 2,8%:

9,22 – 100 % 14,28 – 100%

0,4 – х 0,4 –х

х=4,3% х=2,8%.

Коэффициент вариации C_у=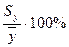

Если С_у 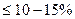, то модель адекватна действительности.