Разложение многочлена на множители

Корни многочлена.

2.2.1) Выражение вида

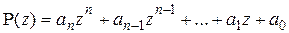
называется многочленом степени п относительно переменной z. Числа 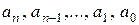называются коэффициентами многочлена, они могут быть как действительными, так и комплексными, причем старший коэффициент 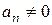. Указанный вид многочлена называется стандартным или каноническим.

2.2.2)Два многочлена

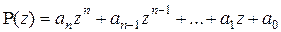и

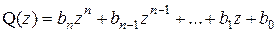
тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях переменной z:

Р(z) º Q(z) Û 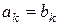, k = 0, 1, 2, ..., n.

Если 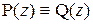, то для любого 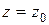выполняется равенство 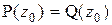, т.е. значения тождественно равных многочленов совпадают при любых значениях переменной.

2.2.3)Пусть Р(z) и Q(z) – многочлены с действительными коэффициентами, причем Q(z) не равен тождественно нулю. Тогда существуют многочлены S(z) и R(z) такие, что

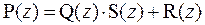, (2.1)

причем степень многочлена R(z) меньше степени многочлена Q(z). Нахождение многочленов S(z) и R(z) называется делением многочлена P(z) на многочлен Q(z) с остатком. Многочлены S(z) и R(z) в равенстве (2.1) называются соответственно частным и остатком от деления многочлена Р(z) на многочлен Q(z). Равенство (2.1) может быть записано в виде

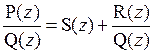. (2.2)

2.2.4)Если остаток R(z) º 0, то говорят, что многочлен Р(z) делится нацело на многочлен Q(z). Тогда имеет место равенство

.

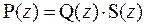В этом случае говорят также, что многочлен Р(z) разложен на множители Q(z) и S(z); многочлены Q(z) и S(z) называются делителями многочлена Р(z).

2.2.5)Теорема Безу: остаток от деления многочлена

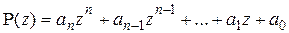
на двучлен 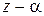равен значению многочлена Р(z) при .

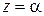Таким образом,
,
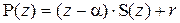где r = P(a) – число, а многочлен S(z) имеет степень 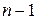, т.е. на единицу меньше степени многочлена Р(z).

2.2.6)Число a называется корнеммногочлена Р(z), если Р(a) = 0*).

При этом

,

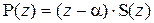причём степень многочлена S(z) на единицу меньше степени Р(z).

Если многочлен Р(z) делится без остатка на 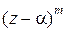, но не делится без остатка на 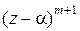, то число a является для Р(z) корнем кратности т. В этом случае имеет место равенство

,

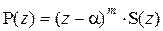где S(a) ¹ 0, а т ³ 1.

2.2.7)Из основной теоремы алгебры следует, что всякий многочлен Р(z) степени п (n ³ 2) на множестве комплексных чисел разлагается на п линейных множителей:

,

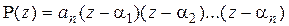где 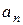– старший коэффициент, а 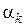, k = 1, 2, ..., n, – корни многочленаР(z).Если среди корней 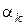есть кратные, то разложение примет вид ,

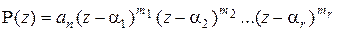где т₁, т₂, ... , т_r – кратности корней 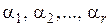соответственно,причем т₁+ т₂ + ... + т_r = п.

2.2.8)Среди многочленов с действительными коэффициентами, неразложимымина множители меньшей степени (неприводимыми), являются

только линейные многочлены вида 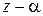и многочлены второй степени

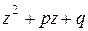
(квадратные трёхчлены), не имеющие действительных корней.

2.2.9) Если многочлен с действительными коэффициентами имеет комплексный корень 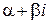, то сопряженное число 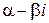также является корнем этого многочлена. Тогда выполняется равенство

.

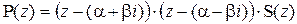Можно показать, что 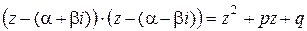, где р и q – действительные числа, а D = p² – 4q < 0.

Это означает, что если многочлен с действительными коэффициентами имеет комплексный корень, то в его разложении на неприводимые множители с действительными коэффициентами обязательно будет множитель второй степени.

2.2.10)Если несократимая дробь 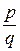является корнем многочлена с целыми коэффициентами, то число р является делителем свободного члена 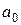, а число q – делителем старшего коэффициента 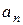. Если многочлен с целыми коэффициентами имеет целые корни, то их нужно искать среди делителей свободного члена.

2.2.11) Справедлива теорема Виета: если a₁, a₂, …, a_п – корни многочлена 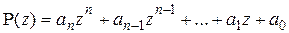, то коэффициенты этого многочлена выражаются через его корни по формулам:

а_п–1 = – (a₁+ a₂ + …+ a_п),

а_п–2 = a₁a₂ + a₁a₃ + … a₁a_п + a₂a₃ +… + a_п–1a_п,

а_п–3 = – (a₁a₂a₃ + a₁a₂a₄ + … + a_п–2a_п–1a_п),

. . . . . . . . . . . . . . . . . . . . . . . .

а₁ = (–1)^п–1(a₁a₂…a_п–1 + a₁a₂…a_п–2a_п + … + a₂a₃…a_п),

а₀ =(–1)^пa₁a₂…a_п.

Пример 2.1.1

Преобразовать многочлен к стандартному виду и найти его степень:

а) ;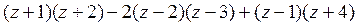

б) .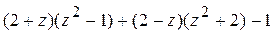

Решение

а) Раскроем скобки и приведем подобные члены:

=

= =

= = .

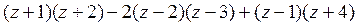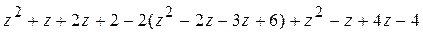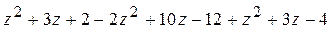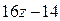Следовательно, данный многочлен есть многочлен первой степени.

б) Аналогично:

=

= = ,

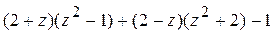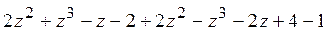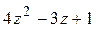Это многочлен второй степени.

Пример 2.1.2

Разделить многочлен 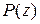на многочлен :

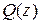а) , ;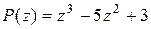

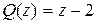б) , ;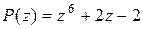

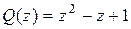в) , .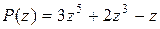

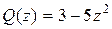Решение

а) Деление многочлена на многочлен можно выполнять «уголком» аналогично делению чисел.

В нашем случае многочлен 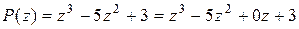это делимое, а многочлен 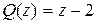– делитель. Разберем на данном примере алгоритм деления.

1. Разделим первое слагаемое делимого на первое слагаемое делителя

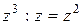( ) и поместим результат в нижней строке «уголка», под

чертой – это и будет первое слагаемое частного:

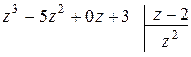
2. Умножим делитель на это первое слагаемое частного: 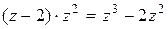. Запишем полученный многочлен под первыми слагаемыми делимого:

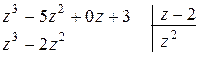
и вычтем этот многочлен из делимого

;

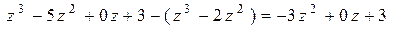результат запишем под чертой:

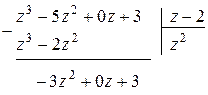
3. Повторим предыдущие шаги, используя в качестве делимого многочлен 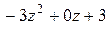, записанный под чертой. А именно:

разделим первое слагаемое ( 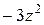) этого многочлена на первое слагаемое z делителя, получим ,

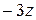прибавим этот одночлен к первому слагаемому частного (в «уголке» под чертой); умножим делитель на ( 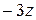) и запишем полученное выражение ( 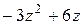) под новым делимым;

затем вычтем это выражение из многочлена 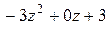и полученную разность запишем под чертой:

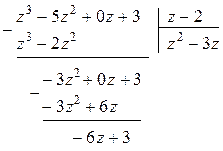
4. Повторим третий шаг, используя в качестве делимого полученный многочлен :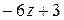

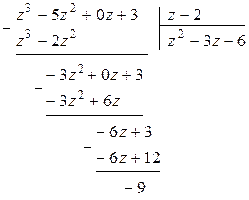
Поскольку на последнем шаге получился многочлен нулевой степени (число –9), и степень этого многочлена меньше степени делителя ( 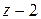), то деление закончено, а число (–9) есть остаток от деления многочлена 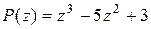на многочлен .

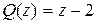Таким образом, получаем (информация 2.2.3)

,

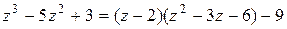или можно записать так .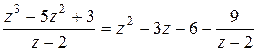

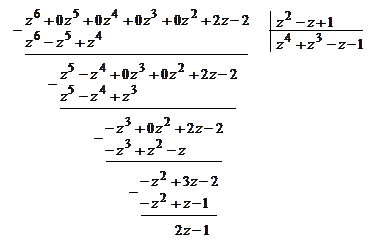б) Используя рассмотренный в пункте а) алгоритм, выполним деление многочлена 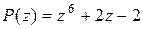на многочлен *) :

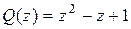Следовательно, получили неполное частное 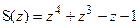и остаток 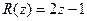. Можно записать равенство

= ( )( ) + ( )

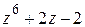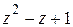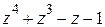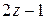или .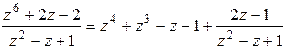

в) Разделим многочлен 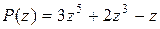на многочлен :

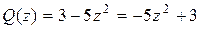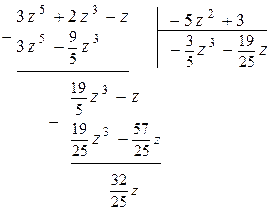
Таким образом, ,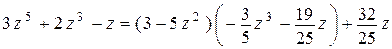

или .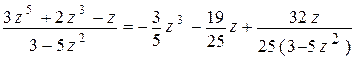

Пример 2.1.3

Многочлен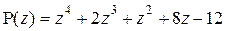

а) разложить на неприводимые множители с действительными коэффициентами;

б) разложить на линейные множители;

в) найти все корни многочлена .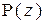

Решение

Разложение многочлена с действительными коэффициентами на множители рекомендуем проводить по алгоритму:

1. Если возможно, примените непосредственно метод группировки и вынесения общего множителя за скобки.

2. Если это не удается, найдите один из корней a подбором и, разделив заданный многочлен на z – a, представьте его в виде .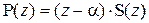

3. К многочлену S(z) примените пункты 1 и 2 данного алгоритма.

Воспользуемся этим алгоритмом при решении нашей задачи.

а) Для заданного многочлена способ группировки и вынесения общего множителя не представляется очевидным. Поэтому найдем подбором один из целых корней заданного многочлена (если он существует), используя информацию 2.2.10 . Свободный член а₀ = –12, его делителями являются числа: ±1, ±2, ±3, ±4, ±6, ±12. Чтобы проверить, является ли хотя бы одно из этих чисел корнем многочлена Р(z), нужно вычислить значения многочлена при этих значениях переменной z:

Р(–1) = 1 – 2 + 1 – 8 –12 = –20 ¹ 0,

это значит, что z = –1 не является корнем многочлена.

Р(1) = 1 + 2 +1 + 8 – 12 = 0,

следовательно, z = 1 – корень многочлена Р(z) и в разложении Р(z) имеется множитель (z – 1).

Разделим многочлен Р(z) на (z – 1):

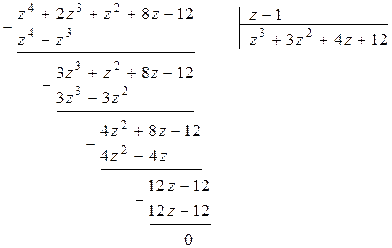
В результате имеем Р(z) = (z – 1)(z³ +3z² + 4z+12).

Теперь разложим на множители многочлен z³ +3z² + 4z +12. Для этого сгруппируем его члены и вынесем общий множитель за скобки:

z³ +3z² + 4z+12 = (z³ +3z²) + (4z +12) = z²(z + 3) + 4(z + 3) = (z + 3)(z² + 4).

Тогда можно записать разложение

Р(z) = (z – 1)(z³ +3z² + 4z+12) = (z – 1)(z + 3)(z² + 4)

Двучлен z² + 4 не имеет действительных корней:

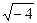
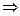z² + 4 = 0 Þ z² = – 4 z = ± z = ± 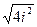Þ z = ± 2i.

Значит, на множестве действительных чисел множитель z² + 4 является неприводимым, следовательно, исходный многочлен Р(z) на множестве действительных чисел на линейные множители разложить нельзя.

Таким образом, разложение заданного многочлена на неприводимые множители на множестве действительных чисел имеет вид

Р(z) = (z – 1)(z + 3)(z² + 4).

б) Рассмотрим заданный многочлен над полем комплексных чисел. Так как двучлен 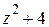имеет корни 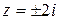, то можно записать

.

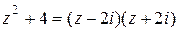Тогда имеем разложение заданного многочлена на линейные множители:

Р(z) = (z – 1)(z + 3)( z –2i)(z + 2i).

в) Три корня данного многочлена мы отыскали в процессе разложения его на множители: 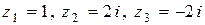. Но эти же корни можно найти, используя полученное разложение на линейные множители: произведение 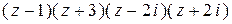тогда и только тогда равно нулю, когда равен нулю хотя бы один из сомножителей.

Отсюда получим

Р(z) =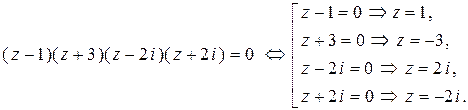

Таким образом, многочлен имеет четыре корня

.

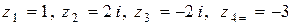Задачи «разложить многочлен на линейные множители» и «найти все корни многочлена » тождественны (эквивалентны). Действительно, если известно разложение

,

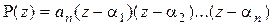то, используя утверждение «произведение тогда и только тогда равно нулю, когда равен нулю хотя бы один из сомножителей», и приравнивая поочередно каждый из сомножителей разложения нулю, найдем корни многочлена: 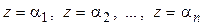. И обратно, если известны корни 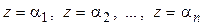многочлена, то на основании 2.2.6 можно записать

.

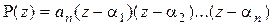2.2.12)Для сокращения записи деления многочлена на двучлен 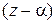удобно использовать схему Горнера. Суть ее в следующем.

Если в результате деления многочлена

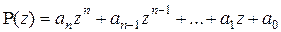
на двучлен 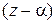получается частное

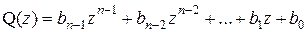
и остаток r = P(a), то коэффициенты b_k многочлена Q(z) и остаток r можно найти с помощью таблицы:

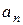		an–1	an–2	...	a1	a0
a				...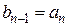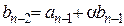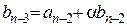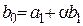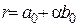

Заполняют таблицу так:

1) в первой строке этой таблицы записывают все коэффициенты многочлена Р(z) (коэффициенты при отсутствующих степенях считают равными нулю);

2) слева от второй строки таблицы записывают число a;

3) в первую клетку второй строки переносят стоящее над ней в первой клетке первой строки число ;

4)

каждая следующая клетка второй строки заполняется по правилу: содержимое предыдущей клетки умножается на число a, к произведению прибавляется число, стоящее в первой строке над заполняемой клеткой, результат записывается в заполняемую клетку:

Если в последней клетке заполняемой строки получился ноль – значит, деление выполнено нацело (без остатка), а число a является корнем заданного многочлена.

С помощью схемы Горнера легко проверить, является ли заданное число корнем рассматриваемого многочлена.

Пример 2.1.4

Найти корни многочлена 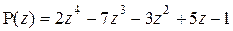и разложить его на линейные множители.

Решение

Проверим, имеет ли многочлен Р(z) целые корни. Согласно информации 2.2.10, их нужно искать среди делителей свободного члена 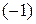данного многочлена, этими делителями являются числа ± 1. Используя схему Горнера, проверим, являются ли эти числа корнями многочлена Р(z):

		–7	–3		–1
		–5	–8	–3	–4
–1		–9		–1

Во второй строке этой таблицы проверили, является ли число 1 корнем многочлена. Так как в последней клетке этой строки получили –4 ¹ 0 , то 1 не является корнем. В третьей строке (мысленно игнорируя вторую строчку) аналогично проверили число (–1), оно является корнем заданного многочлена, т.к. в последней клетке получился 0. В этой же строке одновременно получили и коэффициенты частного от деления Р(z) на 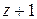, которое является многочленом третьей степени (информация 2.2.5). Тогда можно записать:

.

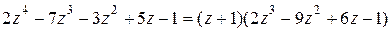Теперь найдем корни многочлена 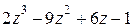. Непосредственной подстановкой легко проверить, что число (–1) корнем не является (число 1 проверять нет необходимости, так как оно не является корнем многочлена Р(z), значит, не может быть корнем и ни одного из его делителей). Так как старший коэффициент равен 2, то многочлен может иметь рациональные корни и, согласно информации 2.2.10, ими могут быть только числа ± 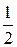. Используя схему Горнера, получим

		–9		–1
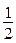–		–10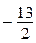
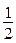		–8

Как следует из таблицы, число 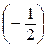не является корнем (в последней клетке второй строки не получили 0). Из третьей строки таблицы следует, что число 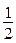есть корень заданного многочлена. Используя данные третьей строки, имеем

.

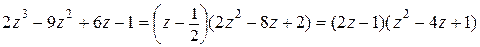Корни квадратного трехчлена 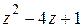можно найти обычным способом:

,

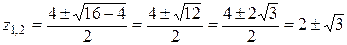откуда 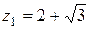и 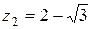, значит,

= .

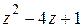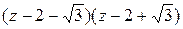Таким образом, мы нашли все четыре корня заданного многочлена:

1, , , .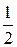

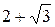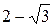Тогда разложение многочлена P(z) на линейные множители имеет вид:

.

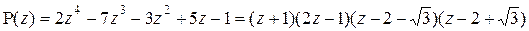Теперь предлагаем вам решить (хотя бы некоторые) приведенные ниже задачи для самостоятельного решения. А затем обязательно ответьте на вопросы теста для самоконтроля.