Правило перехода от алгебраической формы комплексного числа к тригонометрической.
Комплексные числа.
1.1 Действия над комплексными числами, заданными в алгебраической форме.
Определение. Комплексными числами называются числа вида a +bi, глее a и b – действительные числа (a 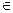 R, b
R, b 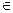 R), i-некоторое (недействительное) число квдрат которого равен -1: i
R), i-некоторое (недействительное) число квдрат которого равен -1: i 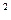 =-1.
=-1.
z=a+bi – комплексное число (в алгебраической форме)
а – действительная часть комплексного числа
bi – мнимая часть комплексного числа
b – коэффициент при мнимой части
i - мнимая единица
Числа z=a+bi и z=a-bi называются сопряженными числами.
Арифметические действия (сложение, вычитание, умножение и деление) над комплексными числами производятся как действия над обычными буквенными выражениями (одночленами и двучленами), но с учетом того, что i 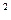 =-1
=-1
| Определение | Пример |
| Сложение | |
| (a+bi)+(c+bi)=(a+c)=(b+d)i | (2+7i)+(5-3i)=2+5+7i-3i=7+4i |
| Вычитание | |
Разность двух комплексных чисел z 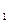 =a+bi и z =a+bi и z 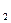 =c+di называется такое комплексное число z =c+di называется такое комплексное число z 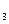 =x+yi, которое в сумме с z =x+yi, которое в сумме с z 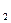 дает z дает z 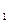 . (Из определения следует, что z . (Из определения следует, что z 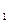 -z -z 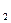 =(a-c)+(b-d)i =(a-c)+(b-d)i | (7+4i)-(5-3i)=7-5+4i+3i=2+7i (Причем (2+7i)+(5-3i)=7+4i) |
| Умножение | |
| (a+bi) (c+di)=(ac-bd)+(ad+bc)i | (2+3i)(7-4i)=14+8i+21+12i 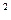 = = (заменяем i = = (заменяем i 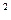 на -1)=2+29i на -1)=2+29i |
| Деление При выполнении деления комплексных чисел удобно сначала домножить числитель и знаменатель на число, сопряженное знаменателю. | |
Частным от деления двух комплексных чисел z 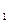 =a+bi и z =a+bi и z 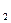 =c+di (z =c+di (z 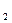 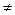 0) называется такое комплексное число z 0) называется такое комплексное число z 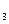 =x+yi, которое при умножении на z =x+yi, которое при умножении на z 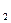 дает z дает z 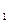 . (Из определения следует, что . (Из определения следует, что 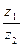 = = 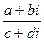 = = 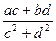 + + 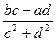 i). i). | 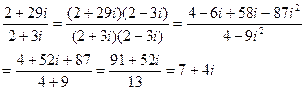 (Причем (7+4i)(2+3i)=2+29i) (Причем (7+4i)(2+3i)=2+29i) |
Нахождение числа i
Если показатель степени I делится на 4, то значение степени равно 1, если при делении показателя на 4 в остатке получается 1, то значение степени равно I, если при делении показателя на 4 остаток равен 2, то значение степени равно -1, если в остатке при делении показателя на 4 будет 3, то значение степени равно –i.
Пример 1. Вычислить: 1) 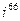 , 2)
, 2) 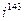 ), 3)
), 3) 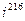 , 4)
, 4) 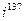
Решение:
1) 66:4=16(2). Остаток равен 2, значит 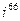 =-1,
=-1,
2) 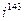
143:4=35(3). В остатке 3, значит 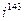 =-1.
=-1.
3) 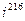
216:4=54(0). В остатке 0, значит 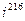 =1.
=1.
4) 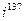
137:4=34(1). В остатке 1, значит 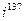 =I
=I
1.1 Упражнения для самостоятельного решения.
- Вычислить:
1) 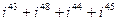 ;
;
2) 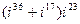 ;
;
3) 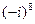 ;
;
4) 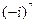 ;
;
5) 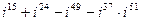 ;
;
6) 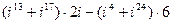 ;
;
7) 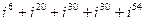 ;
;
8) 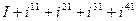 ;
;
9) 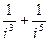 ;
;
10) 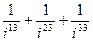
- Найти выражения
1) 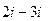 ; 23)
; 23) 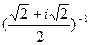 ;
;
2) 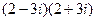 ; 24)
; 24) 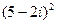 ;
;
3) 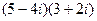 ; 25)
; 25) 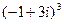 ;
;
4) 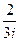 ; 26)
; 26) 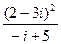 ;
;
5) 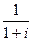 ; 27)
; 27) 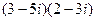 ;
;
6) 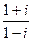 ; 28)
; 28) 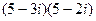 ;
;
7) 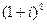 ; 29)
; 29) 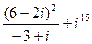 ;
;
8) 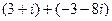 ; 30)
; 30) 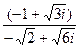 ;
;
9) 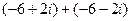 31)
31) 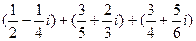 ;
;
10) 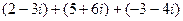 ; 32)
; 32) 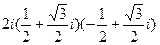 ;
;
11) 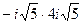 ; 33)
; 33) 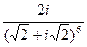 ;
;
12) 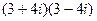 ; 34)
; 34) 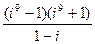 ;
;
13) 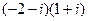 ; 35)
; 35) 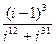 ;
;
14) 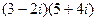 ; 36)
; 36) 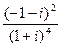 ;
;
15)  ; 37)
; 37) 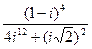 ;
;
16) 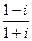 ; 38)
; 38) 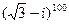
17) 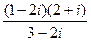 ; 39)
; 39) 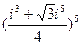 ;
;
18) 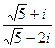 ; 40)
; 40) 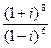 ;
;
19) 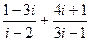 ; 41)
; 41) 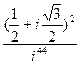
20) 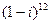 ; 42)
; 42) 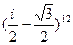 ;
;
21) 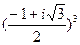 ; 43)
; 43) 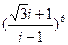
22) 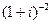 ;
;
1.2 Решение квадратных уравнений с отрицательным дискриминантом.
Пример 2. Решить квадратное уравнение
Решение:
а) 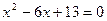 . Находим дискриминант по формуле
. Находим дискриминант по формуле 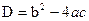 .
.
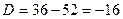
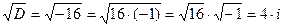 , т.к.
, т.к. 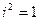 , значит
, значит 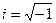
Находим корни по формуле 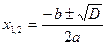
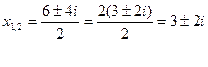
Ответ: 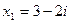 ,
, 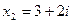 .
.
б) 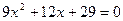
Находим дискриминант
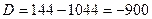
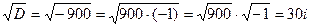
Находим корни:
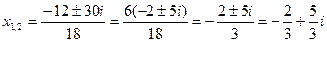
Ответ: 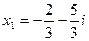 ,
, 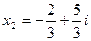
Вывод: Если дискриминант меньше 0, то квадратное уравнение имеет два сопряженных комплексных корня.
1.3 Упражнения для самостоятельного решения.
1.Решить квадратные уравнения
1) 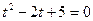
2) 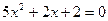
3) 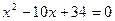
4) 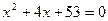
5) 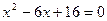
6) 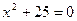
7) 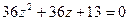
8) 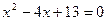
9) 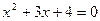
10) 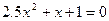
11) 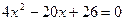
12) 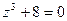
13) 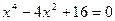
14) 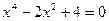
15) 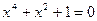
1.5 Тригонометрическая форма комплексного числа. Переход от алгебраической формы комплексного числа к тригонометрической и обратно.
Пусть комплексное число z=a+bi изображено в виде вектора 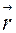 с началом 0 (0;0) и концом
с началом 0 (0;0) и концом
z (a;b) (рис.1)
Модулем комплексного числа z=a+bi называется длина вектора 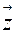 , которую можно найти по формуле:
, которую можно найти по формуле:
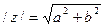
Обозначив модуль комплексного числа буквой r, получим 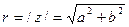 (1)
(1)
Аргументом комплексного числаназывается угол 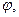 который образует вектор z с положительным направлением оси абсцисс
который образует вектор z с положительным направлением оси абсцисс 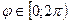 , но иногда
, но иногда 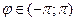 .
.
Величину угла 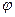 можно найти по формуле
можно найти по формуле 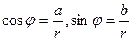 (2)
(2)
Из данных соотношений находим
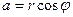 ,
, 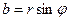
Если в запись комплексного числа zвместо a и b подставить эти значения, то получим:
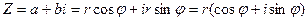 .
.
Таким образом, получаем новую форму записи комплексного числа:
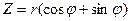 , (3)
, (3)
Которая называется тригонометрической формой комплексного числа.
Правило перехода от алгебраической формы комплексного числа к тригонометрической.
1. Находим модуль комплексного числа r по формуле 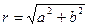
2. Для нахождения 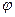 определяем, в какой четверти находится точка z.
определяем, в какой четверти находится точка z.
3. Составим уравнение 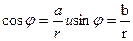
4. Запишем комплексное число в тригонометрической форме.
Пример 3. Записать в тригонометрической форме число 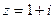
Решение:
1. Так как 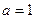 ,
, 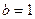 , то
, то 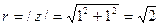 .
.
2. Изобразим число z геометрически
Видим, что числу z соответствует точка z, лежащая в I четверти и вектор 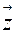 .
.
3. Составим отношения 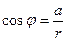 и
и 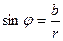 т.е.
т.е.
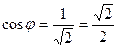 ,
, 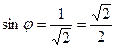
Этим соотношением соответствует в I четверти угол 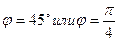 .
.
4. Так как 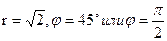 , то тригонометрическая форма заданного комплексного числа имеет вид
, то тригонометрическая форма заданного комплексного числа имеет вид 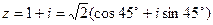 или
или
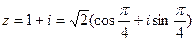 .
.
Пример 4. Записать число 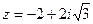 в тригонометрической форме.
в тригонометрической форме.
Решение:
1. Здесь 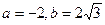 , следовательно
, следовательно
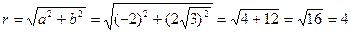
Изобразим число z геометрически
Видим, что числу z соответствует точкаz, лежащая во II четверти, и вектор 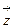 .
.
2. Находим 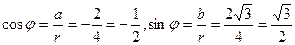 .
.
Этим соотношениям соответствует угол 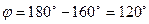
или 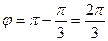
3. Запишем заданное число в тригонометрической форме:
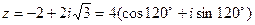
или 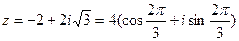 .
.
Пример 5. Записать в тригонометрической форме чисто мнимое число 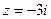
Решение:
1. Запишем данное число в виде 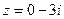 . Значит,
. Значит, 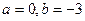 , откуда
, откуда
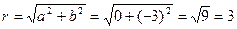
Точка соответствует геометрическому числу 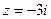 , лежит на мнимой оси
, лежит на мнимой оси
2. Аргумент этого числа равен 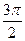 , так как угол отсчитывается от положительного направления оси ОХ против часовой стрелки.
, так как угол отсчитывается от положительного направления оси ОХ против часовой стрелки.
4. Запишем заданное число в тригонометрической форме:
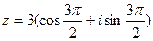
Пример 6. Записать число 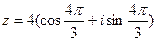 в алгебраической форме.
в алгебраической форме.
Решение: Так как аргумент 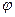 этого числа равен
этого числа равен 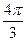 , то числу z соответствует на комплексной плоскости точка, расположенная в III четверти. Используя формулы приведения, находим
, то числу z соответствует на комплексной плоскости точка, расположенная в III четверти. Используя формулы приведения, находим
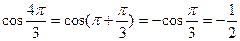 ,
,
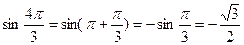 .
.
Подставим в тригонометрическую форму числа полученные значения и раскроем скобки:
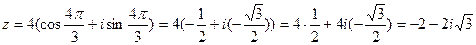 .
.
Итак, алгебраическая форма данного числа имеет вид
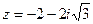
Пример7. Извлечь корень 4-ой степени 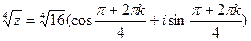 , где
, где 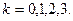 Соответственно получим
Соответственно получим
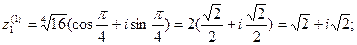
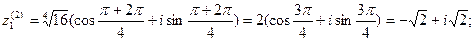
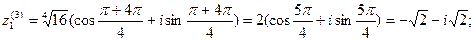
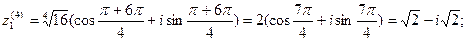
1.8 Упражнения для самостоятельного решения.
1. Найти произведение комплексных чисел 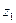 и
и 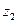
1) 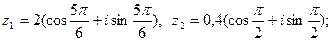
2) 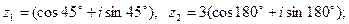

3) 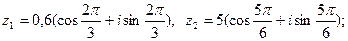
4) 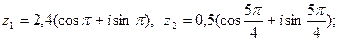
5) 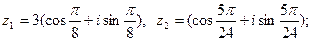
6) 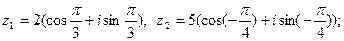
7) 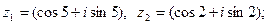
8) 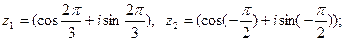
9) 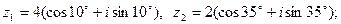
2. Найти частное комплексных чисел 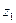 и
и 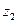
1) 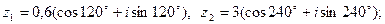
2) 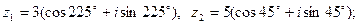
3) 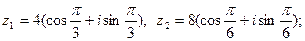
4) 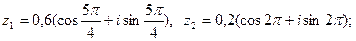
5) 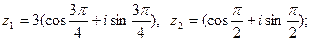
6) 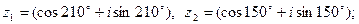
7) 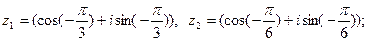
8) 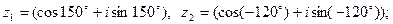
3. Произвести действия, предварительно записав комплексные числа в тригонометрической форме:
1) Найти 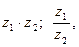 если
если 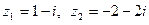
2) Найти 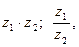 если
если 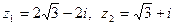
3) Найти 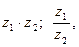 если
если 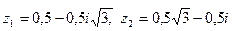
4) Найти 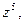 если
если 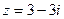
5) Найти 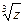 , если
, если 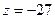
6) Найти 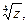 если
если 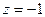
7) Найти 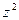 , если
, если 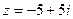
4. Даны комплексные числа. Произвести необходимые действия.
1) Дано: 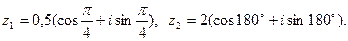
Найти: а) 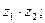 б)
б) 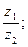 в)
в) 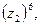 г)
г) 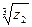
2) Дано: 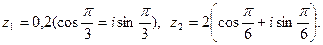
Найти: а) 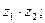 б)
б) 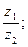 в)
в)  г)
г) 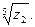
3) Дано: 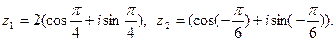
Найти: а) 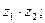 б)
б) 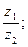 в)
в) 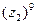 ; г)
; г) 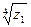 .
.
4) Дано: 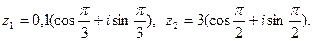
Найти: а) 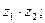 б)
б) 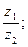 в)
в) 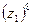 ; г)
; г) 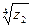 .
.
5) Дано: 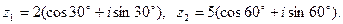
Найти: а) 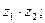 б)
б) 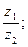 в)
в) 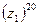 г)
г) 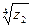
6) Дано: 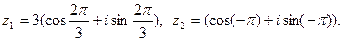
Найти: а) 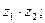 б)
б) 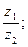 в)
в) 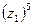 г)
г) 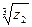 .
.
5. Извлеките корни
1) 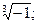 2)
2) 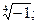 3)
3) 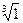 4)
4) 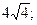 5)
5) 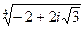 6)
6) 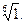
1.8. Показательная форма комплексного числа. Формула Эйлера. Переход от алгебраической формы комплексного числа к показательной и обратно.
Если комплексному числу 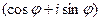 , модуль которого равен 1, поставить в соотвествие показанное выражение
, модуль которого равен 1, поставить в соотвествие показанное выражение 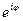 , то получим соотношение
, то получим соотношение 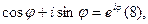 то получим соотношение которое называется формулой Эйлера.
то получим соотношение которое называется формулой Эйлера.
Любое комплексное число 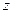 можно записать в виде
можно записать в виде 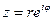 . Эта форма записи комплексного числа называется показательной формой.
. Эта форма записи комплексного числа называется показательной формой.
Пример 1. Записать число 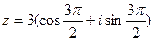 в показательной форме.
в показательной форме.
Решение.
Здесь 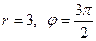 . Следовательно, показательная форма числа имеет вид
. Следовательно, показательная форма числа имеет вид 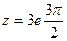 .
.
Пример 14. Записать число 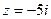 в показательной форме.
в показательной форме.
Решение. Что бы представить число 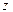 в виде
в виде 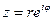 , нужно найти модуль и аргумент числа
, нужно найти модуль и аргумент числа 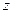 .
.
Здесь 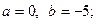 тогда
тогда 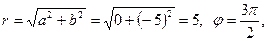 так как точка
так как точка 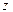 лежит на мнимой оси комплексной плоскости. Зная
лежит на мнимой оси комплексной плоскости. Зная 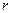 и
и 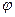 , получим
, получим 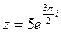 .
.
Пример 2. Записать число 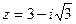 в тригонометрической и показательной формах.
в тригонометрической и показательной формах.
Решение.
Так как 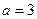 ,
, 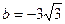 , то
, то 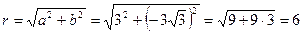
Геометрически определяем, что число z соответствует точка z, лежащая в IV четверти (рис.5)
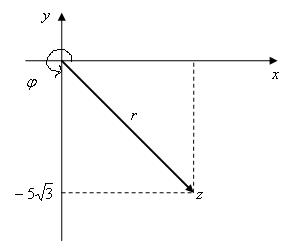
Рис.5
Составим соотношения
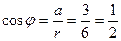 ,
,
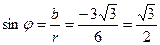
Отсюда следует, что 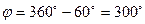
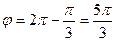 . Итак,
. Итак, 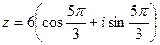 -тригонометрическая форма, а
-тригонометрическая форма, а 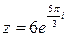 - показательная форма данного числа.
- показательная форма данного числа.
Пример 3. Записать число 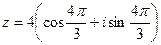 в алгебраической и показательной формах.
в алгебраической и показательной формах.
Решение.
Так как аргумент 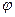 данного числа равен
данного числа равен 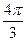 , то число
, то число 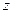 соответствует на комплексной плоскости точка, расположенная в III четверти. Используя формулы приведения, находим
соответствует на комплексной плоскости точка, расположенная в III четверти. Используя формулы приведения, находим
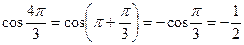 ,
,
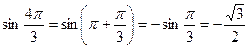
Поставим в тригонометрическую форму полученные значения и раскроем скобки:
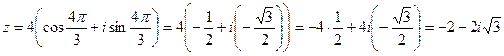
Итак, алгебраическая форма данного числа имеет вид 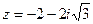 , а показательная – вид
, а показательная – вид 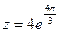 .
.
Упражнения для самостоятельного решения.
1) z = 6i; 2) z = -5; 3) z = -2-2i; 4) z = 1+i; 5) z = 1-i; 6) z = -3 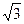 +3i;
+3i;
7) z = 2i; 8) z = -1+i; 9) z = 1-i 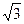 .
.
2. Записать комплексные числа в алгебраической и показательной формах:
1) 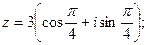
2) 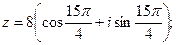
3) 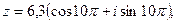
4) 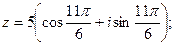
5) 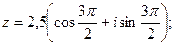
6) 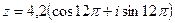 ;
;
3. Записать комплексные числа в алгебраической и тригонометрической формах.
1) z = 2,6 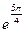 ; 2) z = 4
; 2) z = 4 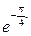 3) z = 1,8
3) z = 1,8 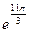 ; 4) z = 5
; 4) z = 5 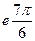 ; 5) z = 2,4
; 5) z = 2,4 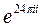
6) z = 8,2 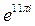
1.10. Действия над комплексными числами, заданными в показательной форме.
Если комплексные числа записаны в показательной форме, то умножение, деление, возведение в степень производится по правилам действий со степенями.
Так, для произведения и частного комплексных чисел 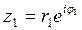 и
и 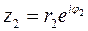 справедливы формулы
справедливы формулы
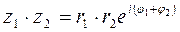 , (9)
, (9)
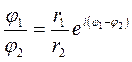 , (10)
, (10)
а для n-й степени комплексного числа 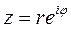 - формула
- формула 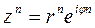 (11)
(11)
Для вычисления корня из комплексного числа 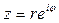 используется формула
используется формула
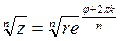 , (12)
, (12)
Где k принимает n значений: 0,1,2,…,n-1.
Пример 1. Представить числа 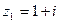 и
и 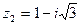 в показательной форме, вычислить:
в показательной форме, вычислить:
1) 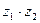 ; 2)
; 2) 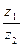 3)
3) 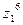 ; 4)
; 4) 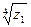
Решение.
Для числа z1=1+I имеем: а = 1, b =1, тогда 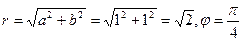 , так как точка z лежит в I четверти, т.е.
, так как точка z лежит в I четверти, т.е. 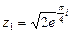 .
.
Для числа 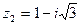 имеем:
имеем: 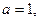
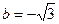
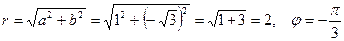 , т.е.
, т.е. 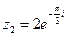
1) По формуле (9) находим
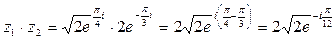
2) По формуле (10) получим
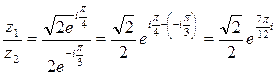
3) По формуле (11) имеем
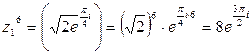
4) По формуле (12) находим
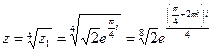 , к = 0,1,2,3;
, к = 0,1,2,3;
Если к = 0, то 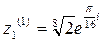 ;
;
Если к = 1, то 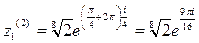
Если к = 2, то 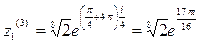
Если к = 3, то 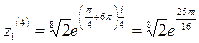
Пример 2. Записать в показательной форме комплексное число
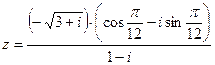
Решение. Запишем данное число в виде
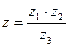 , где
, где 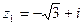 ,
,
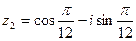 ,
,
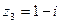
Каждое из чисел 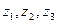 представим в показательной форме
представим в показательной форме
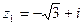 , здесь
, здесь 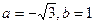 , находим
, находим 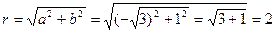
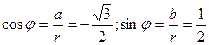 , тогда
, тогда 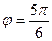 .
.
Получаем 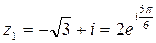
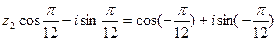 , здесь
, здесь 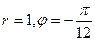 , тогда
, тогда 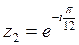 ,
,
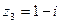 , здесь
, здесь 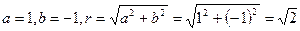 ,
,
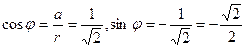 , тогда
, тогда 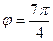 .
.
Получаем 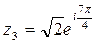
Итак,
Пример. Для извлечения квадратного корня из числа 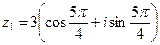 воспользуемся формулой
воспользуемся формулой 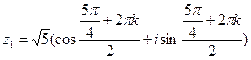 , где
, где 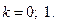
При 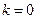 получим
получим
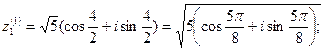
при 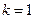 получим
получим
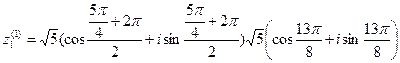
Пример. Найти 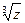 , если
, если 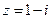
Решение. Запишем комплексное число z в тригонометрической форме. Найдем
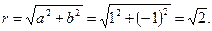
Поскольку 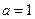 и
и 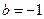 , точка, соответствующая этому числу, расположена в IV четверти.
, точка, соответствующая этому числу, расположена в IV четверти.
Составим соотношения
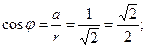
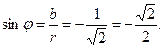
Учитывая, что точка z расположена в IV четверти, находим 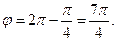
Теперь воспользуемся формулой 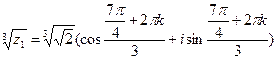 где
где 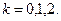
Тогда получим:
Если 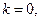 то
то
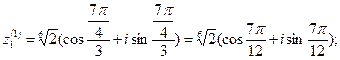
Если  , то
, то
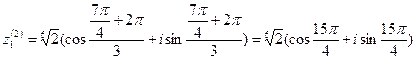
Если 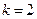 ,то
,то
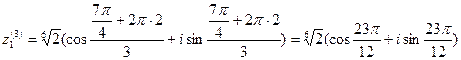
Пример. Найти 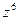 , если
, если 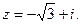
Решение:
Запишем число z в тригонометрической форме, учитывается, что 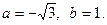 Найдем
Найдем
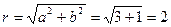
Точка z расположена во II четверти. Составим соотношения
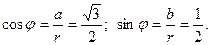
Учитывая, что точка z расположена во II четверти, находим 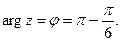
Следовательно, 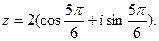
Согласно формуле возведения в степень, имеем
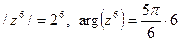 и, значит
и, значит
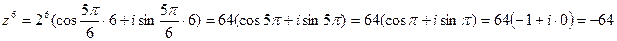
Упражнения для самостоятельного решения.
- Представить в показательной форме числа:
1) 1; 2) 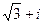 ; 3) 3+
; 3) 3+ 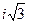 ; 4)
; 4) 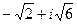
- Представив числа
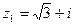 и
и 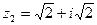 в показательной форме, вычислите:
в показательной форме, вычислите:
1) 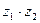 ; 2)
; 2) 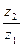 ; 3)
; 3) 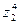 ; 4)
; 4) 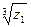 5)
5) 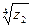
3. Найдите в показательной форме: 1) 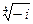 ; 2)
; 2) 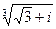
4. Найдите 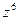 в показательной форме, если
в показательной форме, если 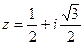 .
.
5. Запишите в показательной и алгебраической формах комплексное число:
1) 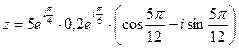 ;
;
2) 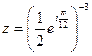 ;
;
3) 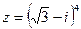 ;
;
4) 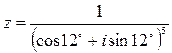 ;
;
5) 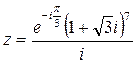 .
.
