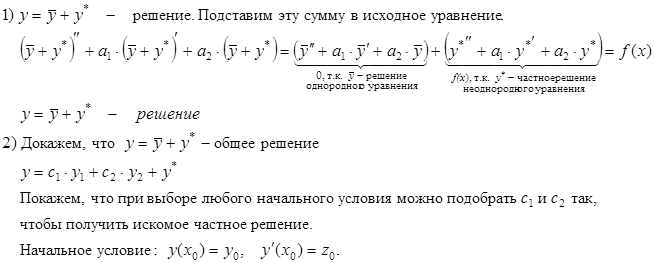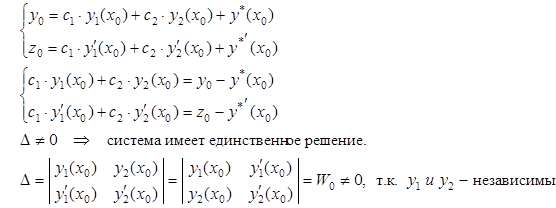Линейные однородные уравнения с постоянными коэффициентами

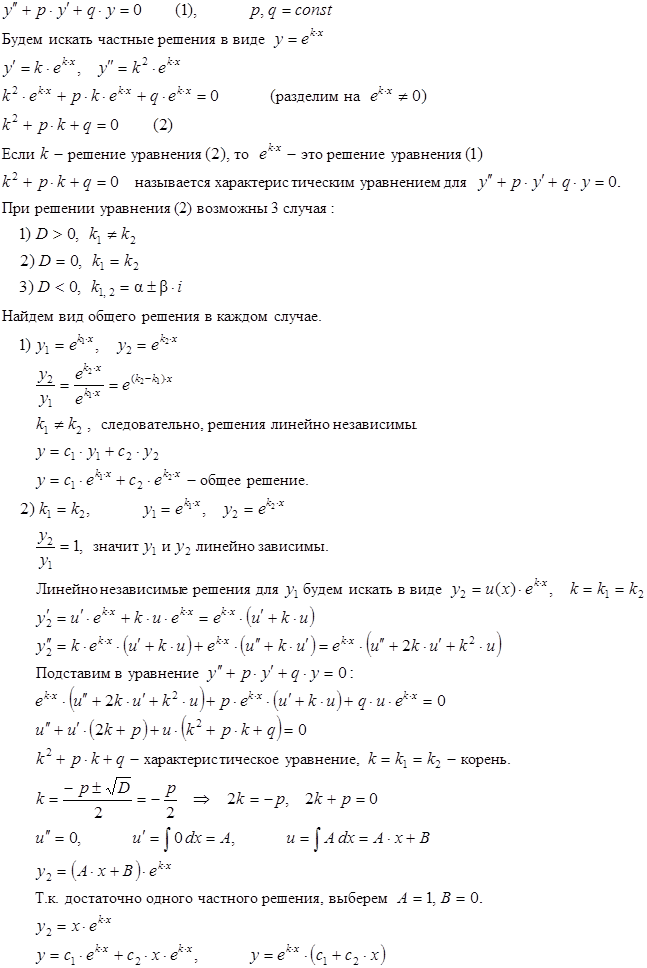
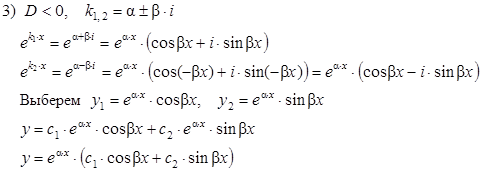
Итак:

k1,2	Частные решения	Общие решения
D > 0, k1 ¹ k2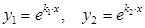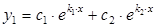
D = 0, k1 = k2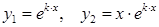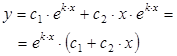
D < 0, k1,2 = a ± b×i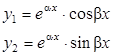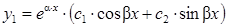

Пример:

1) Найти общее решение уравнения.

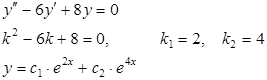
2) Найти общее решение уравнения.

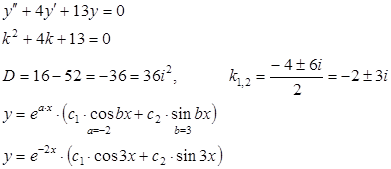
ОПРЕДЕЛЕНИЕ: Если равенство a₁×y₁ + a₂×y₂ + … + a_n×y_n = 0 выполняется только в том случае, когда a₁ = a₂ = … a_n = 0, то функции y₁, y₂, …, y_n называются линейно независимыми.

ТЕОРЕМА: Если функции y₁, y₂, …, y_n – линейно независимые решения уравнения a₁×y⁽ⁿ⁾ + a₂×y^(n–1) + a_n×y = 0, то его общее решение имеет вид y = c₁×y₁ + c₂×y₂ + … + c_n×y_n.

Пример:

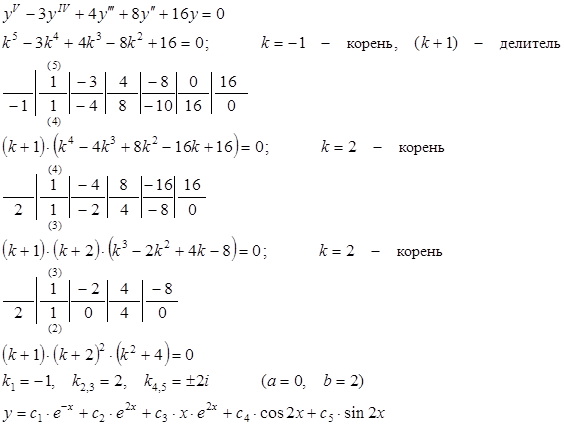
Неоднородные линейные уравнения второго порядка с постоянными коэффициентами.

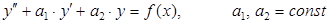
ТЕОРЕМА о структуре общего решения линейного неоднородного уравнения с постоянными коэффициентами: Общее решение y можно представить как сумму 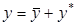, где 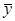– общее решение соответствующего однородного уравнения

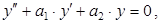
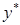– частное решение исходного неоднородного уравнения.

Доказательство.