Признак Лейбница сходимости знакочередующегося ряда
Знакочередующийся ряд сходится, если выполнены следующие два условия:
- абсолютные значения его членов представляют собой убывающую последовательность
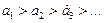 ;
;
2. предел последовательности модулей членов ряда равен нулю: 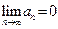 .
.
Замечание. Ошибка при замене суммы сходящегося знакочередующегося ряда суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.
4.8). Исследовать на сходимость ряд 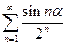 .
.
Для этого знакопеременного ряда составим ряд из абсолютных величин его членов  .
.
Это знакоположительный ряд. Сравним его с рядом 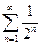 . Так как
. Так как 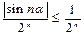 , то по первому признаку сравнения для знакоположительных рядов из сходимости ряда
, то по первому признаку сравнения для знакоположительных рядов из сходимости ряда 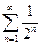 (как суммы бесконечно убывающей геометрической прогрессии со знаменателем
(как суммы бесконечно убывающей геометрической прогрессии со знаменателем 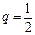 ) следует сходимость ряда
) следует сходимость ряда  . Таким образом, рассматриваемый в этом примере ряд абсолютно сходится.
. Таким образом, рассматриваемый в этом примере ряд абсолютно сходится.
4.9). Исследовать на сходимость и абсолютную сходимость ряд
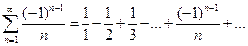 .
.
Для этого знакочередующегося ряда выполнены оба условия признака Лейбница.
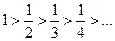 ;
;  .
.
Поэтому он сходится. Но ряд, составленный из абсолютных величин его членов,
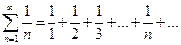
является гармоническим, и, как было показано в примере 4.6), – расходится.
Итак, рассматриваемый в этом примере ряд не является абсолютно сходящимся и потому должен быть назван условно сходящимся.
Задания для самостоятельного решения.
Исследовать следующие ряды на сходимость, проверив выполнение необходимого условия сходимости, и привлекая, если это понадобится, другие признаки сходимости.
4.1. 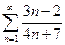 . 4.2.
. 4.2. 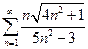 . 4.3.
. 4.3. 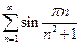 . 4.4.
. 4.4.  . 4.5.
. 4.5. 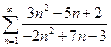 .
.
Исследовать ряды на сходимость с помощью признаков сравнения.
4.6. 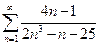 . 4.7.
. 4.7. 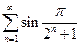 . 4.8.
. 4.8.  . 4.9.
. 4.9. 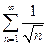 . 4.10.
. 4.10. 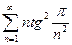
Исследовать сходимость рядов с помощью признака Даламбера.
4.11. 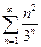 . 4.12.
. 4.12. 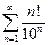 . 4.13.
. 4.13. 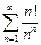 . 4.14.
. 4.14. 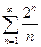 . 4.15.
. 4.15. 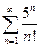 .
.
Исследовать сходимость рядов с помощью радикального признака.
4.16.  . 4.17.
. 4.17. 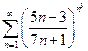 . 4.18.
. 4.18. 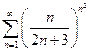 . 4.19.
. 4.19. 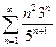 . 4.20 .
. 4.20 . 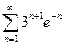 .
.
Исследовать сходимость рядов с помощью интегрального признака сходимости Коши.
4.21. 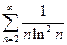 . 4.22.
. 4.22. 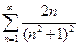 . 4.23.
. 4.23.  . 4.24.
. 4.24. 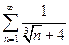 . 4.25.
. 4.25. 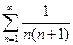 .
.
Выяснить какие из следующих рядов являются сходящимися. Для сходящихся рядов определить, сходятся они абсолютно или условно.
4.26. 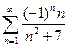 . 4.27.
. 4.27. 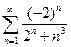 . 4.28.
. 4.28. 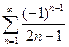 . 4.29.
. 4.29. 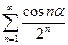 . 4.30.
. 4.30. 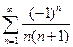 .
.
Ответы.
4.1. расходится. 4.2. расходится . 4.3. расходится. 4.4. расходится. 4.5. расходится.
4.6. сходится. 4.7. сходится. 4.8. сходится. 4.9. расходится. 4.10. сходится.
4.11. сходится. 4.12. расходится. 4.13. сходится. 4.14. расходится. 4.15. сходится.
4.16. расходится. 4.17. сходится. 4.18. сходится. 4.19. сходится. 4.20. расходится.
4.21. сходится. 4.22. сходится. 4.23. сходится. 4.24. расходится. 4.25. сходится.
4.26. сходится условно. 4.27. расходится. 4.28. сходится условно. 4.29. сходится абсолютно.
4.30. сходится абсолютно.
4.2.Функциональные ряды.
Ряд
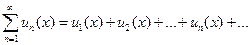 , (4.12)
, (4.12)
членами которого являются функции 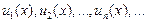 называется функциональным рядом.
называется функциональным рядом.
Если ряд (4.12) сходится при 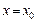 , то
, то 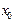 называется точкой сходимости, если же при
называется точкой сходимости, если же при 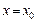 этот ряд расходится, то
этот ряд расходится, то 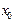 - точка расходимости. Совокупность всех точек сходимости функционального ряда называется областью его сходимости. Составим
- точка расходимости. Совокупность всех точек сходимости функционального ряда называется областью его сходимости. Составим 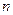 - ую частичную сумму ряда (4.12)
- ую частичную сумму ряда (4.12)
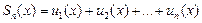 .
.
Для
 из области сходимости данного ряда существует конечный предел последовательности частичных сумм:
из области сходимости данного ряда существует конечный предел последовательности частичных сумм: 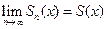 . В точках, не принадлежащих области сходимости, эта последовательность не имеет конечного предела.
. В точках, не принадлежащих области сходимости, эта последовательность не имеет конечного предела.
Степенные ряды.
Степенным рядомназывается функциональный ряд
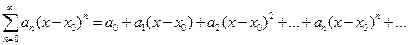 , (4.13)
, (4.13)
члены которого степенные функции. Числа 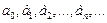 называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
В частности, если 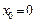 , то получим степенной ряд по степеням
, то получим степенной ряд по степеням  :
:
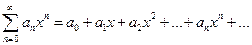 (4.14)
(4.14)
Теорема Абеля.Если степенной ряд (4.14) сходится в точке 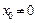 , то он сходится и притом абсолютно в интервале
, то он сходится и притом абсолютно в интервале  , т.е. для любого
, т.е. для любого  из этого интервала.
из этого интервала.
Следствие. Если степенной ряд (4.14) расходится при 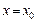 , то он расходится и для всякого
, то он расходится и для всякого  такого, что
такого, что 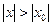 .
.
Область сходимости степенного ряда– интервал 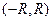 , для всех
, для всех 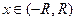 ряд сходится, причем абсолютно, для всех
ряд сходится, причем абсолютно, для всех  вне этого интервала
вне этого интервала 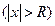 ряд расходится, при
ряд расходится, при 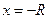 или при
или при 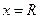 ряд может быть как сходящимся, так и расходящимся. Число
ряд может быть как сходящимся, так и расходящимся. Число 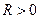 , ограничивающее интервал сходимости, называется радиусом сходимости степенного ряда.
, ограничивающее интервал сходимости, называется радиусом сходимости степенного ряда.
Если 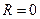 , то область сходимости состоит только из одной точки
, то область сходимости состоит только из одной точки 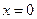 , т.е. ряд расходится для всех значений
, т.е. ряд расходится для всех значений  отличных от нуля.
отличных от нуля.
Если 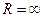 , то область сходимости – это вся ось
, то область сходимости – это вся ось 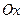 , т.е. ряд сходится при всех
, т.е. ряд сходится при всех  .
.
Для вычисления радиуса сходимости степенного ряда используются формулы Даламбера и Коши
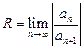 и
и 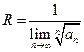 , (4.15)
, (4.15)
при условии, что указанные пределы существуют.
Для степенных рядов вида (4.13) центр интервала сходимости в точке 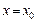 , т.е. это интервал
, т.е. это интервал 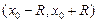 .
.
4.10). Определить область сходимости ряда  .
.
По первой из формул (4.15), формуле Даламбера, 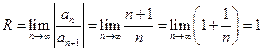 .
.
Интервал сходимости этого ряда 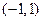 . При
. При 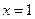 данный степенной ряд становится числовым знакоположительным
данный степенной ряд становится числовым знакоположительным 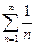 , называемым гармонический. Как было показано в примере 4.6), он расходится. При
, называемым гармонический. Как было показано в примере 4.6), он расходится. При 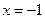 получаем знакочередующийся ряд
получаем знакочередующийся ряд 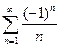 , который сходится (см. пример 4.9)). Итак, область сходимости данного степенного ряда
, который сходится (см. пример 4.9)). Итак, область сходимости данного степенного ряда 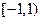 . А для любого
. А для любого 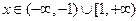 этот ряд расходится.
этот ряд расходится.
4.11). Определить область сходимости ряда 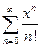 .
.
По формуле Даламбера 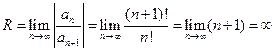 . Значит область сходимости данного ряда
. Значит область сходимости данного ряда 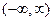 , т.е. он сходится для любого
, т.е. он сходится для любого  .
.
4.12). Определить область сходимости ряда 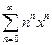 . По формуле Коши, второй из формул (4.15),
. По формуле Коши, второй из формул (4.15), 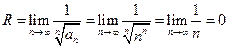 . Т.е.
. Т.е. 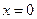 - единственная точка сходимости ряда. для всех остальных
- единственная точка сходимости ряда. для всех остальных  ряд расходится.
ряд расходится.
Разложение функции в степенной ряд.
Сумма степенного ряда
 (4.16)
(4.16)
представляет собой функцию, определенную в интервале сходимости 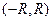 этого ряда,
этого ряда, 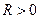 . Равенство (4.16) в этом случае называется разложением функции
. Равенство (4.16) в этом случае называется разложением функции 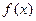 в степенной ряд на интервале
в степенной ряд на интервале 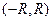 .
.
Можно показать, что функция 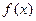 дифференцируема и ее производная
дифференцируема и ее производная 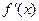 может быть представлена рядом
может быть представлена рядом
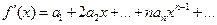 , (4.17)
, (4.17)
получаемым из ряда (4.16) его почленным дифференцированием при 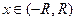 .
.
Аналогично, обе части равенства (4.16), обозначив в нем предварительно 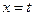 и умножив обе его части на
и умножив обе его части на 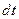 , можно проинтегрировать по
, можно проинтегрировать по 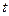 в промежутке от 0 до
в промежутке от 0 до  . В результате получим ряд
. В результате получим ряд
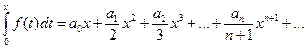 , (4.18)
, (4.18)
где 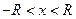 .
.
Таким образом, разложение (4.16) функции в степенной ряд допускает почленное дифференцирование и интегрирование с сохранением интервала сходимости.
Разложение данной функции 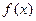 в степенной ряд позволяет вычислять значения этой функции с любой степенью точности.
в степенной ряд позволяет вычислять значения этой функции с любой степенью точности.
Простейший пример такого разложения для функции 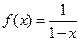 следует из формулы (4.4) суммы бесконечно убывающей геометрической прогрессии при
следует из формулы (4.4) суммы бесконечно убывающей геометрической прогрессии при 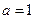 и
и 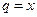
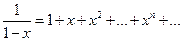 (4.19)
(4.19)
для 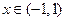 .
.
Обозначая в разложении (4.19) 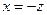 , имеем
, имеем
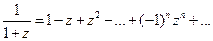 ,
,
где  . Умножая последнее равенство на
. Умножая последнее равенство на 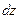 и интегрируя его почленно по
и интегрируя его почленно по 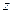 в промежутке от
в промежутке от 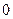 до
до  , получаем
, получаем
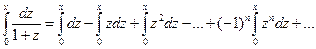 ,
,
или
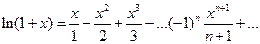 , (4.20)
, (4.20)
где  . Полученный ряд (4.20) является разложением функции
. Полученный ряд (4.20) является разложением функции 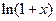 по степеням
по степеням  . При
. При 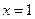 получаем
получаем 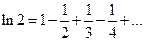 , т.е. сходящийся ряд. Поэтому область сходимости ряда (4.20)
, т.е. сходящийся ряд. Поэтому область сходимости ряда (4.20) 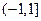 .
.
Положим в равенстве (4.19) 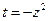
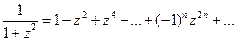 .
.
Умножая последнее равенство на 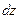 и интегрируя его по
и интегрируя его по 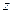 в промежутке от
в промежутке от 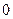 до
до  (
(  ), получим
), получим
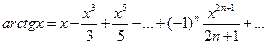 (4.21)
(4.21)
Это разложение справедливо также при 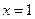 , поскольку ряд
, поскольку ряд
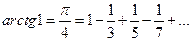 (4.22)
(4.22)
сходится. Аналогично можно показать, что ряд (4.21) сходится и при 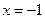 . Таким образом, разложение (4.21) функции
. Таким образом, разложение (4.21) функции 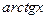 в ряд по степеням
в ряд по степеням  справедливо при
справедливо при 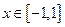 .
.
Заметим, что знакочередующийся ряд (4.22) позволяет получить значение числа 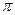 с любой степенью точности.
с любой степенью точности.
Ряд Маклорена.
Предположим, что функция 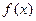 может быть разложена в степенной ряд
может быть разложена в степенной ряд
 (4.23)
(4.23)
где 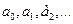 - неопределенные коэффициенты, и
- неопределенные коэффициенты, и 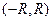 - интервал сходимости,
- интервал сходимости, 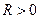 .
.
Как было указано выше, степенной ряд (4.23) можно дифференцировать почленно любое число раз, т.е.
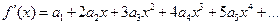 ,
,
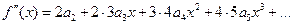 ,
,
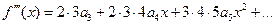 ,
,
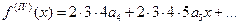 ,
,
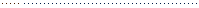
Полагая в этих равенствах и в (4.23) 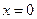 , получим
, получим 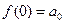 ,
, 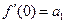 ,
, 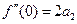 ,
, 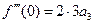 ,
, 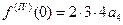 , …. Отсюда
, …. Отсюда
 .
.
Подставляя полученные значения коэффициентов 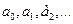 в ряд (4.23), получим ряд Маклорена
в ряд (4.23), получим ряд Маклорена
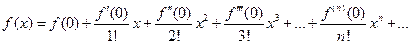 , (4.24)
, (4.24)
позволяющий любую бесконечно дифференцируемую функцию 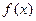 разложить в ряд по степеням
разложить в ряд по степеням  .
.
Для функций 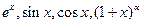 , где
, где 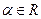 , разложения в ряд Маклорена выглядят так
, разложения в ряд Маклорена выглядят так
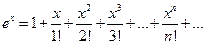 ,
, 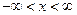 ,
,
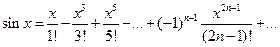 ,
, 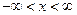 ,
,
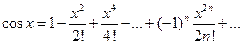 ,
, 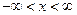 .
.
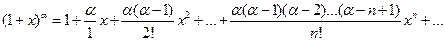 ,
, 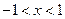 .
.
Приведенные выше разложения позволяют вычислять приближенно значения функций, определенные интегралы, и. т. п..
4.13) Например, полагая 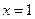 в разложении для
в разложении для  , вычислим
, вычислим 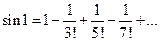 . Отбросив в этом ряду все члены, начиная с четвертого, получим приближенное значение
. Отбросив в этом ряду все члены, начиная с четвертого, получим приближенное значение
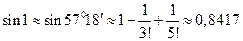 .
.
Погрешность 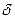 этого приближения меньше первого из отброшенных членов ряда
этого приближения меньше первого из отброшенных членов ряда 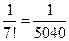 . Т.е. приближенное значение
. Т.е. приближенное значение 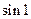 мы получили с точностью до
мы получили с точностью до 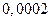 .
.
4.14) Вычислим 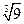 . Представим искомое число в виде
. Представим искомое число в виде 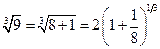 . Пользуясь разложением функции
. Пользуясь разложением функции  , и полагая в нем
, и полагая в нем 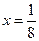 и
и 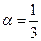 , имеем
, имеем
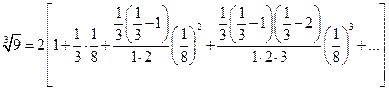
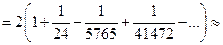
 .
.
4.15) Вычислим определенный интеграл 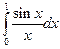 . Соответствующий неопределенный интеграл
. Соответствующий неопределенный интеграл 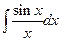 не может быть выражен в элементарных функциях, т.е. относится к так называемым “неберущимся интегралам”. Поэтому применить формулу Ньютона-Лейбница к данному интегралу нельзя. Получим его приближенное значение с помощью рядов. Разделив почленно ряд для
не может быть выражен в элементарных функциях, т.е. относится к так называемым “неберущимся интегралам”. Поэтому применить формулу Ньютона-Лейбница к данному интегралу нельзя. Получим его приближенное значение с помощью рядов. Разделив почленно ряд для  на
на  , имеем
, имеем 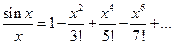 . Отсюда, интегрируя почленно, получаем
. Отсюда, интегрируя почленно, получаем
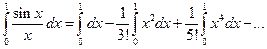
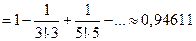 .
.
Ограничившись тремя членами знакочередующегося ряда, получим погрешность 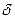 меньше, чем абсолютная величина первого из отброшенных членов
меньше, чем абсолютная величина первого из отброшенных членов 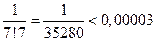 .
.
В том случае, когда функция 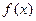 или ее производные не определены в нуле, можно воспользоваться разложением функции в ряд Тейлора
или ее производные не определены в нуле, можно воспользоваться разложением функции в ряд Тейлора
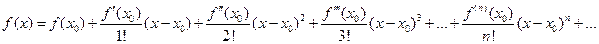 .
.
Ряд Маклорена является его частным случаем при 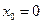 .
.
Задания для самостоятельного решения.
Определить область сходимости следующих рядов.
4.31. 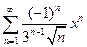 . 4.32.
. 4.32. 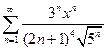 . 4.33.
. 4.33. 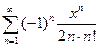 . 4.34.
. 4.34. 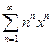 . 4.35.
. 4.35. 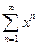
Используя почленное дифференцирование и интегрирование, найти сумму ряда.
4.36. 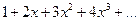 ,
, 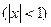 . 4.37.
. 4.37. 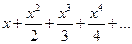 ,
, 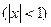 .
.
4.38. 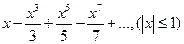 . 4.39.
. 4.39. 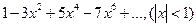 .
.
Разложить в степенной ряд по степеням  функции
функции
4.40. 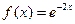 . 4.41.
. 4.41. 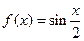 . 4.42.
. 4.42. 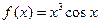 . 4.43.
. 4.43. 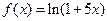 .
.
4.44. 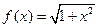 . 4.45.
. 4.45. 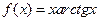 . 4.46.
. 4.46. 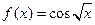 . 4.47.
. 4.47. 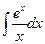 . 4.48.
. 4.48. 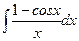 .
.
Вычислить приближенно с точностью до 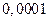 .
.
4.49. 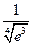 . 4.50.
. 4.50. 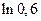 . 4.51.
. 4.51. 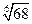 . 4.52.
. 4.52. 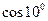 . 4.53.
. 4.53.  .
.
Ответы.
4.31. 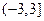 . 4.32.
. 4.32.  . 4.33.
. 4.33.  . 4.34. 0. 4.35.
. 4.34. 0. 4.35. 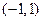 .
.
4.36. 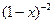 . 4.37.
. 4.37. 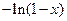 . 4.38.
. 4.38. 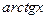 . 4.39.
. 4.39.  . 4.40.
. 4.40. 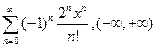 .
.
4.41. 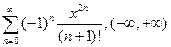 . 4.42.
. 4.42. 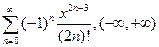 . 4.43.
. 4.43. 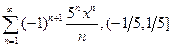 .
.
4.44. 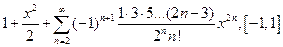 . 4.45.
. 4.45. 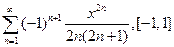 .
.
4.46. 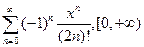 . 4.47.
. 4.47. 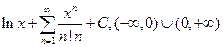 .
.
4.48. 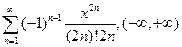 . 4.49.
. 4.49. 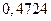 . 4.50.
. 4.50. 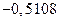 . 4.51.
. 4.51. 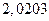 . 4.52.
. 4.52. 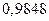 .
.
4.53. 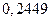 .
.
Контрольная работа № 4. Ряды.
1. - 3. Исследовать ряды на сходимость.
4. Исследовать на сходимость и абсолютную сходимость знакочередующийся ряд.
5. Найти область сходимости степенного ряда.
Вариант 1.
1. 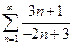 . 2.
. 2. 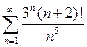 . 3.
. 3. 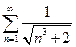 . 4.
. 4.  . 5.
. 5. 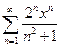 .
.
Вариант 2.
1. 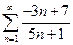 . 2.
. 2. 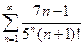 . 3.
. 3. 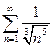 . 4.
. 4. 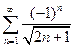 . 5.
. 5. 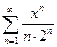 .
.
Вариант 3.
1.  . 2.
. 2. 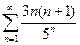 . 3.
. 3. 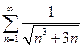 . 4.
. 4. 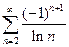 . 5.
. 5. 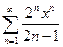 .
.
Вариант 4.
1. 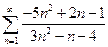 . 2.
. 2. 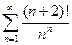 . 3.
. 3. 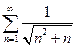 . 4.
. 4. 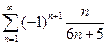 . 5.
. 5. 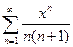 .
.
Вариант 5.
1. 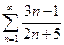 . 2.
. 2. 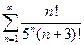 . 3.
. 3. 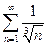 . 4.
. 4. 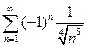 . 5.
. 5. 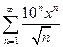 .
.
Вариант 6.
1. 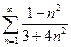 . 2.
. 2. 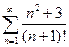 . 3.
. 3. 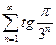 . 4.
. 4. 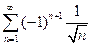 . 5.
. 5. 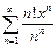 .
.
Вариант 7.
1. 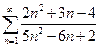 . 2.
. 2. 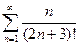 . 3.
. 3. 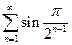 . 4.
. 4. 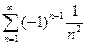 . 5.
. 5. 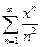 .
.
Вариант 8.
1. 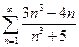 . 2.
. 2. 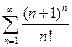 . 3.
. 3.  . 4.
. 4. 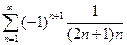 . 5.
. 5. 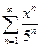 .
.
Вариант 9.
1. 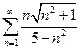 . 2.
. 2. 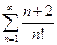 . 3.
. 3. 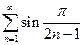 . 4.
. 4. 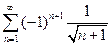 . 5.
. 5. 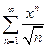 .
.
Вариант 10.
1. 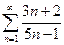 . 2.
. 2. 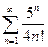 . 3.
. 3. 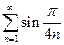 . 4.
. 4. 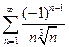 . 5.
. 5. 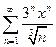 .
.
Вариант 11.
1. 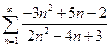 . 2.
. 2. 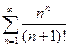 . 3.
. 3. 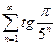 . 4.
. 4. 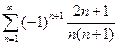 . 5.
. 5. 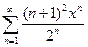 .
.
Вариант 12.
1. 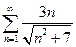 . 2.
. 2. 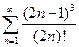 . 3.
. 3. 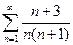 . 4.
. 4. 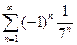 . 5.
. 5. 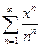 .
.
Вариант 13.
1. 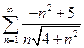 . 2.
. 2.  . 3.
. 3. 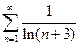 . 4.
. 4. 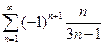 . 5.
. 5. 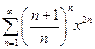 .
.
Вариант 14.
1. 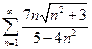 . 2.
. 2.  . 3.
. 3. 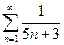 . 4.
. 4. 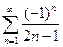 . 5.
. 5. 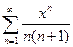 .
.
Вариант 15.
1. 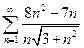 . 2.
. 2. 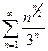 . 3.
. 3. 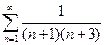 . 4.
. 4. 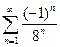 . 5.
. 5. 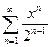 .
.
Вариант 16.
1. 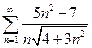 . 2.
. 2. 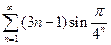 . 3.
. 3. 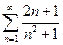 . 4.
. 4. 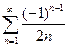 . 5.
. 5. 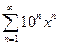 .
.
Вариант 17.
1.  . 2.
. 2. 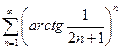 . 3.
. 3. 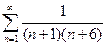 . 4.
. 4. 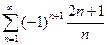 . 5.
. 5. 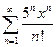 .
.
Вариант 18.
1. 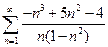 . 2.
. 2. 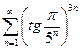 . 3.
. 3. 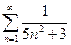 . 4.
. 4.  . 5.
. 5. 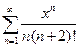 .
.
Вариант 19.
1. 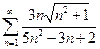 . 2.
. 2. 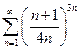 . 3.
. 3. 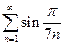 . 4.
. 4. 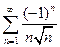 . 5.
. 5. 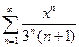 .
.
Вариант 20.
1. 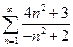 . 2.
. 2. 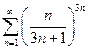 . 3.
. 3. 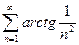 . 4.
. 4. 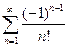 . 5.
. 5. 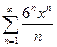 .
.
Вариант 21.
1. 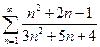 . 2.
. 2. 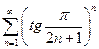 . 3.
. 3. 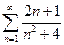 . 4.
. 4. 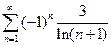 . 5.
. 5.  .
.
Вариант 22.
1. 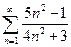 . 2.
. 2. 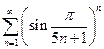 . 3.
. 3. 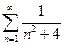 . 4.
. 4. 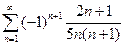 . 5.
. 5.  .
.
Вариант 23.
1. 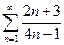 . 2.
. 2. 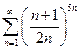 . 3.
. 3. 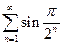 . 4.
. 4. 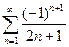 . 5.
. 5. 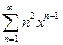 .
.
Вариант 24.
1.  . 2.
. 2. 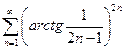 . 3.
. 3. 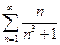 . 4.
. 4. 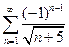 . 5.
. 5. 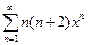 .
.
Вариант 26.
1. 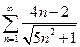 . 2.
. 2. 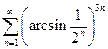 . 3.
. 3. 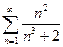 . 4.
. 4. 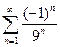 . 5.
. 5. 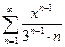 .
.
Вариант 27.
1. 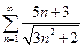 . 2.
. 2. 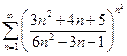 . 3.
. 3. 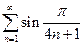 . 4.
. 4. 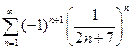 . 5.
. 5. 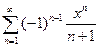 .
.
Вариант 28.
1. 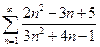 . 2.
. 2. 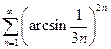 . 3.
. 3. 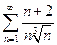 . 4.
. 4. 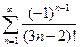 . 5.
. 5. 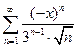 .
.
Вариант 29.
1. 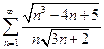 . 2.
. 2. 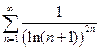 . 3.
. 3. 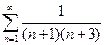 . 4.
. 4. 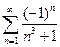 . 5.
. 5. 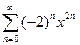 .
.
Вариант 30.
1. 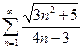 . 2.
. 2. 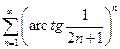 . 3.
. 3. 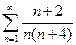 . 4.
. 4. 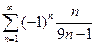 . 5.
. 5. 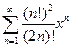 .
.
Вопросы к экзамену по курсу “Математика, 2-ой семестр”.
1. Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла.
Таблица простейших неопределенных интегралов.
2.Разложение подынтегральной функции на слагаемые.Введение функции под знак дифференциала. Метод подстановки.
3. Интегрирование по частям.
4. Интегрирование рациональных выражений.
5. Интегрирование простейших иррациональностей.
6. Интегрирование тригонометрических функций.
7. Интегральная сумма. Определенный интеграл. Геометрический смысл определенного интеграла. Свойства определенногоинтеграла.
8. Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.
9. Замена переменной и интегрирование по частям в определенном интеграле.
10. Вычисление площади плоских фигур.
11. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл).
12. Функция нескольких переменных, область ее определения, множество ее значений.
Функция двух переменных, график, линии уровня. Предел функции двух переменных,
непрерывность, разрыв. Примеры.
13. Частные приращения функции, ее полное приращение. Частные производные первого и
второго порядков. Полный дифференциал.
14. Производная по направлению. Градиент.
15. Экстремум функции двух переменных. Теорема (необходимый признак существования
экстремума). Теорема (достаточные условия экстремума).
16. Дифференциальное уравнение. Общее и частное решения, интегральная кривая. Три
формы записи дифференциального уравнения первого порядка. Задача Коши. Теорема
существования и единственности решения задачи Коши.
17. Уравнение с разделяющимися переменными. Задача о времени полураспада
радиоактивного вещества.
18. Однородная функция. Однородное дифференциальное уравнение.
19. Линейное дифференциальное уравнение первого порядка. Метод вариации произвольной
постоянной. Метод подстановки. Уравнение Бернулли.
20. Дифференциальное уравнение в полных дифференциалах. Признак.
21. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
22. Линейное неоднородное уравнение второго порядка. Структура его общего решения.
Линейное однородное уравнение второго порядка с постоянными коэффициентами.
Характеристическое уравнение. Фундаментальная система решений. Общее решение.
23. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами и
специальной правой частью.
24. Числовой ряд, его частичная сумма. Сходимость и расходимость ряда. Сумма ряда.
Сумма бесконечно убывающей геометрической прогрессии. Свойства числовых рядов.
25. Необходимый признак сходимости и достаточный признак расходимости ряда.
Достаточный признак расходимости. Примеры.
26. Достаточные признаки сходимости знакоположительных рядов. Первый и второй признаки
сравнения. Признак Даламбера. Радикальный признак. Интегральный признак Коши.
Примеры.
27. Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды.
Признак Лейбница. Примеры.
28. Функциональный ряд. Область сходимости. Степенные ряды. Теорема Абеля. Следствие.
Интервал сходимости. Радиус сходимости степенного ряда. Примеры.
29. Разложение функции в степенной ряд. Почленное дифференцирование иинтегрирование
cтепенных рядов. Разложение функций 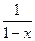 ,
, 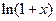 ,
, 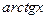 в степенные ряды.
в степенные ряды.
30. Ряды Маклорена и Тейлора. Разложение в ряд Маклорена функций 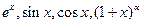
Литература .
1. Дмитрий Письменный. Конспект лекций по высшей математике. 1, 2 части.
Москва. Айрис Пресс. 2005.
2. К.Н. Лунгу, Д.Т. Письменный и др.. Сборник задач по высшей математике. 1,2 курсы.
Москва. Айрис Пресс. 2006.
3. А.А. Гусак. Математический анализ и дифференциальные уравнения. Справочное
пособие к решению задач. Минск. ТетраСистемс. 2006.
4. Б. П. Демидович, В.А. Кудрявцев. Краткий курс высшей математики. Учебное пособие для вузов. Москва. Астрель АСТ. 2004.
5. Ю.И. Клименко. Высшая математика для экономистов в примерах и задачах.
Москва. Экзамен. 2006.
6. Практикум по высшей математике для экономистов. Под редакцией Н.Ш. Кремера.
Москва. Юнити. 2005.
7. О.А. Кострица. Высшая математика для экономистов. Минск. Новое знание. 2006.
8. А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. Математика в экономике. Часть 2. Москва. Финансы и статистика. 2007.
9. М.С. Красс. Математика для экономических специальностей.
Москва. Дело. 2003.
10. С.С. Белявский, Н.А. Широкова. Высшая математика. Решение задач.
Минск. Вышэйшая школа. 2004.
11. М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Сборник задач по обыкновенным дифференциальным уравнениям. Москва. Высшая школа. 1978.
