Матричная модель в обобщенных координатах
Эта модель строится путем добавления еще одного столбца связности.
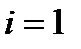, то текущая точка связана с предыдущей;
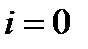, то не связана;
проверяется с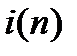 
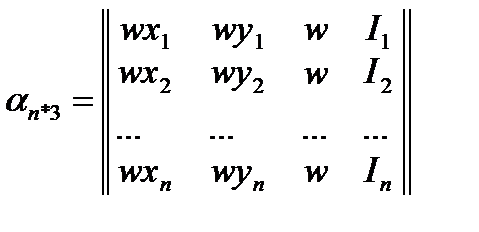
Преимущества:Одинаковое представление объектов;Мощная математика для оперирования над матрицами;Удобство представления операций над матрицами( 
; 
).
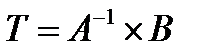Модели преобразования ГО и их классификация.
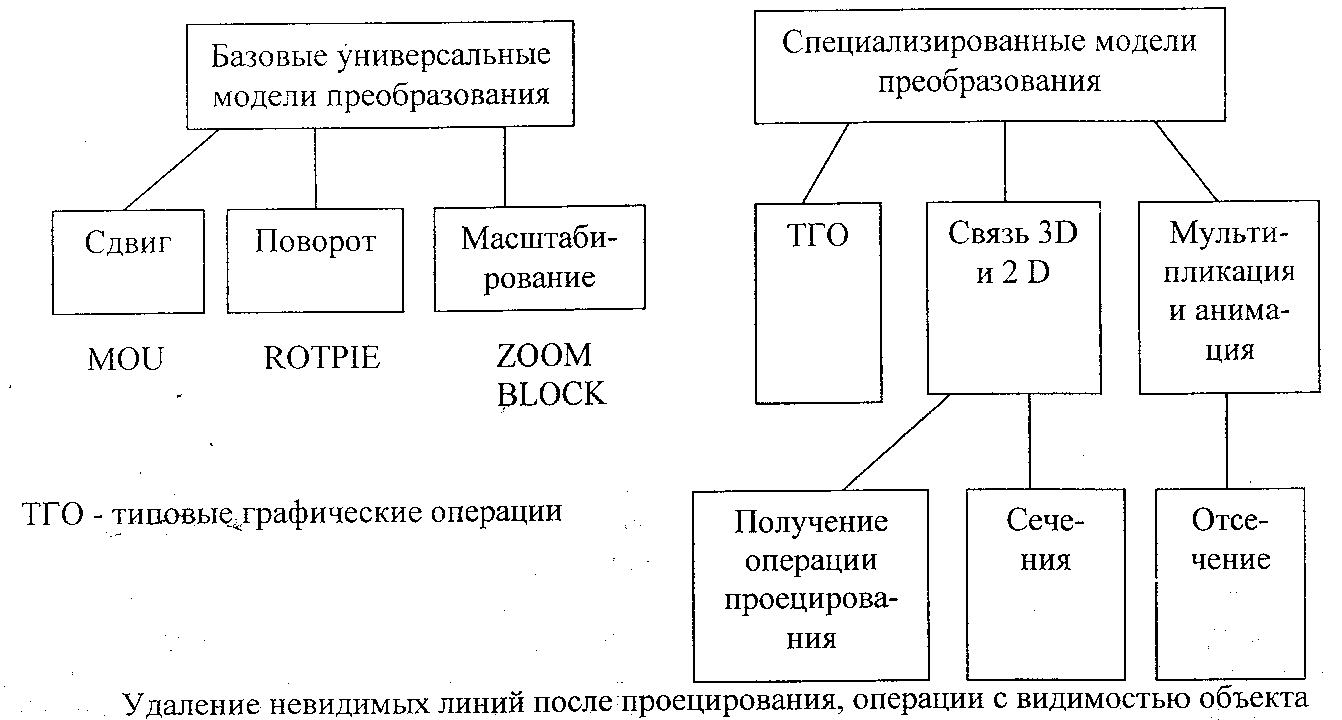
К специальным операциям также относят нелинейные преобразования: композиция; декомпозиция.
Связь 3D и 2D – проецирование, сечение, удаление невидимых линий.
Линейные преобразования ГО (масштабирование, поворот, сдвиг).
Сдвиг (move):
в 2D: x’=x+∆x; y’=y+∆y в 3D:
|1 0 0 0|
|0 1 0 0| - матрица сдвига
|0 0 1 0|
res=
|wx1 wy1 w|
|wx2 wy2 w|
…
|wxn wyn w|
однородные координаты
|1 0 0 |* |0 1 0 | =|∆x ∆y 1|
|wx1’ wy1’ w|
…
|wxn’ wyn’ w|