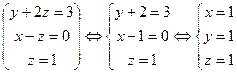Сызықтық теңдеулер жүйесін Крамер ережесімен шешу

1. Жүйені Крамер әдісімен шығар. Келесідей белгілеулер енгізейік:

∆ анықтауышы (1) жүйенің анықтауышы деп аталады. ∆_х, ∆_у, ∆_z анықтауыштары ∆ жүйенің анықтауышынан сәйкес бірінші, екінші, үшінші бағандарын бос мүше элементтерімен ауыстыру арқылы алынған. Екі жағдай қарастырайық.

1 жағдай. 0.Бұл жағдайда(1)жүйенің шешуі бар жәнеол біреу ғана, және келесі формуламен анықталады:

X=∆_x / ∆ y= ∆_y /∆ z=∆_z / ∆

(2) формулалары Крамера формулалары деп аталады.

2 жағдай. ∆=0, ∆_х=∆_у= ∆_z=0

Бұл жағдайда (1) жүйенің шексіз көп шешімі болады (шешуі

болмауы да мүмкін).
Біртекті жүйені қарастырайық.
Мұндағы h1 = h2 = h3	=0, яғни:
a1x+ b1y+ c1z= 0
a2x+ b2 y +c2 z= 0
a3x+ b3 y+ c3z= 0

Егер 0 болса,онда (3) жүйенің бір ғана нольдік шешімі х=0, у=0, z=0 болады.

1) Айталық ∆ анықтауыштың бір миноры нольден өзгеше

болсын. Айталық, мәселен	a1	b1	≠0. Онда
		a2	b2
a1x+ b1y+ c1z= 0	a1x +b1y=- c1z
→
a2 x+b2 y+ c2 z= 0	a2 x+ b2 y=- c2 z

Үш белгісізді екі теңдеуден тұратын біртекті жүйе аламыз.

∆ 1=

a1

b1

≠0

∆ 2

=

-с1z b1

=z

b1 с1

;

a1

c1 z

z

a1 с1

a2

b2

-c 2 z b 2

b 2 c2

a2

c 2 z

a2 с2

Онда (4) жүйенің шешімі Крамер формулалары бойынша

b1 c1

z

a1 c1

z

2

b2 c2

3

a

2 c2

a1 b1

x

; y

;z t

t

a

b

a

b

a

b

a2

b2

a2

b2

деп алайық; мұндағы t кез келген мән қабылдайды. Онда (4) біртекті жүйенің келесі формулалармен анықталған шексіз көп шешімі болады:

x	b1	c1	t, y	a1	b1	t; z	a1	b1	t	(5)
	b2	c2		a2	b2		a2	b2

2) Айталық анықтауыштың барлық минорлары нольге тең болсын. Бұл дегеніміз (3) барлық үш теңдеудің коэффициенттерінің пропорционалдығын білдіреді. Онда бір ғана

теңдеу

a1x +b1 y+ c1z= 0

шығады және

оның шексіз көп

шешімі болады.

∆ =0 ,бірақ анықтауыштың біреуінің мәні нольден өзгеше.

Онда

формуладан

алатынымыз,

∆*x=∆x ;∆* y= ∆ y ;∆*z= ∆ z .Егер∆ x

≠0деп есептесек,

онда теңдікте

∆*x= 0; ∆ x

≠0 мүмкін

емес жағдай аламыз.

Яғни (1) жүйенің шешімі жоқ.

18.п- белгісізі бар м сызықты теңдеулер жүйесі,Гаусc теориясы.

А және А векторы матрицаларының ранглерін Гаус әдісімен анықтау үшін А векторы кеңейтілген матрицасын элементар түрлендірулер арқылы трапеция тәріздер матрицаға келтіреді

1.r(Aвекторы)>r(A).Бұл жағдайда Кронекер-Капелли теоремасы теңдеулер жүйесі үйлесімсіз.

2.r(Aвекторы)=r(A)=r.Бұл жағдайда сол теорема бойынша жүйе үйлесімді.Сонымен бірге:

а . Егер r=n болса,яғни матрицаның ранглері белгісіздер санына тең болса онда жүйе шешімі жалғыз болады.

б . Егер r<n болса,онда теңдеулер жүйесінің параметрлері тәуелді ақырсыз көп шешімі болады.

Мысалы. Теңдеулер жүйесін зерттеп үйлесімді болған жағдайда оның шешімін табу керке.

~ ~ ~

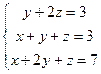
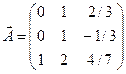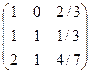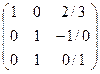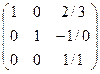
Мұндағы r(Aвекторы)=r(A)=3.Бұл 2а.жағдайы.Теңдеулер жүйесінің жалғыз шешімі бар соңғы матрицадан теңдеулер жүйесі қалыпты түрде жазып,оның шешімін табамыз.