Теоремы сложения и умножения
Основные теоремы теории вероятностей 1
Алгебра событий
1. Возможны всего 4 исхода. Перечислите все события. Каково их число?
2. Каков смысл равенств 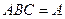 ,
, 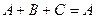 ?
?
3. Упростите 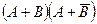 .
.
4. Имеются три одинаковые урны, в каждой из которых лежат неразличимые на ощупь белые и черные шары. Опыт состоит в выборе произвольной урны и вынимании произвольного шара. Пусть
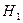 − выбрали первую урну.
− выбрали первую урну.
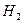 − выбрали вторую урну.
− выбрали вторую урну.
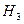 − выбрали третью урну.
− выбрали третью урну.
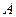 − вынули из урны белый шар.
− вынули из урны белый шар.
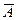 − вынули из урны черный шар.
− вынули из урны черный шар.
1) Запишите с помощью символов следующие события.
а) Выбрали либо первую, либо вторую урну.
б) Выбрали какую-то одну урну.
в) Выбрали не первую урну.
г) Белый шар вынули из первой урны.
д) Черный шар вынули из третьей урны.
е) Белый шар вынули не из второй урны.
ж) Из какой-то урны выбрали черный шар.
2) Дайте словесное толкование следующим событиям.
а) 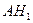 . б)
. б) 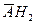 . в)
. в) 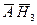 . г)
. г) 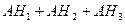 . д)
. д) 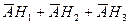 .
.
3) Установите, верны ли равенства:
а) 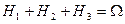 , б)
, б) 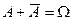 , в)
, в) 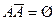 и дайте им словесное толкование.
и дайте им словесное толкование.
4) Известно, что в каждой из урн число белых шаров равно числу черных (например, по одному). Подсчитайте указанные вероятности.
а) 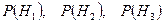 , б)
, б) 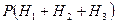 , в)
, в) 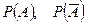 , г)
, г) 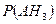 ,
, 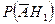 .
.
5) Запишите словами, в чем состоят указанные ниже события, и вычислите их вероятность.
а) 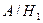 , б)
, б) 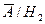 , в)
, в) 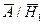 .
.
Теоремы сложения и умножения
1. Каждое из четырех несовместных событий может произойти с вероятностями 0,012, 0,010, 0,006 и 0,002 соответственно. Определите вероятность того, что в результате опыта произойдет хотя бы одно из этих событий.
2. Каждое из четырех независимыхсобытий может произойти с вероятностями 0,012, 0,010, 0,006 и 0,002 соответственно. Определите вероятность того, что в результате опыта произойдет хотя бы одно из этих событий.
3. При увеличении напряжения может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов, вероятности отказа которых равны 0,2, 0,3 и 0,4 соответственно. Определите вероятность того, что разрыва цепи не будет.
4. Пользователь компьютера давно не обновлял антивирусные базы. Поэтому новый вирус может быть обнаружен с вероятностью 0,6. Если вирус не обнаружен, то он поражает наиболее ценные файлы с вероятностью 0,8. Какова вероятность поражения ценных файлов?
5. Вероятность брака из-за нарушения режима обработки деталей равна 0,02, а вследствие неисправности станка 0,08. Какова вероятность выпуска бракованных деталей?
6. Два станка работают независимо друг от друга. Вероятность бесперебойной работы первого в течение смены 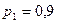 , второго
, второго 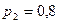 . Какова вероятность
. Какова вероятность
а) бесперебойной работы обоих станков в течение смены,
б) выхода из строя обоих станков,
в) бесперебойной работы хотя бы одного из этих станков?
7. Три стрелка делают по одному выстрелу по мишени. Вероятность попадания первого 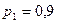 , второго
, второго 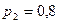 , третьего
, третьего 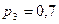 . Найдите вероятность того, что
. Найдите вероятность того, что
а) все стрелки попадут в мишень,
б) только один попадет в мишень,
в) все промахнутся,
г) хотя бы один попадет в мишень?
8. Экзаменационный билет содержит три вопроса. Вероятности того, что студент ответит на первый и второй вопросы равны по 0,9, а на третий − 0,8. Найдите вероятность того, что студент сдаст экзамен, если для этого необходимо ответить
а) на все вопросы,
б) хотя бы на два вопроса.
9. Имеется коробка с 9 новыми теннисными мячами. Для игры берут 3 мяча; после игры их кладут обратно. При выборе мячей игранные от неигранных не отличают. Какова вероятность того, что после трех игр в коробке не останется неигранных мячей?
10. В зрительном зале кинотеатра имеется 9 рядов, пронумерованных подряд от 1 до 9, а в каждом ряду по 9 мест, также пронумерованных от 1 до 9. Зритель наудачу занимает место. Что вероятнее: сумма номеров ряда и места в ряду окажется четной или нечетной?
11. Имеются три электрические схемы, состоящие каждая из 4 выключателей, каждый из которых с вероятностью 0,5 может быть включен и выключен. Выяснить, для какой из схем вероятность того, что ток будет проходить от точки А к точке В, будет наибольшей (схема 1).
Та же задача при условии, что первый выключатель включен с вероятностью 0,6, второй − с вероятностью 0,7, третий − с вероятностью 0,8, четвертый − с вероятностью 0,9.
12. Частица поглощается стенкой с вероятностью 0,5. Какое минимальное число таких стенок надо поставить на пути частицы, чтобы они поглотили эту частицу с вероятностью, не меньшей, чем 0,999?
13. В одном маленьком французском городке полиция разыскивает бродягу. Можно считать, что есть 4 шанса из 5, что он находится в одном из 8 баров городка, безразлично в каком − он не отдает предпочтения ни одному из них. Полицейские посетили 7 баров, но бродягу не обнаружили. Каковы шансы найти его в восьмом баре?
14. Дворцовый чеканщик кладет в каждый ящик вместимостью в 100 монет одну фальшивую. Король подозревает чеканщика и подвергает проверке монеты, взятые наудачу по одной в каждом из 100 ящиков. Какова вероятность, что чеканщик не будет разоблачен?
Дополнительные задачи
1. Каждую секунду с вероятностью 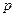 независимо от других моментов времени по дороге проезжает машина. Для перехода дороги пешеходу необходимо 3 с. Какова вероятность того, что подошедший к дороге пешеход будет ожидать возможности перехода а) 3 с, б) 4 с, в) 5 с?
независимо от других моментов времени по дороге проезжает машина. Для перехода дороги пешеходу необходимо 3 с. Какова вероятность того, что подошедший к дороге пешеход будет ожидать возможности перехода а) 3 с, б) 4 с, в) 5 с?
2. На большой улице с односторонним движением расположены один за другим два светофора; каждый из светофоров устроен так, что промежуток времени, когда в нем горит зеленый свет, составляет две трети всего времени работы светофора. Автомобилист заметил, что когда он, двигаясь с обычной скоростью, проезжает на зеленый свет первый светофор, то в 3 случаях из 4 и второй светофор его не задерживает. Допустим теперь, что автомобилист проскочил первый светофор при красном свете. Чему равна вероятность того, что и на втором светофоре будет гореть красный свет?
