Миноры и алгебраические дополнения
Минором 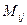 элемента
элемента 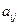 определителя (матрицы)
определителя (матрицы) 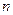 -го порядка называется определитель матрицы
-го порядка называется определитель матрицы 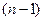 - го порядка, полученной из матрицы
- го порядка, полученной из матрицы 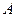 вычеркиванием
вычеркиванием 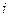 - строки и
- строки и 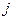 - го столбца.
- го столбца.
Например, минором элемента 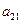 матрицы
матрицы 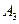 третьего порядка будет определитель второго порядка, полученный вычеркиванием 2-ой строки и 1-го столбца:
третьего порядка будет определитель второго порядка, полученный вычеркиванием 2-ой строки и 1-го столбца:


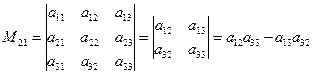 .
.
Каждая матрица 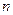 -го порядка имеет
-го порядка имеет 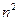 миноров
миноров 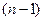 порядка.
порядка.
Алгебраическим дополнением 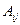 элемента
элемента 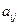 определителя (матрицы)
определителя (матрицы) 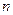 - го порядка называется его минор, взятый со знаком
- го порядка называется его минор, взятый со знаком 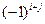 :
:
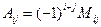 (2.5)
(2.5)
Например, 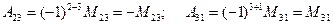 .
.
Теорема Лапласа[2]. Определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения[3]:
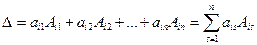 (2.6)
(2.6)
(разложение по элементам 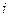 -ой строки;
-ой строки; 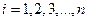 )
)
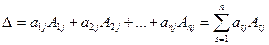 (2.7)
(2.7)
(разложение по элементам 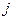 - го столбца;
- го столбца; 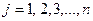 )
)
Пример 4.Вычислить определитель 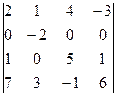 .
.
Решение: Вычислим определитель разложением по элементам второй строки, т.к. в ней содержится максимальное количество нулевых элементов:
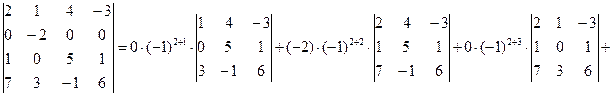
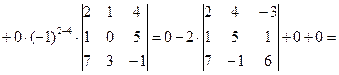 [разложим последний определитель по элементам первой строки]=
[разложим последний определитель по элементам первой строки]= 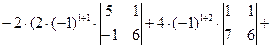
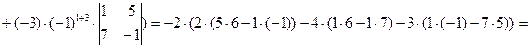
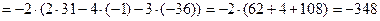 .
.
Определитель треугольного (и, очевидно, диагонального) вида равен произведению элементов главной диагонали.
Пример 5.Вычислить определитель 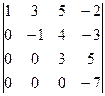 .
.
Решение: 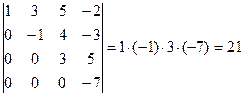 .
.
Свойства определителей
10. Если определитель содержит нулевую строку (или столбец), то он равен нулю.
20. Если все элементы какой-либо строки (столбца) определителя умножить на число 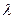 , то определитель умножится на это число.
, то определитель умножится на это число.
Замечание: За знак определителя можно выносить общий множитель всех его элементов.
30. При транспонировании определитель не изменяется, т.е. 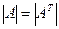 .
.
40. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
50. Если определитель содержит две одинаковые строки (столбца), то он равен нулю.
60. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.
70. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю, т.е. 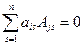 при
при 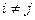 .
.
80. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), умноженные на одно и то же число.
90. Сумма произведений привольных чисел 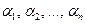 на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной матрицы заменой элементов этой строки (столбца) на числа
на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной матрицы заменой элементов этой строки (столбца) на числа 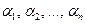 .
.
100. Определитель произведения двух квадратных матриц равен произведению их определителей: 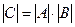 , если
, если 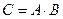 ,
, 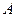 и
и 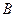 - матрицы
- матрицы 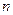 - го порядка.
- го порядка.
Замечание: Если 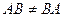 , то
, то 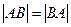 .
.
Перечисленные свойства определителей позволяют значительно упростить их вычисления, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать его с помощью свойств 10-90, чтобы преобразованный определитель имел строку (или столбец), содержащую как можно больше нулей, а затем найти определитель разложением по этой строке (столбцу).
Пример 6.Вычислить определитель четвертого порядка 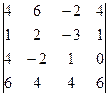 .
.
Решение: Преобразуем определитель так, чтобы, в третьей строке все элементы кроме одного обрались в нуль. Для этого умножим, например, элементы третьего столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-ого и 2-ого столбцов. Получим
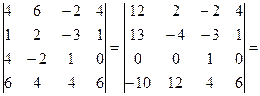 [разложим полученный определитель по элементам третьей строки]=
[разложим полученный определитель по элементам третьей строки]= 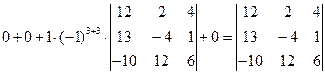 .
.
Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, но можно продолжить «упрощение» матрицы. Например, «обнулим» элементы второй строки (кроме одного):
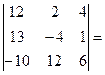 [прибавим к элементам первого столбца матрицы соответствующие элементы третьего столбца, умноженные на (-13)]=
[прибавим к элементам первого столбца матрицы соответствующие элементы третьего столбца, умноженные на (-13)]= 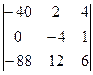 =[к элементам второго столбца прибавим соответственные элементы третьего столбца, умноженные на 4]=
=[к элементам второго столбца прибавим соответственные элементы третьего столбца, умноженные на 4]= 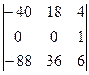 . Раскладывая по элементам второй строки и вынося общие множители элементов первой строки и второй строки за знак определителя, получаем
. Раскладывая по элементам второй строки и вынося общие множители элементов первой строки и второй строки за знак определителя, получаем
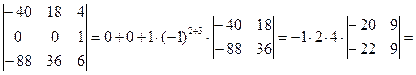 [теперь вынесем за знак определителя общий множитель элементов первого столбца и элементов второго столбца]=
[теперь вынесем за знак определителя общий множитель элементов первого столбца и элементов второго столбца]=
= 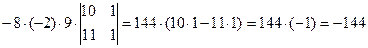 .
.
Ранг матрицы
В матрице 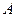 размера
размера 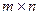 вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы
вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы 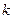 - го порядка, где
- го порядка, где 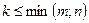 , где
, где 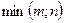 – меньшее из чисел m и n. Определители таких подматриц называются минорами
– меньшее из чисел m и n. Определители таких подматриц называются минорами 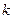 -го порядка матрицы
-го порядка матрицы 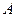 .
.
Например, из матрицы 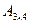 можно получить подматрицы первого, второго и третьего порядков.
можно получить подматрицы первого, второго и третьего порядков.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы 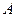 обозначается
обозначается 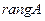 , или
, или 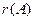 .
.
Минор, который определяет ранг матрицы, называетсябазисным. У матрицы может быть несколько базисных миноров.
Из определения следует:
а) ранг матрицы 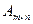 не превосходит меньшего из ее размеров, т.е.
не превосходит меньшего из ее размеров, т.е. 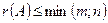 ;
;
б) 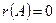 тогда и только тогда, когда все элементы матрицы равны нулю, т.е.
тогда и только тогда, когда все элементы матрицы равны нулю, т.е. 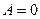 ;
;
в) для квадратной матрицы 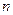 -го порядка
-го порядка 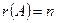 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 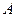 - невырожденная.
- невырожденная.
Пример 7.Найти ранг матрицы 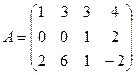 и указать один из базисных миноров.
и указать один из базисных миноров.
Решение: Так как у матрицы 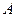 есть ненулевые элементы, то
есть ненулевые элементы, то 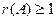 . Найдем какой-нибудь ненулевой минор 2-го порядка (если он существует). Таким минором является, например,
. Найдем какой-нибудь ненулевой минор 2-го порядка (если он существует). Таким минором является, например, 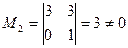 . Значит,
. Значит, 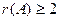 .
.
Вычислим миноры 3-го порядка, окаймляющие 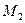 :
:
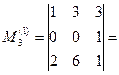 [разложим определитель по второй строке]= =
[разложим определитель по второй строке]= = 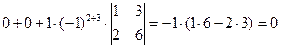 ;
;
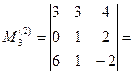 [разложим определитель по 1-ому столбцу]= =
[разложим определитель по 1-ому столбцу]= = 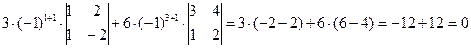 .
.
Все миноры 3-го порядка, окаймляющие 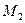 , равны нулю, следовательно,
, равны нулю, следовательно, 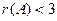 . Итак,
. Итак, 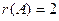 .
.
Одним из базисных миноров является 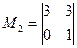 .
.
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы.
К элементарным преобразованиям относятся следующие:
1) отбрасывание нулевой строки (столбца).
2) умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
3) изменение порядка строк (столбцов) матрицы.
4) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5) транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Две матрицы называются эквивалентными, если одна получается из другой с помощью эквивалентных преобразований. Обозначается эквивалентность знаком ~.
Из теоремы следует, что эквивалентные матрицы имеют одинаковые ранги.
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, тогда вычисление ее ранга не представляет труда.
Матрица А называется ступенчатой, если она имеет вид:
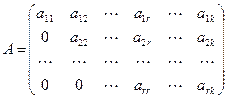 (3.1)
(3.1)
где 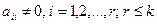 .
.
Замечание. Условие 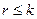 всегда может быть достигнуто транспонированием матрицы.
всегда может быть достигнуто транспонированием матрицы.
Очевидно, что ранг ступенчатой матрицы равен 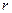 , так как имеется минор
, так как имеется минор 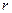 - го порядка, не равный нулю:
- го порядка, не равный нулю:
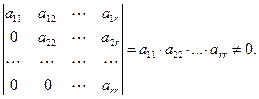
Алгоритм вычисления ранга матрицы с помощью элементарных преобразований покажем на примере.
Пример 8.Найти рангматрицы 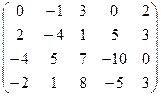 методом элементарных преобразований.
методом элементарных преобразований.
Решение: 1. Если 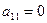 , то перестановкой строк или столбцов добиваемся того, что
, то перестановкой строк или столбцов добиваемся того, что 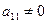 . В данном примере поменяем местами, например, первую и вторую строки.
. В данном примере поменяем местами, например, первую и вторую строки.
2. Если 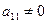 , то умножая элементы первой строки на подходящие числа (а именно, на 0, 2 и 1) и прибавляя полученные числа соответственно к элементам второй[4], третьей и четвертой строк, добьемся, чтобы все элементы первого столбца (кроме
, то умножая элементы первой строки на подходящие числа (а именно, на 0, 2 и 1) и прибавляя полученные числа соответственно к элементам второй[4], третьей и четвертой строк, добьемся, чтобы все элементы первого столбца (кроме 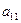 ) равнялись нулю:
) равнялись нулю:
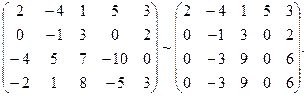
3. Если в полученной матрице 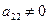 (в нашем примере
(в нашем примере 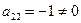 ), то умножая элементы второй строки на подходящие числа (а именно на -3 и -3) и прибавляя полученные числа соответственно к элементам третьей и четвертой строк, добьемся, чтобы все элементы второго столбца (кроме
), то умножая элементы второй строки на подходящие числа (а именно на -3 и -3) и прибавляя полученные числа соответственно к элементам третьей и четвертой строк, добьемся, чтобы все элементы второго столбца (кроме 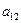 и
и 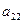 ) равнялись нулю. Если в процессе преобразований получаются нулевые строки (или столбцы) (как в данном примере), то их следует отбросить:
) равнялись нулю. Если в процессе преобразований получаются нулевые строки (или столбцы) (как в данном примере), то их следует отбросить:
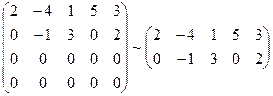 .
.
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например, 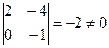 .
.
Поэтому ранг полученной ступенчатой, а следовательно, и данной матрицы равен 2.
Для рангов матриц справедливы следующие соотношения:
1) 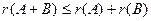 ; 2)
; 2) 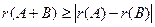 ;
;
3) 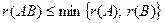 ; 4)
; 4) 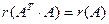 ;
;
5) 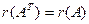 ; 6)
; 6) 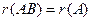 , если
, если 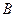 - квадратная матрица и
- квадратная матрица и 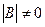 ;
;
7)  , если
, если 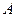 и
и 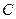 - квадратные матрицы и
- квадратные матрицы и 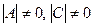 ;
;
8) 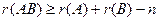 , где
, где 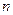 - число столбцов матрицы
- число столбцов матрицы 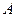 или строк матрицы
или строк матрицы 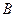 .
.
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк (или столбцов).
Пусть строки матрицы 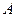
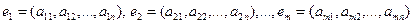 .
.
Строка 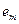 называется линейной комбинацией строк
называется линейной комбинацией строк 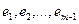 матрицы, если
матрицы, если
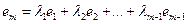 (3.2)
(3.2)
где 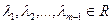 . (Равенство (3.2) понимается в смысле поэлементного сложения строк)
. (Равенство (3.2) понимается в смысле поэлементного сложения строк)
Строки матрицы 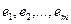 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 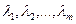 , из которых хотя бы одно отлично от нуля, что линейная комбинация строк равна нулевой строке:
, из которых хотя бы одно отлично от нуля, что линейная комбинация строк равна нулевой строке:
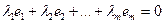 (3.3)
(3.3)
где 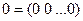 .
.
Если равенство (3.3) выполняется тогда и только тогда, когда 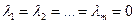 , то строки матрицы называются линейно независимыми.
, то строки матрицы называются линейно независимыми.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк и столбцов, через которые линейно выражаются все ее остальные строки (столбцы).
В предыдущем примере число линейно независимых строк матрицы равно 2.
Обратная матрица
Для каждого числа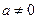 существует обратное число
существует обратное число 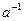 такое, что произведение
такое, что произведение 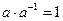 . Для квадратных матриц тоже вводится аналогичное понятие.
. Для квадратных матриц тоже вводится аналогичное понятие.
Матрица 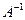 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
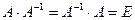 (4.1)
(4.1)
Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную.
Если определитель матрицы отличен от нуля 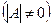 , то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при
, то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при 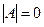 ) — вырожденной, или особенной.
) — вырожденной, или особенной.
Присоединенной матрицей к квадратной матрице 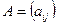 называется матрица
называется матрица 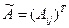 , полученная транспонированием из матрицы, составленной из алгебраических дополнений
, полученная транспонированием из матрицы, составленной из алгебраических дополнений 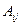 к элементам
к элементам 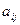 .
.
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 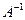 существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная. Причем
существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная. Причем
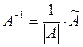 (4.2)
(4.2)
где 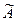 - матрица, присоединенная к матрице
- матрица, присоединенная к матрице 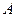 .
.
Алгоритм вычисления обратной матрицы:
10. Находим определитель исходной матрицы. Если 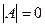 , то матрица
, то матрица 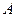 вырожденная и обратной матрицы
вырожденная и обратной матрицы 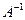 не существует. Если
не существует. Если 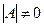 , то матрица
, то матрица 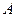 невырожденная и обратная матрица существует.
невырожденная и обратная матрица существует.
20. Находим матрицу 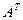 , транспонированную к
, транспонированную к 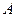 .
.
30. Находим алгебраические дополнения элементов транспонированной матрицы 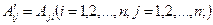 и составляем из них присоединенную матрицу
и составляем из них присоединенную матрицу 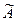 :
: 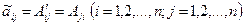 .
.
40. Вычисляем обратную матрицу по формуле.
50. Проверяем правильность вычисления обратной матрицы 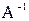 , исходя из ее определения
, исходя из ее определения 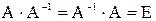 (п. 5° не обязателен).
(п. 5° не обязателен).
Пример 9.Найти матрицу, обратную к матрице 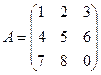 .
.
Решение:
1. Найдем определитель матрицы 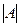 :
: 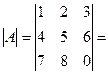 [разложим по элементам 1-ой строки] =
[разложим по элементам 1-ой строки] = 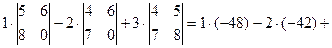
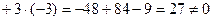 .
.
2. Найдем алгебраические дополнения ко всем элементам матрицы 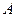 :
:
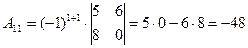 ;
;
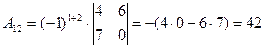 ;
;
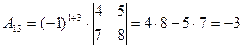 ;
;
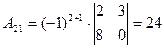 ;
; 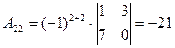 ;
;
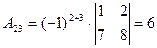 ;
; 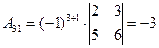 ;
;
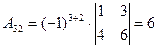 ;
; 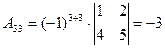 .
.
3. Запишем матрицу 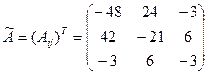 .
.
4. Найдем матрицу 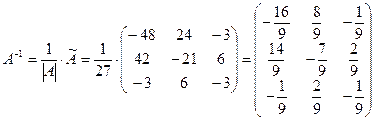 .
.
5. Сделаем проверку:
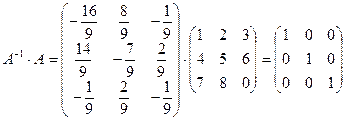 ;
;
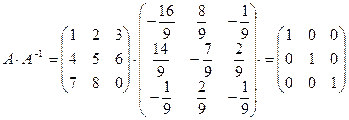 .
.
Для невырожденных матриц выполняются следующие свойства:
10. 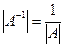 ; 20.
; 20. 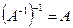 ; 30.
; 30. 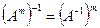 ; 40.
; 40. 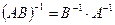 .
.
Можно показать, что любую невырожденную матрицу 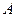 с помощью элементарных преобразований только строк или только столбцов можно привести к единичной матрице
с помощью элементарных преобразований только строк или только столбцов можно привести к единичной матрице 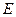 того же порядка. При этом те же преобразования, совершенный над матрицей
того же порядка. При этом те же преобразования, совершенный над матрицей 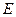 в том же порядке, приводят ее к обратной матрице
в том же порядке, приводят ее к обратной матрице 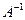 . На этом основан еще один способ нахождения обратной матрицы. Удобно совершать элементарные преобразования над матрицами
. На этом основан еще один способ нахождения обратной матрицы. Удобно совершать элементарные преобразования над матрицами 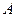 и
и 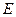 одновременно, записывая их рядом через черту.
одновременно, записывая их рядом через черту.
Пример 10.Найти с помощью элементарных преобразований матрицу, обратную к матрице 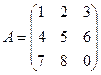 .
.
Решение: 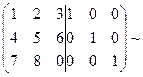 [умножим элементы первой строки на (-4) и (-7) и прибавим соответственно к элементам 2-ой и 3-ей строк]
[умножим элементы первой строки на (-4) и (-7) и прибавим соответственно к элементам 2-ой и 3-ей строк] 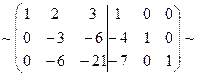 [к третьей строке прибавим вторую, умноженную на (-2). Затем, элементы второй строки разделим на(-3)]
[к третьей строке прибавим вторую, умноженную на (-2). Затем, элементы второй строки разделим на(-3)] 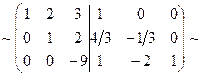 [третью строку разделим на(-9). Затем ко второй строке прибавим третью, умноженную на (-2)]
[третью строку разделим на(-9). Затем ко второй строке прибавим третью, умноженную на (-2)] 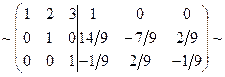 [к элементам первой строки прибавим соответственные элементы третьей строки, умноженные на (-3) и второй, умноженной на (-2)]
[к элементам первой строки прибавим соответственные элементы третьей строки, умноженные на (-3) и второй, умноженной на (-2)] 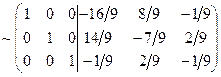 .
.
Полученная (справа от вертикальной черты) матрица совпадает с найденной в примере 9.
[1] Саррус Пьер Фредерик (1798-1861) - математик
[2] Лаплас Пьер Симон (1749 – 1827) – французский астроном, математик и физик.
[3] Точнее, данная теорема является частным случаем теоремы Лапласа.
[4] Вторая строка не меняется, т.к. в данном примере
