Лекція1: Наближене розв`язування нелінійних рівнянь
1.Постановка задачі
2.Виділення кореня рівняння
· Умови виділення кореня
· Графічний метод
· Метод проб
· Метод виділення проміжків монотонності
3.Оцінка наближеного значення кореня
1.Постановка задачі.Задача розв`язання рівняння часто всього зустрічається при вивченні загально-технічних і спеціальних дисциплін, в інженерній практиці. Знайти точне значення кореня рівняння можливе лише в деяких окремих часткових випадках, причому навіть в цих випадках формули знаходження коренів бувають настільки громіздкими ( наприклад, формули коренів алгебраїчних рівнянь третього і четвертого степенів), що ними важко користуватися. Крім того, часто константи, що входять у рівняння, відомі наближено, а також точне значення кореня, як, наприклад, х= 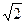 , все рівно приходиться замінити його наближеним значенням. Тому при розв`язуванні рівнянь широко використовуються методи, які дозволяють одержати наближений розв`язок з будь-якою заданою точністю.
, все рівно приходиться замінити його наближеним значенням. Тому при розв`язуванні рівнянь широко використовуються методи, які дозволяють одержати наближений розв`язок з будь-якою заданою точністю.
Нехай задано рівняння f(x)=0, де функція f(x) визначена і неперервна на деякому відрізку і має на ньому неперервні першу і другу похідні. Корені заданого рівняння являються нулями функції y=f(x) і геометрично представляють собою точки перетину її графіку з віссю Ох.
Розглянемо задачу відшукання наближених значень дійсних коренів заданого рівняння з будь-якою заданою точністю. Розв`язок задачі складається з двох етапів:
1. 1. Виділення ( ізоляція) кореня, тобто відшукання відрізка [a;b], який належить області визначення функції y=f(x), на якому знаходиться один і тільки один корінь рівняння f(x)=0.
2. 2. Обчислення або уточнення значення кореня з наперед заданою точністю.
Виділення кореня засновується на двох очевидних фактах.
1) 1) На кінцях відрізка [a;b] функція має різні знаки, тобто f(a)*f(b)<0. Очевидно, що при цьому всередині відрізка [a;b] є принаймні один корінь рівняння f(x)=0. Геометрично це означає, що графік функції y=f(x) в точках a і b
знаходиться по різних сторонах від осі ох і, відповідно, всередині відрізка [a;b] обов`язково повинен перетинати вісь ох. Однак ця умова не гарантує існування єдиного кореня. Так, наприклад, на рис.1 f(a)<0, f(b)>0 і всередині відрізка [a;b] є два різних кореня.
Замітимо, що якщо на кінцях відрізка значення функції має один і той самий знак, то це зовсім не означає, що корінь відсутній. Наприклад, відрізок [a1;b1] (див. рис.1) містить корінь х  (точка х
(точка х  , показана на рис.1, являється кратним коренем рівняння f(x)=0. Далі такі корені розглядати не будемо), але f(a1)>0 і f(b1)>0.
, показана на рис.1, являється кратним коренем рівняння f(x)=0. Далі такі корені розглядати не будемо), але f(a1)>0 і f(b1)>0.
Для існування єдиного кореня на [a;b] повинен мати місце ще один факт.
2) 2) На відрізку [a;b] функція f(x) монотонна, тобто її похідна не міняє знак на [a;b].
Умови 1) і 2) являються достатніми для існування єдиного кореня рівняння f(x)=0. На рис.1 видно, що умови 1) і 2) задовольняють відрізок [a;a  ], а на відрізку [a;b] функція не монотонна.
], а на відрізку [a;b] функція не монотонна.
Задача визначення кореня рівняння f(x)=0 являється у відшуканні відрізка [a;b] області визначення функції y=f(x), на якому виконуються три умови:
1) 1) f(a)*f(b)<0;
2) 2) f  (x) не міняє знак для х
(x) не міняє знак для х 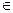 [a;b];
[a;b];
3) 3) f  (x) не міняє знак для х
(x) не міняє знак для х 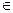 [a;b].
[a;b].
Третя умова означає, що графік функції або тільки випуклий, або тільки вгнутий на відрізку [a;b].
На рис.2 визначені всі можливі варіанти розміщення графіка функції на відрізку [a;b] при виконанні умов 1)-3).
Відрізок [a;b] при виконанні умов 1)-3) для функції f(x) називають відрізком, що виділяє корінь даної функції.
Виділення кореня можна проводити як аналітично, так і графічно.
Графічні корені рівняння  f(x)=0 можна виділити, побудувавши графік функції y=f(x) і наближено визначивши точки його перетину з віссю ох. Однак задача побудови графіку не завжди проста. Звично рівняння f(x)=0 заміняють еквівалентним рівнянням
f(x)=0 можна виділити, побудувавши графік функції y=f(x) і наближено визначивши точки його перетину з віссю ох. Однак задача побудови графіку не завжди проста. Звично рівняння f(x)=0 заміняють еквівалентним рівнянням 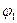 (х)=
(х)= 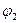 (х) ( f(x)=
(х) ( f(x)= 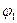 (х)-
(х)- 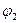 (х)), підбирають функції y
(х)), підбирають функції y  =
= 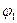 (х) і у
(х) і у  =
= 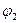 (х) так, щоб будувати їх графіки було простіше, чим графік функції y=f(x). Абсциси точок перетину графіків y
(х) так, щоб будувати їх графіки було простіше, чим графік функції y=f(x). Абсциси точок перетину графіків y  =
= 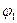 (х) і у
(х) і у  =
= 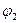 (х) будуть шуканими коренями(рис.1).
(х) будуть шуканими коренями(рис.1).
ПРИКЛАД: Виділити графічним методом корені рівняння
е 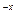 + х
+ х 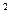 -2=0.
-2=0.
РОЗВ`ЯЗОК: Перепишемо дане рівняння у вигляді е 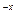 =2- х
=2- х 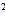 і розглянемо дві функції
і розглянемо дві функції 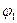 (х)=е
(х)=е 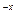 і
і 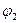 (х)=2- х
(х)=2- х 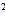 . Точки перетину графіків цих функцій і є коренями заданого рівняння (рис.2). Як видно із рисунка, задане рівняння має два дійсних кореня (графіки перетинаються в двох точках), причому один з коренів від`ємний, а другий – додатній. Обидва корені по абсолютній величині не перевищують
. Точки перетину графіків цих функцій і є коренями заданого рівняння (рис.2). Як видно із рисунка, задане рівняння має два дійсних кореня (графіки перетинаються в двох точках), причому один з коренів від`ємний, а другий – додатній. Обидва корені по абсолютній величині не перевищують 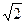 (-
(- 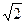 <x
<x  <0, 0<x
<0, 0<x  <
< 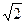 ).
).
Цей метод полягає в тому, що наугад вибирають точку х=а із області визначення функції (або із більш вузчої області), знаходять знак f(a), а потім підбирають точку b так, щоб значення функції f(b) мало знак, протилежний знаку f(a). Далі визначають знак f  (x) всередині відрізка [a;b]. Якщо f
(x) всередині відрізка [a;b]. Якщо f  (x) не міняє знак на [a;b], то корінь виділений, в інакшому випадку відрізок [a;b] звужують, взяв точку с, яка лежить посередині відрізка [a;b]. Визначають знак f(c) і в якості нового відрізка розглядають або [a;c] (якщо f(a)*f(c)<0), або [c;b] (якщо f(c)*f(a)<0). Позначивши новий відрізок через [a
(x) не міняє знак на [a;b], то корінь виділений, в інакшому випадку відрізок [a;b] звужують, взяв точку с, яка лежить посередині відрізка [a;b]. Визначають знак f(c) і в якості нового відрізка розглядають або [a;c] (якщо f(a)*f(c)<0), або [c;b] (якщо f(c)*f(a)<0). Позначивши новий відрізок через [a  ;b
;b  ], повторяють ті самі дії, що на відрізку [a;b], до тих пір, поки не буде знайдено відрізок [a
], повторяють ті самі дії, що на відрізку [a;b], до тих пір, поки не буде знайдено відрізок [a  ;b
;b  ], який визначає корінь .
], який визначає корінь .
ПРИКЛАД: Методом проб виділити додатній корінь рівняння:
х 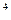 + х
+ х  -36х-20=0.
-36х-20=0.
РОЗВ`ЯЗОК: Функція f(x)= х 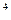 + х
+ х  -36х-20 визначена на всій числовій прямій. Оскільки треба виділити додатній корінь рівняння, розглянемо пів інтервал [0;
-36х-20 визначена на всій числовій прямій. Оскільки треба виділити додатній корінь рівняння, розглянемо пів інтервал [0; 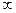 ].
].
1. 1. Знаходимо f(0)=-20<0. Потім вибираємо будь-яку точку, наприклад х=1, і обчислюємо f(1)=-54<0. Так як f(0)*f(1)>0, то нічого визначеного про відрізок [0;1] сказати не можна. Треба підібрати так точку х=b, щоб було f(b)>0, а для цього х 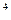 + х
+ х  повинно бути більше, чим 36х+20. Візьмемо, наприклад, х=4, тоді f(4)=156>0, а відповідно, на відрізку [1;4] є корінь (f(1)*f(4)<0).
повинно бути більше, чим 36х+20. Візьмемо, наприклад, х=4, тоді f(4)=156>0, а відповідно, на відрізку [1;4] є корінь (f(1)*f(4)<0).
2. 2. Оскільки f  (x)=4х
(x)=4х  +3x
+3x 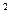 -36=4(х
-36=4(х  -9)+3x
-9)+3x 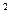 , то безпосередньою перевіркою переконуємося , що на відрізку [1;4] похідна міняє знак (f
, то безпосередньою перевіркою переконуємося , що на відрізку [1;4] похідна міняє знак (f  (1)=-29<0; f
(1)=-29<0; f  (4)=268>0).
(4)=268>0).
Звужаємо відрізок [1;4]. Візьмемо, наприклад, точку х=3. Тоді f(3)=-20<0 і f(3)*f(4)<0. Відповідно на відрізку [3;4] є корінь. Перевіряємо знак похідної. Маємо f  (3)=99>0, а для х>3, очевидно, похідна зростає, тому залишається додатною. Таким чином, корінь виділений. На відрізку [3;4] знаходиться додатній дійсний корінь заданого рівняння. Відмітимо, що f
(3)=99>0, а для х>3, очевидно, похідна зростає, тому залишається додатною. Таким чином, корінь виділений. На відрізку [3;4] знаходиться додатній дійсний корінь заданого рівняння. Відмітимо, що f  (x)=12x
(x)=12x 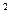 +6x>0 для хЄ[3;4]. Графік y=f(x) для хЄ[3;4] має приблизно такий же вигляд, як на рис.1.
+6x>0 для хЄ[3;4]. Графік y=f(x) для хЄ[3;4] має приблизно такий же вигляд, як на рис.1.
Цей метод полягає в тому, що спочатку визначаємо інтервали монотонності функції f(x) (якщо це не складно), тобто інтервали області визначення функції, в яких похідна зберігає знак. Потім обчислюємо знаки функції на кінцях цих інтервалів і визначаємо інтервал (а;b), на якому похідна зберігає знак і f(a)*f(b)<0. Задача виділення кореня виконана. Таким способом можна виділити всі дійсні корені рівняння f(x)=0.
Якщо ж серед інтервалів монотонності функції не існує інтервала, на кінцях якого функція має різні знаки, то це означає, що або рівняння f(x)=0 не має дійсних коренів, або такими являються границі інтервалів монотонності, тобто для цих точок функція і похідна цієї функції рівні нулю(див. рис.1, точка х  ). Це так називаємі кратні корені.
). Це так називаємі кратні корені.
ПРИКЛАД: Виділити дійсні корені рівняння
x-sinx-1=0.
РОЗВ`ЯЗОК: Розглянемо функцію f(x)= x-sinx-1, яка визначена на всій числовій прямій.
1. 1. Знаходимо першу похідну і інтервали монотонності функції. Одержимо f  (x)=1-cosx, звідси 1-cosx=0,
(x)=1-cosx, звідси 1-cosx=0,
cos x=1, х=2 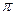 n(n=Z),
n(n=Z),
так, що інтервалами монотонності функції являються всі інтервали виду (2 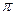 n; 2
n; 2 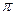 (n+1)).
(n+1)).
2. 2. Визначаємо знаки функції в граничних точках інтервалів монотонності. Взявши відрізок [0;2 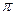 ], знаходимо f(0)=-1<0, f(2
], знаходимо f(0)=-1<0, f(2 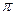 )=2
)=2 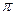 -1>0 і переконуємося, що на цьому відрізку є один корінь рівняння. По вигляду функції заключаєм, що для х>2
-1>0 і переконуємося, що на цьому відрізку є один корінь рівняння. По вигляду функції заключаєм, що для х>2 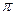 буде f(x)>0 (так як sinx<=1 і х>sinx+1), а для х<0 буде f(x)<0 ( так як sinx>=1 і sinx>x-1). Відповідно, в інших інтервалах монотонності функція знаку не міняє. Рівняння має єдиний корінь, що знаходиться на відрізку [0; 2
буде f(x)>0 (так як sinx<=1 і х>sinx+1), а для х<0 буде f(x)<0 ( так як sinx>=1 і sinx>x-1). Відповідно, в інших інтервалах монотонності функція знаку не міняє. Рівняння має єдиний корінь, що знаходиться на відрізку [0; 2 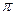 ].
].
Враховуючи ще умову 3), знаходимо f  (x)=sin x, яка на відрізку[0;2
(x)=sin x, яка на відрізку[0;2 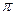 ] міняє знак. Відрізком, що виділяє корінь, буде [0;
] міняє знак. Відрізком, що виділяє корінь, буде [0; 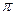 ], оскільки
], оскільки
1) 1) f(0)=-1, f( 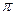 )=
)= 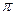 -1, f(0)* f(
-1, f(0)* f( 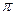 )<0;
)<0;
2) 2) перша похідна не міняє знаку на [0; 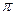 ];
];
3) 3) друга похідна не міняє знаку на [0; 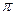 ];
];
Нехай на відрізку [a;b] виділений корінь рівняння f(x)=0, тоді в якості наближеного значення кореня х  може бути прийнята будь-яка точка х, що лежить всередині [a;b]. Ясно, що чим менший відрізок, тим точніше х буде представляти корінь х
може бути прийнята будь-яка точка х, що лежить всередині [a;b]. Ясно, що чим менший відрізок, тим точніше х буде представляти корінь х 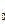 . Для того, щоб вважати х цілком сприйнятливим, оцінимо різницю
. Для того, щоб вважати х цілком сприйнятливим, оцінимо різницю 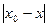 , тобто різницю між точним і наближеним значеннями кореня. Очевидно, що
, тобто різницю між точним і наближеним значеннями кореня. Очевидно, що 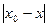 < b-a, так як х
< b-a, так як х  і х знаходяться всередині [a;b]. Число b-a являється оцінкою наближеного значення х:
і х знаходяться всередині [a;b]. Число b-a являється оцінкою наближеного значення х:  (х)= b-a. Найчастіше в якості х вибираємо точку, що лежить посередині відрізка [a;b], тобто х=
(х)= b-a. Найчастіше в якості х вибираємо точку, що лежить посередині відрізка [a;b], тобто х= 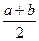 , тоді помилка при заміні х
, тоді помилка при заміні х 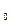 на х буде не більше чим
на х буде не більше чим 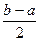 , тобто
, тобто  (х)=
(х)= 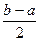 , причому, по знаках f(a), f
, причому, по знаках f(a), f 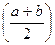 , f(b) з`ясовуємо, в якому із відрізків
, f(b) з`ясовуємо, в якому із відрізків 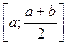 чи
чи 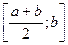 знаходиться шуканий корінь. Однак стверджувати, що значення х=
знаходиться шуканий корінь. Однак стверджувати, що значення х= 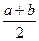 точніше представляє корінь, чим, наприклад, значення х=а, не має ніяких підстав. Вказані оцінки являються достатньо грубими і не залежать від розглядуваної функції, а лише від довжини відрізка [a;b].
точніше представляє корінь, чим, наприклад, значення х=а, не має ніяких підстав. Вказані оцінки являються достатньо грубими і не залежать від розглядуваної функції, а лише від довжини відрізка [a;b].
Для уточнення оцінки наближеного значення х кореня х  використаємо формулу скінчених приростів Лагранжа:
використаємо формулу скінчених приростів Лагранжа:
f(х  )-f(x)=f
)-f(x)=f  (
( 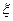 )( х
)( х  -x),
-x),
де 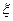 -деяка точка між х
-деяка точка між х 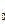 і х. Так як х
і х. Так як х 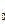 - корінь рівняння, то f(х
- корінь рівняння, то f(х  )=0 і тоді
)=0 і тоді 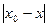 =
=  .
.
Згідно припущенню, f  (х)
(х)  0 і неперервна на [a;b], а тоді існує таке m>0, що
0 і неперервна на [a;b], а тоді існує таке m>0, що 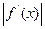
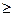 m для хЄ[a;b], тобто
m для хЄ[a;b], тобто 
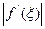
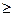 m і
m і 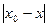
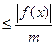 , відповідно,
, відповідно, 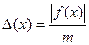 .
.
Замітимо, що якщо b-a менше, чим величина 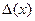 , то оцінкою буде менше число, тобто
, то оцінкою буде менше число, тобто 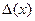 =min
=min 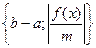 .
.
ПРИКЛАД: Оцініть наближене значення кореня, виділеного в прикладі методі проб.
РОЗВ`ЯЗОК: В прикладі було виділено, що шуканий корінь знаходиться на відрізку [3;4], відповідно, b-a=1.
Приймемо за наближене значення кореня число х=b=4. Тоді f(х)= f(4)=156. Як вказано в прикладі, f  (x)
(x) 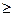 f
f  (3)=99,
(3)=99,  (4)=
(4)= 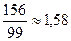 . Але, b-a=1<1,58, а відповідно,
. Але, b-a=1<1,58, а відповідно,  (4)=min
(4)=min 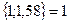 , і 3
, і 3 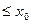
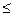 4. Якщо в якості х взяти, наприклад,
4. Якщо в якості х взяти, наприклад, 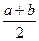 =3,5, то f(3,5)
=3,5, то f(3,5) 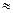 47>0. Корінь х
47>0. Корінь х 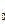 виділений на відрізку[3;3,5]. Оцінка наближення х=3,5 буде
виділений на відрізку[3;3,5]. Оцінка наближення х=3,5 буде  . Накінець, при х=3,2 одержимо: f(3,2)
. Накінець, при х=3,2 одержимо: f(3,2) 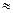 2,42>0; [3;3,2]- відрізок, що відділяє корінь, і
2,42>0; [3;3,2]- відрізок, що відділяє корінь, і 
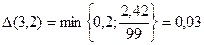 . Відповідно, можна вважати, що х
. Відповідно, можна вважати, що х 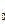 =3,2.
=3,2.
Якщо оцінка одержаного наближеного значення кореня задовольняє потрібні точності, то задачу можна вважати розв`язаною, в інакшому випадку треба перейти до обчислення або уточнення кореня з заданою точністю. 
Лекція 2: Методи послідовних наближень
1.Суть методу послідовних наближень
2.Метод хорд
3.Метод дотичних
4.Комбінований метод
5.Метод половинного поділу
6.Метод простої ітеракції
1.Суть методу послідовних наближень. Нехай виконана задача виділення кореня, тобто одержано відрізок [a;b] такий, що a<x 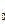 <b. Ясно, що чим менший відрізок [a;b], тим точніше вибране значення х (a<x<b) буде представляти корінь x
<b. Ясно, що чим менший відрізок [a;b], тим точніше вибране значення х (a<x<b) буде представляти корінь x  рівняння f(x)=0. Даль ніша задача полягає в послідовному звуженню відрізка [a;b] до тих пір, поки не одержимо значення кореня з заданою точністю. Ідея методу полягає в тому, що спочатку вибираємо деяку точку с
рівняння f(x)=0. Даль ніша задача полягає в послідовному звуженню відрізка [a;b] до тих пір, поки не одержимо значення кореня з заданою точністю. Ідея методу полягає в тому, що спочатку вибираємо деяку точку с  із [a;b] (перше наближення до x
із [a;b] (перше наближення до x 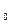 ), шуканий корінь при цьому попадає або в [a;с
), шуканий корінь при цьому попадає або в [a;с  ], або в [с
], або в [с  ;b]. Позначимо новий відрізок, виділяючий корінь, через
;b]. Позначимо новий відрізок, виділяючий корінь, через 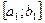 (очевидно, що
(очевидно, що 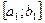 міститься в [a;b]), вибираємо в ньому точку с
міститься в [a;b]), вибираємо в ньому точку с  (друге наближення до x
(друге наближення до x 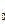 ) і знову звужуємо відрізок
) і знову звужуємо відрізок 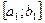 , замінивши його на
, замінивши його на 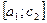 або на
або на 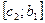 і так далі ., до тих пір, поки не одержимо відрізок
і так далі ., до тих пір, поки не одержимо відрізок 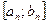 , в якому для вибраної точки
, в якому для вибраної точки 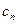 (n-го наближення) маємо
(n-го наближення) маємо 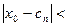 Е, де Е- задана точність наближення. Таким чином будуємо послідовність значень
Е, де Е- задана точність наближення. Таким чином будуємо послідовність значень 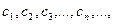 які повинні поступово наближатись до шуканого кореня. Тому цей метод називають методом послідовних наближень або ітераціонним процесом. Потім треба показати, щоlim c
які повинні поступово наближатись до шуканого кореня. Тому цей метод називають методом послідовних наближень або ітераціонним процесом. Потім треба показати, щоlim c 
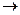 x
x 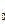
n 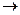
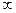 ,
,
а якщо це так, то ітераціонний процес називають збіжним.В цьому випадку x 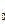 можна визначити з будь-якою заданою точністю.
можна визначити з будь-якою заданою точністю.
Існують різні методи послідовних наближень при відшуканні дійсних коренів рівняння.
2.Метод хорд. Найбільш простим із цих методів являється метод проб. Однак в цьому методі не враховуються особливості функції і тому можливі надто великі обчислення.
 Ідея методу полягає в тому, що на відрізку [a,b] будується хорда АВ, що стягує кінці дуги графіка функції y=f(x), і в якості наближеного значення кореня х
Ідея методу полягає в тому, що на відрізку [a,b] будується хорда АВ, що стягує кінці дуги графіка функції y=f(x), і в якості наближеного значення кореня х  вибирається число с=с
вибирається число с=с  , що являється абсцисою точки перетину цієї хорди з віссю ох (рис.1). Для визначення числа с
, що являється абсцисою точки перетину цієї хорди з віссю ох (рис.1). Для визначення числа с  складемо рівняння хорди як прямої, що проходить через дві точки А(a;f(a)) і В(b;f(b)):
складемо рівняння хорди як прямої, що проходить через дві точки А(a;f(a)) і В(b;f(b)):
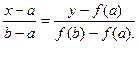
Взявши у=0, х=с  , одержимо
, одержимо
с  =а-
=а- 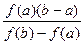 або
або 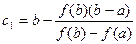
Число с  приймаємо за перше наближення до шуканого кореня .
приймаємо за перше наближення до шуканого кореня .
Очевидно, що при зроблених наближеннях про знаки першої і другої похідних на [a,b] точка (с  ;0) буде знаходитися зі сторони вгнутості кривої і розділить [a,b] на два відрізки [a;c
;0) буде знаходитися зі сторони вгнутості кривої і розділить [a,b] на два відрізки [a;c  ] і [c
] і [c  ;b], в одному з яких знаходиться корінь х
;b], в одному з яких знаходиться корінь х  (рис.1). Новий відрізок, виділяющий корінь, можна визначити, порівнюючи знаки f(a), f(c
(рис.1). Новий відрізок, виділяющий корінь, можна визначити, порівнюючи знаки f(a), f(c  ) і f(b). Із аналізу рис.1 видно, що точка с
) і f(b). Із аналізу рис.1 видно, що точка с  ближче до точки а, чим х
ближче до точки а, чим х  , якщо
, якщо  >0 (див. рис.1а), і відрізком, виділяющим корень, буде [c
>0 (див. рис.1а), і відрізком, виділяющим корень, буде [c  ;b], в іншому випадку, якщо
;b], в іншому випадку, якщо  <0 (див. рис.2б), відрізком, виділяющим корінь, буде [a;c
<0 (див. рис.2б), відрізком, виділяющим корінь, буде [a;c  ].
].
Далі повторимо ту ж процедуру на новому відрізку, виділяющим корень, і визначаєм число с  (друге наближення) по формулах:
(друге наближення) по формулах:
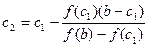 (
(  >0),
>0),
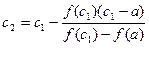 (
(  <0).
<0).
Потім по с  знаходимо с
знаходимо с 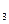 і так далі ( див. рис.1)
і так далі ( див. рис.1)
Процес призупиняється тоді, коли оцінка одержаного наближення задовольняє заданій точності.
Для спрощення обчислень часто задають деяке достатньо мале число Е>0 ( не більше заданої точності). Процес зупиняється тоді, коли абсолютна величина різниці між двома наступними наближеннями с 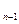 і с
і с  менше Е. Число с
менше Е. Число с  приймають за наближене значення кореня, тобто х= с
приймають за наближене значення кореня, тобто х= с  .
.
ПРИКЛАД: Використовуючи метод хорд, уточнити корінь рівняння х 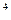 + х
+ х  -36х-20=0, який виділений на відрізку [3;4] (див. приклад методу проб). Обмежитись трьома наближеннями.
-36х-20=0, який виділений на відрізку [3;4] (див. приклад методу проб). Обмежитись трьома наближеннями.
РОЗВ`ЯЗАННЯ: Згідно умови, маємо f(x)= х 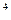 + х
+ х  -36х-20, f
-36х-20, f  (x)=4х
(x)=4х  +3x
+3x 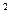 -36, f
-36, f  (x)=12x
(x)=12x 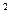 +6x і хЄ[3;4].
+6x і хЄ[3;4].
Уточнення кореня буде проходити по алгоритму:
1. 1. Для хЄ[3;4] маємо f  (x)>0, f
(x)>0, f  (x)>0, так що
(x)>0, так що  >0, відповідно, вводимо позначення с
>0, відповідно, вводимо позначення с  =а=3, А=b=4. Знаходимо f(А)= f(4)=156.
=а=3, А=b=4. Знаходимо f(А)= f(4)=156.
2. 2. Обчислюємо перше наближення 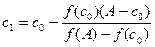 .
.
Для цього послідовно визначаємо A-c  =1, f(c
=1, f(c  )=f(3)=-20, f(A)-f(c
)=f(3)=-20, f(A)-f(c  )=176,
)=176,
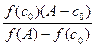
 -0,1136. Тоді с
-0,1136. Тоді с  =3-(-0,1136)=3,1136.
=3-(-0,1136)=3,1136.
Обчислюємо с  - друге наближення.
- друге наближення. 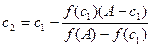 , с
, с  =3,1564
=3,1564
Третє наближення 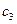 =3,1719.
=3,1719.
Отже, шуканий корінь знаходиться на відрізку [3,1719;4].
Обґрунтування методу хорд. Впевнимося, що послідовне застосування методу дозволяє визначити х  з будь-якою заданою точністю. Відмітимо, що послідовність с
з будь-якою заданою точністю. Відмітимо, що послідовність с 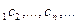 монотонно змінюється і обмежена. Дійсно, при
монотонно змінюється і обмежена. Дійсно, при  >0 маємо с
>0 маємо с  <c
<c  <…<c
<…<c 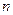 <…< х
<…< х  (див. рис.1а)), а при
(див. рис.1а)), а при  <0 маємо с
<0 маємо с  >c
>c  >…>c
>…>c 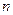 >…>х
>…>х  (див. рис.1б)). Тут істотно, що друга похідна не міняє знаку на відрізку. Згідно теореми із теореми границь, така послідовність має границю
(див. рис.1б)). Тут істотно, що друга похідна не міняє знаку на відрізку. Згідно теореми із теореми границь, така послідовність має границю  . Перейшовши до границі в формулі
. Перейшовши до границі в формулі 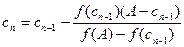 і використавши неперервність f(x), одержимо:
і використавши неперервність f(x), одержимо:
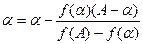 ,
, 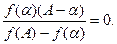
Звідси f(  )=0, так як А
)=0, так як А 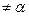 , f(А)
, f(А) 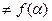 . Отже,
. Отже,  є коренем рівняння f(х)=0, але на відрізку [a;b] існує один корінь рівняння, отже,
є коренем рівняння f(х)=0, але на відрізку [a;b] існує один корінь рівняння, отже, 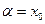 . Так що послідовні наближення збігаються до кореня х
. Так що послідовні наближення збігаються до кореня х  .
.
Оцінка одержаних наближень: 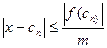 , де m- найменше значення модуля похідної на відрізку.
, де m- найменше значення модуля похідної на відрізку.
Покажемо, що при зроблених припущеннях про похідну на відрізку m= 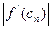 .
.
Нехай  >0, тоді відрізки, в яких знаходиться корінь, мають вигляд [c
>0, тоді відрізки, в яких знаходиться корінь, мають вигляд [c  ;b]. Якщо у
;b]. Якщо у  >0 і у
>0 і у  >0, то перша похідна зростає і додатня, відповідно, найменше її значення в лівому кінці відрізка, тобто m=
>0, то перша похідна зростає і додатня, відповідно, найменше її значення в лівому кінці відрізка, тобто m= 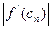 =f
=f  (c
(c  ); при у
); при у  <0, у
<0, у  <0 перша похідна спадає (а по абсолютній величині зростає) і найменше значення її модуля знову досягається в лівому кінці відрізка, тобто m=
<0 перша похідна спадає (а по абсолютній величині зростає) і найменше значення її модуля знову досягається в лівому кінці відрізка, тобто m= 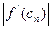 =-f
=-f 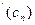 .
.
Аналогічно розглядаємо при  <0, беручи відрізки [a;c
<0, беручи відрізки [a;c  ]. Відповідно,
]. Відповідно, 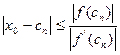 і
і 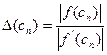 (*)
(*)
Вернемось до розв`язування прикладу і використаємо формули(*).
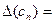 0,009; с
0,009; с  =3,1719 відрізняється від х
=3,1719 відрізняється від х  не більше чим на 0,009. Оскільки с
не більше чим на 0,009. Оскільки с  в даному прикладі наближається до кореня зліва (див. рис. 1а)), то 3,172<x
в даному прикладі наближається до кореня зліва (див. рис. 1а)), то 3,172<x  <3,181.
<3,181.
Примітка: Для спрощення розрахунків в формулі * 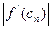 можна замінити на
можна замінити на 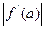 , якщо
, якщо  >0, і на
>0, і на 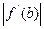 , якщо
, якщо  <0, тобто
<0, тобто 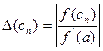 , якщо
, якщо  >0, і
>0, і 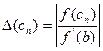 , якщо
, якщо  <0. При такій заміні оцінка буде грубшою, але обчислення простіші.
<0. При такій заміні оцінка буде грубшою, але обчислення простіші.
3.Метод дотичних. Ідея методу полягає в тому, що в одному із кінців дуги АВ графіка функції y=f(x) проводиться дотична до цієї дуги і в якості наближеного значення кореня х  вибирається число d
вибирається число d  (перше наближення)- абсциса точки перетину цієї дотичної з віссю ох (рис. 1). Як відомо рівняння дотичної до кривої y=f(x) в точці (x
(перше наближення)- абсциса точки перетину цієї дотичної з віссю ох (рис. 1). Як відомо рівняння дотичної до кривої y=f(x) в точці (x  ;f(x
;f(x 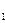 )) має вигляд y-f(x
)) має вигляд y-f(x  )=f
)=f 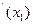 (x-x
(x-x  ). Відповідно, y-f(a)=f
). Відповідно, y-f(a)=f  (a)(x-a) – рівняння дотичної в точці А(a;f(a)), a y-f(b)=f
(a)(x-a) – рівняння дотичної в точці А(a;f(a)), a y-f(b)=f  (b)(x-b) – в точці B(b;f(b). Поклавши у=0, а х=d
(b)(x-b) – в точці B(b;f(b). Поклавши у=0, а х=d  , визначаємо абсцису точки перетину дотичної з віссю ох:
, визначаємо абсцису точки перетину дотичної з віссю ох: 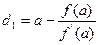 або
або 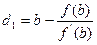 .
.
Очевидно, що точка (d  ;0) буде знаходиться зі сторони випуклості кривої. Точка d
;0) буде знаходиться зі сторони випуклості кривої. Точка d  розділить [a;b] на два відрізки [a;d
розділить [a;b] на два відрізки [a;d  ] і [d
] і [d  ;b], в одному із яких розміщена точка х
;b], в одному із яких розміщена точка х  . Якщо у
. Якщо у  у
у  >0, це буде відрізок [a;d
>0, це буде відрізок [a;d  ] (дотична проводиться в точці В, див. рис.1а), а при у
] (дотична проводиться в точці В, див. рис.1а), а при у  у
у  <0- відрізок [d
<0- відрізок [d  ;b](дотична проводиться в точці А, див. рис.1б). Визнавши новий виділяющий проміжок, процедуру повторяємо. При цьому дотичну проводимо в точці (d
;b](дотична проводиться в точці А, див. рис.1б). Визнавши новий виділяющий проміжок, процедуру повторяємо. При цьому дотичну проводимо в точці (d  ;f(d
;f(d  )) (див. рис.1) і визначаємо друге наближення - точку d
)) (див. рис.1) і визначаємо друге наближення - точку d  по формулі:
по формулі: 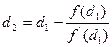 .
.
Потім по d  знаходимо третє наближення d
знаходимо третє наближення d 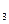 і т.д. Процес призупиняється тоді, коли абсолютна величина різниці двох наступних наближень d
і т.д. Процес призупиняється тоді, коли абсолютна величина різниці двох наступних наближень d 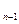 і d
і d  менше заданого Е>0, тобто
менше заданого Е>0, тобто 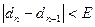 , і покладемо, що х=d
, і покладемо, що х=d  (число Е не перевищує заданої точності наближення і служить сигналом для зупинення обчислень).
(число Е не перевищує заданої точності наближення і служить сигналом для зупинення обчислень).
ПРИКЛАД: Користуючись методом дотичних, уточнити корінь рівняння 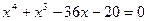 , який виділений на відрізку [3;4]. Обмежитись трьома наближеннями(див. приклад з методу хорд).
, який виділений на відрізку [3;4]. Обмежитись трьома наближеннями(див. приклад з методу хорд).
Розв`язок: Згідно умови, маємо f(x)= х 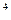 + х
+ х  -36х-20, f
-36х-20, f  (x)=4х
(x)=4х  +3x
+3x 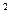 -36, f
-36, f  (x)=12x
(x)=12x  +6x і х
+6x і х  Є[3;4]. Уточнення кореня будем проводити по алгоритму.
Є[3;4]. Уточнення кореня будем проводити по алгоритму.
1.Для хЄ[3;4] буде у  у
у  >0, так що покладаєм d
>0, так що покладаєм d  =b=4.
=b=4.
2а). Маємо нульове наближення d  . Визначаємо перше наближення d
. Визначаємо перше наближення d  по формулі
по формулі 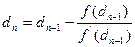 (*) при n=1:
(*) при n=1: 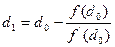 .
.
Послідовно находимо, що f(d  )=f(4)=156, f
)=f(4)=156, f 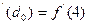 =268,
=268, 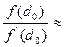 0,5821, і d
0,5821, і d 
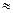 4-0,5821=3,4179.
4-0,5821=3,4179.
2б). Обчислюємо d  - друге наближення. Кладучи в формулі(*) n=2, знаходимо
- друге наближення. Кладучи в формулі(*) n=2, знаходимо 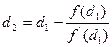 . Виконуючи відповідні обчислення, одержимо d
. Виконуючи відповідні обчислення, одержимо d  =3,2078.
=3,2078.
2в). Аналогічно по формулі(*) при n=3 знаходимо третє наближення 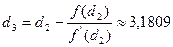 .
.
Обґрунтування методу дотичних. Покажемо, що послідовність 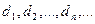 збігається і має своєю границею значення кореня х
збігається і має своєю границею значення кореня х  . Відмітимо, що при у
. Відмітимо, що при у  у
у  >0 маємо
>0 маємо 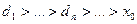 (див. рис. 1а), а при у
(див. рис. 1а), а при у  у
у  <0 маємо
<0 маємо 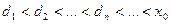 (див. рис 1б). При цьому послідовність
(див. рис 1б). При цьому послідовність 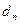 прямує до
прямує до  при n прямує до нескінченості (послідовність
при n прямує до нескінченості (послідовність 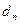 монотонно міняється і обмежена). Переходячи до границі в формулі (*) і використовуючи неперервність f(x) і f
монотонно міняється і обмежена). Переходячи до границі в формулі (*) і використовуючи неперервність f(x) і f  (x), як в методі хорд, знаходимо
(x), як в методі хорд, знаходимо 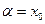 . Одержані наближення оцінюються по формулі
. Одержані наближення оцінюються по формулі 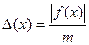 , причому
, причому 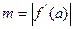 і
і 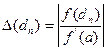 при у
при у  у
у  >0,
>0, 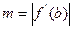 і
і 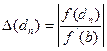 при у
при у  у
у  <0.
<0.
В розглянутому прикладі у  у
у  >0, тому оцінка кожного наближення обчислюється по формулі
>0, тому оцінка кожного наближення обчислюється по формулі 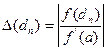 , де
, де 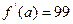 . Маємо
. Маємо 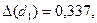

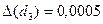 . Видимо, що для
. Видимо, що для 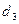 =3,1809 оцінка
=3,1809 оцінка 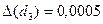 і наближення
і наближення 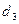 обчислене з трьома точними десятковими значеннями.
обчислене з трьома точними десятковими значеннями.
Оскільки числа 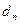 визначають в цьому випадку корінь х
визначають в цьому випадку корінь х  з недостачею, то 3,1804< х
з недостачею, то 3,1804< х  <3,1809.
<3,1809.
4.Комбінований метод. Ідея методу полягає в об`єднанні метода хорд і метода дотичних. Із рисунка 1 і попередніх описань цих методів видно, що наближення с  , обчислюване по методу хорд, прямує до кореня х
, обчислюване по методу хорд, прямує до кореня х  зі сторони вгнутості кривої, а наближення d
зі сторони вгнутості кривої, а наближення d  , обчислюване по методу дотичних,- зі сторони опуклості кривої. При цьому для будь-якого наближення маємо: с
, обчислюване по методу дотичних,- зі сторони опуклості кривої. При цьому для будь-якого наближення маємо: с  <x
<x  < d
< d  при у
при у  у
у  >0, d
>0, d  < x
< x  < с
< с  при у
при у  у
у  <0. Відповідно, комбінуючи ці два методи і визначаючи с
<0. Відповідно, комбінуючи ці два методи і визначаючи с  і d
і d  , послідовно на кожному кроці звужуємо з двох сторін відрізок, всередині якого знаходиться корінь x
, послідовно на кожному кроці звужуємо з двох сторін відрізок, всередині якого знаходиться корінь x  . Процес призупиняється тоді, коли
. Процес призупиняється тоді, коли 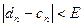 , де Е- задана точність обчислення.
, де Е- задана точність обчислення.
За наближене значення кореня частіше беремо точку, що належить середині відрізка, тобто х= 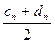 , так що
, так що 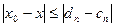 <E.
<E.
5.Метод половинного поділу. Метод половинного поділу також можна віднести до методу послідовних наближень. По своїй ідеї метод простий і фактично аналогічний методу проб, але його реалізація зв`язана з довгими обчисленнями ( великим числом ітерацій) і тому при ручних обчисленнях метод половинного поділу не застосовується. При використанні програмування цей метод набагато простіший, так як не потребує обмежуючих умов для першої і другої похідних.
Алгоритм методу половинного поділу. Нехай відомо, що на відрізку [a;b] знаходиться один єдиний корінь рівняння f(x)=0, відповідно, f(a)*f(b)<0. Треба визначити цей корінь з заданою точністю Е.
Суть методу полягає в тому, що відрізок [a;b] ділимо пополам точкою с  =
= 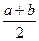 (перше наближення) і розглядаємо той із відрізків [a;c
(перше наближення) і розглядаємо той із відрізків [a;c  ] або [c
] або [c  ;b], який містить шуканий корінь. Позначимо цей відрізок через
;b], який містить шуканий корінь. Позначимо цей відрізок через 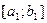 , причому
, причому 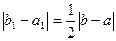 , визначаємо точку с
, визначаємо точку с 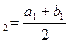 (друге наближення) і розглядаємо відрізок [a
(друге наближення) і розглядаємо відрізок [a  ;c
;c  ] або [c
] або [c  ;b
;b  ], що містить шуканий корінь, тобто [a
], що містить шуканий корінь, тобто [a  ;b
;b  ], де
], де  , і так далі, до тих пір, поки не одержимо відрізок [a
, і так далі, до тих пір, поки не одержимо відрізок [a 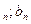 ], що містить шуканий корінь х
], що містить шуканий корінь х  , для якого
, для якого 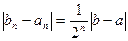 <E (*).
<E (*).
Точку с 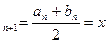 приймаємо за наближене значення кореня х
приймаємо за наближене значення кореня х  . Із (*) видно, що
. Із (*) видно, що 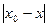 <0.
<0.
Із (*) можна наперед визначити число n послідовних наближень, необхідних для визначення кореня при заданім Е: n> 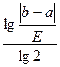 , або n=
, або n= 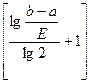 .
.
6.Метод простої ітеракції.
Розглянемо рівняння х= 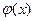 (0)
(0)
Нехай [a;b] – відрізок, що виділяє корінь х  цього рівняння, тобто х
цього рівняння, тобто х 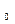 =
= 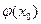 . Вибираємо довільну точку с
. Вибираємо довільну точку с  Є [a;b] і першим наближенням називаємо число с
Є [a;b] і першим наближенням називаємо число с  , де с
, де с  =
= 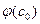 , по першому наближенню будуємо друге с
, по першому наближенню будуємо друге с 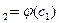 і так далі с
і так далі с 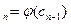 (1)
(1)
Таким чином будується послідовність наближень 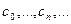 . Якщо ця послідовність збігається, причому с
. Якщо ця послідовність збігається, причому с  прямує до х
прямує до х  при n прямуючому до нескінченості, то за скінчене число ітеракцій буде одержано наближення с
при n прямуючому до нескінченості, то за скінчене число ітеракцій буде одержано наближення с  , яке представляє наближене значення кореня з заданою точністю Е, тобто
, яке представляє наближене значення кореня з заданою точністю Е, тобто 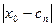 <E. Однак ітеракційний процес, що визначається формулою (1), не завжди збігається.
<E. Однак ітеракційний процес, що визначається формулою (1), не завжди збігається.
Вияснимо спочатку геометричний зміст процесу і його збіжності.
