Алгоритм критерия Пирсона

Исходя из вида кривой распределения 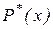выдвигается гипотеза
подчинения случайной величины закону распределения .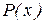

Таблица 3.9

Значения случайных чисел, равномерно

распределенных на интервале [0; 1]*

* Все значения, приведенные в таблице, увеличены в 10⁵ раз.

Сравнение эмпирического 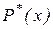и теоретического 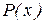распределений производится с помощью специально подобранной случайной величины – критерия 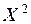(Пирсона) для нормального закона распределения.

Проверка выполняется по следующему алгоритму.

1) Для полученной выборки входных сопротивлений 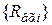определяют математическое ожидание

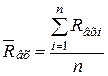(3.82)

и среднее квадратическое отклонение выборки

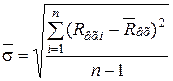. (3.83)

2) Для каждого интервала построенной гистограммы определяют середину 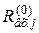и подсчитывают число попавших в него наблюдений .

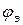3) Вычисляют число наблюдений для каждого из интервалов, теоретически соответствующее нормальному распределению. Для этого от реальных середин 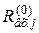интервалов переходят к нормированным:

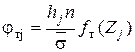; (3.84)

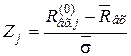. (3.85)

Вычисление 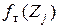ведется по табл. 3.10.

Если для некоторого интервала 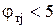, то интервал объединяется с соседним. Расчеты повторяются с п. 2 при L' <L (L' – число интервалов после объединения). Определяют число степеней свободы, равное
L' – 3.

4) Вычисляют показатель разности частот:

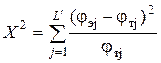. (3.86)

Таблица 3.10