Тема 9.Изгиб плоского бруса большой кривизны

В случае изгиба прямого стержня гипотеза плоских сечений приводит к линейному закону распределения нормальных напряжений. Применяя эту же гипотезу при изгибе кривого стержня, получаем гиперболический закон распределения нормальных напряжений в поперечном сечении стержня.

Другая важная особенность изгиба кривого стержня заключается в том, что нейтральная ось не совпадает с центром тяжести поперечного сечения и всегда смещается по направлению к центру кривизны.

После изучения этой темы можно решать задачу 12, включенную в контрольные работы.

Литература:[5, гл. 10]; [6, гл. 11, задачи: 1, 2, 7, 16, 18] ]; [7, гл. 14].

Вопросы для самопроверки

103. Как вычисляют изгибающие моменты, продольные и поперечные силы в поперечных сечениях кривого стержня?

104. Как находят касательные напряжения от силы Q?

105. Как находят нормальные напряжения в поперечном сечении кривого стержня от изгибающего момента М?

106. Где проходит нейтральная ось при изгибе кривого стержня?

107. Как находят радиус кривизны нейтрального слоя кривого стержня?

Тема 10.Устойчивость равновесия

Деформируемых систем

Предыдущие темы курса касались расчётов на прочность и на жёсткость. В этой теме изложен расчёт на устойчивость. Опасность явления потери устойчивости заключается в том, что оно может наступить при напряжении, значительно меньшем предела прочности материала. Это напряжение называется критическим; для стержней большой гибкости его можно определить по формуле Эйлера. Исследования профессора Ф.С. Ясинского дали возможность установить значение критического напряжения для стержней малой и средней гибкости, для которых формулу Эйлера применять нельзя. Допускаемое напряжение при расчёте на устойчивость должно быть понижено по сравнению с допускаемым напряжением при обыкновенном сжатии. Значения коэффициентов 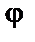, учитывающих это понижение для стержней различной гибкости и для различных материалов, приводятся в специальных таблицах. Следует обратить внимание на то, что при подборе сечения приходится несколько раз производить вычисления, применяя способ последовательных приближений.

После изучения этой темы можно решать задачу 13, включённую в контрольные работы.

Литература: [4, гл. 13]; [5, гл. 13]; [6, гл. 12, задачи: 2, 4, 11, 14, 32] ]; [7, гл. 15].

Вопросы для самопроверки

108. В чём заключается явление потери устойчивости сжатого стержня?

109. Какая сила называется критической?

110. Что называется гибкостью стержня?

111. Напишите формулуЭйлера для критической силы?

112. В каких пределах применима формула Эйлера?

113. Чему равен коэффициент приведения длины для различных случаев закрепления концов стержня?

114. Как изменится критическая сила при увеличении длины стойки в два раза?

115. Какой вид имеет полный график критических напряжений?

116. Как находят критическое напряжение для стержней малой и средней гибкости?

117. Как производится проверка стержней на устойчивость с помощью коэффициента ?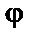

118. Как подбирают сечение стержня при расчёте на устойчивость?