Уточнення коренів. Метод проб

ЧИСЛОВЕ РОЗВ’ЯЗАННЯ РІВНЯНЬ З ОДНІЄЮ ЗМІННОЮ

Вступ

Електронні обчислювальні машини (ЕОМ) широко застосовуються для розв’язання наукових, технічних та економічних задач. Вони здатні виконувати обчислення дуже швидко, видавати точні результати, запам’ятовувати великі масиви інформації, здійснювати довгі та складні послідовності розрахунків без втручання людини. При цьому не зайвим буде додати, що ЕОМ не "розв’язує задачу". Вона допомагає лише розглядати різні варіанти досліджуваного питання.

ЕОМ не може задатися вихідними даними, перерахувати умови, за яких треба досліджувати роботу системи, визначати чи знаходити розумний ступінь компромісу між суперечливими критеріями.

Поняття "розв’язання задачі" з допомогою ЕОМ включає в себе набагато більше, ніж звичайні розрахунки на ЕОМ. Необхідно чітко розуміти, що робить людина і що робить машина.

Зазначимо, що процес розв’язання задачі з використанням ЕОМ в достатньо загальному випадку включає в себе наступні етапи:

1) постановка задачі та визначення кінцевих цілей;

2) побудова математичної моделі;

3) числовий аналіз;

4) програмування для ЕОМ;

5) налагодження програми;

6) розрахунки;

7) інтерпретація результатів.

Найбільш складним і відповідальним етапом розв’язання задачі є побудова математичної моделі. Цей етап вимагає повного розуміння проблеми та знання відповідних областей математики. Якщо обрана математична модель надто грубо відображає взаємозв’язки явища, що досліджується, то, які б витончені методи рішення не застосовувались, отримані результати не будуть відповідати умовам реальної задачі та виявляться марними. Математична модель може мати вигляд рівняння, системи рівнянь або бути вираженою в формі інших, як завгодно складних, математичних структур або співвідношень різної природи.

Числовий алгоритм розв’язання задачі необхідно виразити у вигляді точно визначеної послідовності операцій обчислювальної машини. Зазвичай ця робота виконується за дві стадії. На першій стадії послідовність операцій відображається графічно у вигляді блок-схеми. Потім розроблений алгоритм треба викласти мовою, зрозумілою обчислювальною машиною безпосередньо або після попереднього "перекладу".

Певні труднощі визиває етап розробки алгоритму, суть якого – пошук метода розв’язання задачі. Справа в тому, що навіть для достатньо простих моделей інколи не вдається отримати рішення в аналітичній формі. Наприклад, задача зведена до рішення рівняння з однією змінною

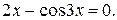
При всій тривіальності цієї задачі виразити корні цього рівняння шляхом аналітичних перетворень не вдається. Графічний метод бажаної точності не дає. У таких випадках доводиться використовувати числові методи, які дозволяють отримувати результати шляхом обчислень. З цієї причини найбільш природний шлях реалізації числових методів – використання ЕОМ.

Результати розрахунків, що видаються ЕОМ, не завжди мають повну "відповідь" до задачі. Людина, яка виконує розрахунки на ЕОМ, повинна якимось чином інтерпретувати результати, щоб зрозуміти, що вони означають з точки зору критеріїв, яким має задовольняти досліджувана система. Дуже часто доводиться частково або навіть повністю повторювати попередні етапи, поки задача не буде дійсно розв’язана.

Із цього стислого розгляду можна зробити деякі висновки. По-перше, ЕОМ сама задач не розв’язує, вона тільки виконує заздалегідь задані послідовності розрахунків. По-друге, використання ЕОМ не звільняє від необхідності ретельно осмислювати свою роботу. В дійсності використання ЕОМ примушує приділяти більше уваги осмислюванню розв’язуваних задач. Машина може виконувати розрахунки швидше і точніше людини, але вона не здатна приймати рішення відносно того, якою має бути програма розрахунків, а також, що робити з отриманими результатами. По-третє, ЕОМ жодним чином не знімає необхідності детального вивчення досліджуваної області та розділів математики, які застосовуються для розв’язання задачі.

Постановка задачі, визначення кінцевих цілей та математичний опис відносяться до відповідної галузі науки і техніки, а, отже, і інтерпретація результатів відносяться до тієї ж галузі науки чи техніки, що й вихідна задача.

Постановка задачі

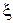Нехай f – поліном або трансцендентна функція однієї змінної, дійсної або комплексної. Будемо передбачати, що ця функція диференційована. Треба знайти один або більше нулів f, тобто розв’язків рівняння . Будь-яке число , яке обертає функцію в нуль, тобто таке, при якому 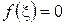, є коренем рівняння.

Число 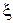називається коренем k-ї кратності, якщо при 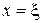разом з функцією дорівнюють нулю її похідні до порядку включно. Однократний корінь прийнято називати простим.

Нелінійні рівняння з однією змінною підрозділяються на алгебраїчні і трансцендентні. Рівняння називається алгебраїчним, якщо воно подається алгебраїчною функцією. Відомо, що алгебраїчне рівняння має як мінімум один корінь дійсний чи комплексний.

Якщо функція не є алгебраїчною, то вона називається трансцендентною.

Знаходження коренів рівняння є однією древніших математичних проблем, яка не втратила своєї гостроти і в наші дні. Вона часто зустрічається в різних галузях науки і техніки.

У загальному випадку, функції, корені яких будемо знаходити, не матимуть аналітичних формул для своїх коренів.

Оскільки значна кількість рівнянь з однією змінною не розв’язується шляхом аналітичних перетворень (точними методами), то на практиці їх розв’язують тільки числовими методами. Розв’язати таке рівняння – це значить визначити, чи має воно корені, скільки коренів існує, та знайти значення коренів з заданою точністю. Задача числового знаходження коренів рівняння 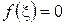зазвичай складається з двох етапів:

– відділення коренів, тобто знаходження достатньо малих околів області, що розглядається, в яких міститься одне значення кореня;

– уточнення коренів, тобто обчислення коренів з заданою точністю в деякій околиці.

Надалі будемо розглядати числові методи знаходження дійсних коренів рівняння 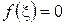. Найбільш поширеними на практиці числовими методами розв’язання таких рівнянь є: метод половинного ділення, метод хорд, метод дотичних (Ньютона), комбінований метод, метод простої ітерації. Застосування того чи іншого метода для розв’язання рівняння 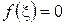залежить від числа коренів, задання вихідного наближення и поведінки функції, корені якою розшукуються.

Відділення коренів

Першим етапом числового розв’язання рівняння з однією змінною є відділення коренів, тобто визначення проміжків визначення функції, які містять тільки один корінь. Відділити корені – це значить розбити область допустимих значень функції на відрізки, в кожному із яких є один корінь.

Відділення коренів можна зробити двома способами – графічним і аналітичним.

Графічний спосіб відділення коренів. При графічному способі відділення коренів будують графік функції 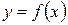для рівняння вигляду . Приймаючи до уваги, що дійсні корені рівняння 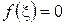– це точки перетину графіка цієї функції з віссю абсцис, тому достатньо побудувати графік і відмітити на осі Ох ділянки, які містять тільки один корінь.

Розглянемо графік функції 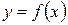, показаної на рис. 1. Цей графік тричі перетинає вісь абсцис. Отже рівняння має три простих корені. Крива, показана на рис. 2, торкається осі Ох. Отже вона описується рівнянням з двократним коренем.

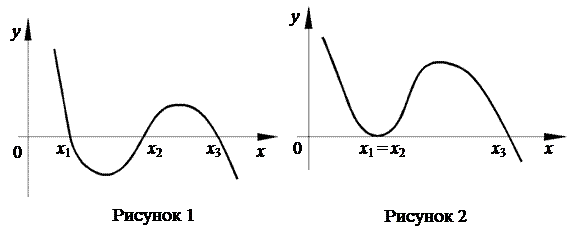Якщо крива подається рівнянням з трикратним дійсним коренем, то в місці торкання з віссю Ох вона має точку перегину (рис. 3).

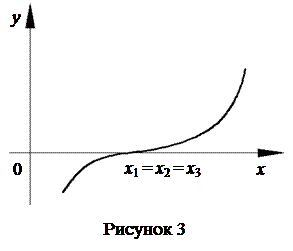Графічному методу відділення коренів не притаманна висока точність. Він дає можливість грубо визначити інтервали ізоляції кореня. У подальшому корені уточнюються одним із способів, що розглядаються нижче.

Аналітичний спосіб відділення коренів. Аналітично корені рівняння можна відділити, застосовуючи деякі властивості функцій, що вивчаються в курсі математичного аналізу.

Запишемо без доказу теореми, знання яких необхідні при відділенні коренів.

Теорема 1. Якщо функція неперервна на відрізку [А, B] і приймає на кінцях цього відрізка значення різних знаків, тобто 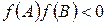, то всередині відрізка [А, B] існує принаймні один корінь рівняння , тобто значення х*, що .

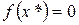Корінь х* буде єдиним на відрізку [А, B], якщо похідна 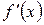існує та зберігає знак всередині інтервалу (А, B).

Теорема 2. Якщо функція неперервна і монотонна на відрізку [А, B] та приймає на кінцях цього відрізка значення різних знаків, то всередині відрізка [А, B] міститься корінь рівняння і до того ж єдиний.

Теорема 3. Якщо функція неперервна на відрізку [А, B] і приймає на кінцях цього відрізка значення різних знаків, а похідна 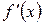зберігає постійний знак всередині відрізка, то всередині відрізка [А, B] корінь рівняння і до того ж єдиний.

Наведемо деякі відомості з математичного аналізу, які знадобляться в подальшому розумінні матеріалу.

Якщо функція задана аналітично, то областю існування (областю визначення) функції називається сукупність усіх тих дійсних значень аргументу, при яких аналітичний вираз, що визначає функцію, не втрачає числового сенсу і приймає тільки дійсні значення.

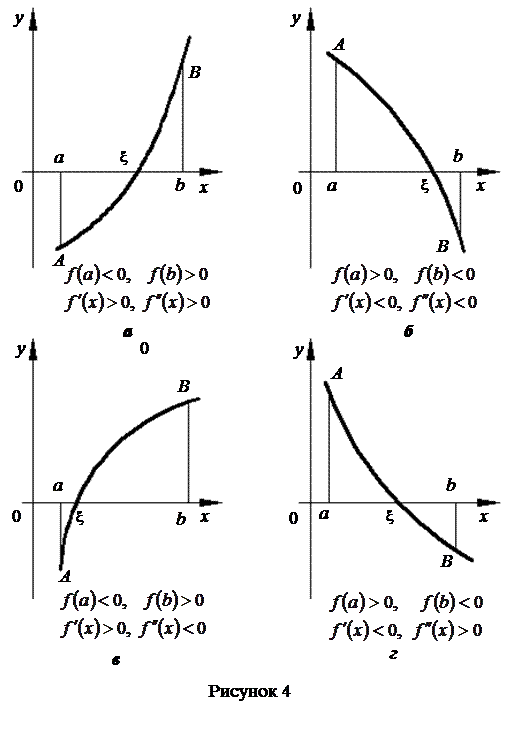
Функція називається зростаючою, якщо із зростання аргументу значення функції збільшується (рис. 4, а і в), і убиваючою, якщо із зростанням аргументу значення функції зменшується (рис. 4, б і г).

Функція називається монотонною, якщо вона в заданому проміжку або тільки зростає, або тільки убуває.

Нехай функція неперервна на відрізку [А, B] і приймає на кінцях цього відрізка значення різних знаків, а похідна 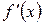зберігає постійний знак всередині інтервалу (A, B). Тоді якщо у всіх точках інтервалу (A, B) похідна додатна, тобто 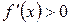, то функція у цьому інтервалі зростає (рис. 4, аі в).

Якщо ж у всіх точках інтервалу (a, b) перша похідна від’ємна, тобто 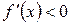, то функція у цьому інтервалі убуває (рис. 4, б і г). Коренем функції є абсциса точки перетину графіка функції з віссю Ох.

Нехай функція на відрізку [А, B] має похідну другого порядку, яка зберігає постійний знак на всьому відрізку. Тоді якщо 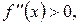то графік функції є опуклим униз (рис. 4, а і г); якщо 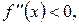то графік функції є опуклим уверх (рис. 4, б і в).

Точки, в яких перша похідна функції дорівнює нулю, а також ті, в яких вона не існує (наприклад, звертається в нескінченність), але функція зберігає неперервність, називаються критичними (ця ознака є необхідною ознакою екстремуму).

Якщо функція неперервна на відрізку [А, B], то на цьому відрізку завжди є точки, в яких вона приймає найбільше та найменше значення. Цих значень функція досягає або в критичних точках, або на кінцях відрізка. Отже, щоб визначити найбільше та найменше значення функції на відрізку треба:

1) визначити критичні точки функції;

2) обчислити значення функції в критичних точках і на кінцях відрізка [А, B];

3) найбільше із значень, знайдених у п. 2, буде найбільшим, а найменше – найменшим значенням функції на відрізку.

У зв’язку з вищевикладеним можна рекомендувати наступний порядок дій для відділення корнів аналітичним методом.

1. Знайти 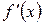– першу похідну.

2. Скласти таблицю знаків функції , приймаючи х рівним:

а) критичним значенням (кореням) похідної або найближчим до них;

б) граничним значенням (виходячи із області допустимих значень невідомого).

3. Визначити інтервали, на кінцях яких функція приймає значення протилежних знаків. Усередині цих інтервалів знаходиться по одному і тільки одному кореню.

Для відділення коренів можна ефективно використовувати ЕОМ.

Нехай маємо рівняння , при цьому можна вважати, що всі корені, які нас цікавлять, знаходяться на відрізку [А, B], де функція 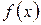визначена і непереривна та 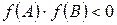. Треба відділити корені рівняння, тобто визначити всі відрізки [а, b] 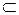[А, B], що містять по одному кореню.

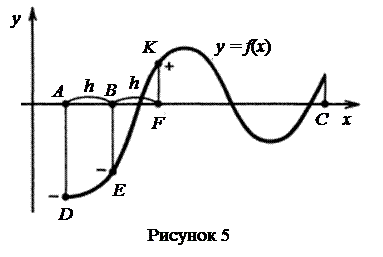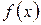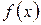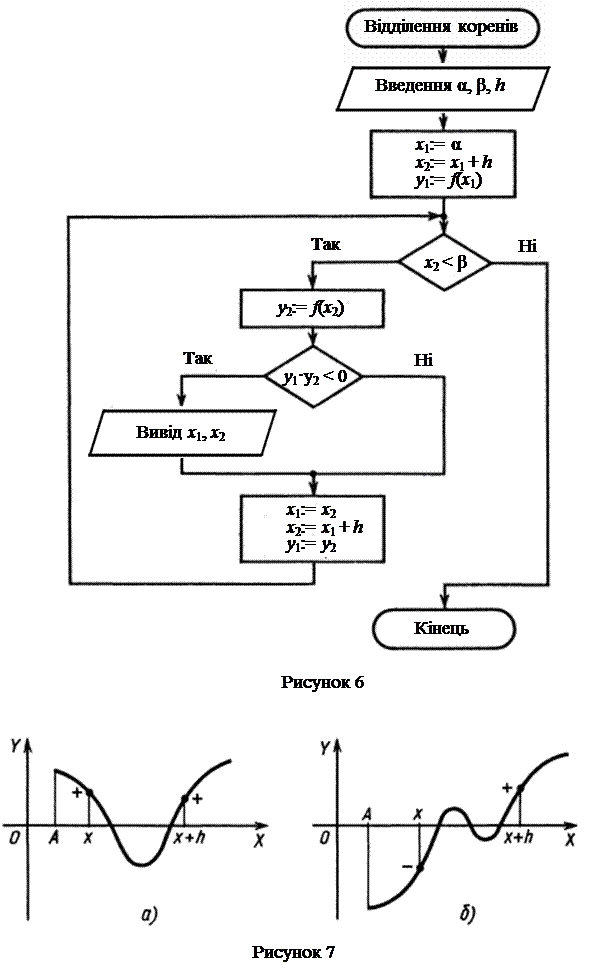
Будемо розраховувати значення , починаючи з точки х = А, рухаючись праворуч з деяким кроком h (рис. 5). Як тільки виявиться пара сусідніх значень , що мають різні знаки, і функція 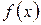монотонна на цьому відрізку, то відповідні значення аргументу х (попереднє і наступне)можна вважати кінцями відрізка, що містить корінь. Схема відповідного алгоритму зображена на рис. 6. Результатом розв’язання поставленої задачі буде виведення на екран монітора або на друк значень ідентифікаторів х₁ і х₂ (кінців виділених відрізків).

Очевидно, що надійність розглянутого підходу до визначення коренів рівнянь залежить як від характеру функції 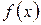, так і від вибраної величини кроку h. Дійсно, якщо при достатньо малому кроці h. на кінцях поточного відрізку [x, x + h] функція 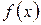приймає значення одного знаку, природно очікувати, що рівняння 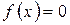коренів на цьому відрізку не має. Це, однак, не завжди так: при недотриманні умови монотонності функція 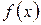на відрізку [x, x + h] можуть виявитися корені рівняння (рис. 7, а). Не один, а кілька коренів можуть виявитися на відрізку [x, x + h] і при дотриманні умови 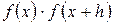(рис. 7, б). Передбачаючи подібні випадки, треба при відділені коренів вибирати достатньо малі значення h.

Уточнення коренів. Метод проб

Попередній підрозділ був присвячений першому з етапів наближеного розв’язання алгебраїчних і трансцендентних рівнянь – відділенню коренів.

Другий етап – уточнення коренів, тобто доведення їх до заданого ступеня точності.

Дано рівняння , де – неперервна функція. Треба знайти корінь цього рівняння 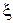з точністю до ε, де ε – деяке додатне достатньо мале число.

Вважатимемо, що корінь 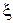відділений і знаходиться на відрізку [а, b], тобто має місце нерівність 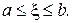Числа а і b є наближеними значеннями кореня відповідно з недостачею і з надлишком. Похибка цих наближень не перевищує довжини відрізка b – а. Якщо 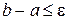, то бажана точність обчислень досягнута, і за наближене значення кореня 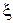можна прийняти або а, або b. 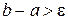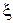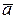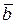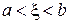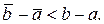Але якщо , то бажана точність обчислень не досягнута і необхідно звузити інтервал, в якому знаходиться корінь , тобто підібрати такі числа і , щоб виконувалася нерівність і При 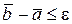обчислення треба зупинити і за наближене значення кореня з точністю до ε прийняти 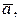або або 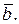Треба відмітити, що значення кореня буде більш точним, коли за наближене значення кореня прийняті не кінці відрізка 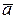і 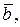а середина цього відрізка, тобто 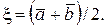Помилка при цьому не буде перевищувати величину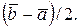

Метод проб. Нехай дано рівняння , де – неперервна функція, і корінь 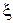відділений на відрізку [а, b], тобто 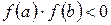, при чому 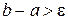. Треба знайти корінь цього рівняння 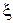з точністю до ε (рис. 8).

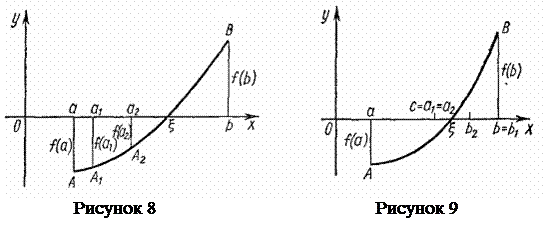На відрізку [а, b] вибирають довільним чином точку а₁, яка розділить його на два відрізки [а, а₁] і [а₁, b]. З цих двох відрізків вибирають той, на кінцях якого функція приймає значення з протилежними знаками. У нашому приклад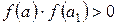і і 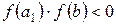, тому вибирають відрізок [а₁, b]. Потім на цьому звуженому відрізку знову довільним чином беруть точку а₂ і знаходять знаки добутків 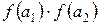і Оскільки 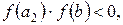то вибирають відрізок [а₂, b]. Цей процес продовжують до тих пір, поки довжина відрізка, на якому знаходиться корінь, не стане меншою ε. Корінь ξ отримують як середньоарифметичне значення кінців найденого відрізка, причому помилка кореню не перевищуватиме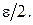

Метод половинного ділення. Метод проб у такому вигляді, як описаний вище на ЕОМ не застосовується. Для складання програми і проведення розрахунків на ЕОМ метод проб застосовується у вигляді так званого метода половинного ділення, який в літературі з числових методів можна знайти під назвою "метод дихотомії".

Нехай корінь ξ рівняння , де – неперервна функція, і корінь 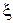відділений на відрізку [а, b], тобто 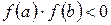, при чому 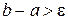. Треба знайти корінь цього рівняння 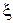з точністю до ε.

Як і раніше, візьмемо на відрізку [а, b] проміжну точку а₁, однак не довільним чином, а так щоб вона знаходилася в середині відрізка, тобто 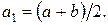Ця точка розділить [а, b] на два відрізки [а, а₁] і [а₁, b], довжина яких дорівнює 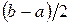(рис. 9). Якщо 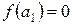, то а₁ буде коренем рівняння . Якщо ж 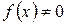, то з двох відрізків [а, а₁] і [а₁, b], що утворилися, вибирають той, на кінцях якого функція приймає значення протилежних знаків. Ітераційний процес продовжують за схемою, розглянутою вище, до тих пір поки не буде знайдено корінь рівняння з заданою точністю, або інакше – поки відрізок [а, b] не стане меншим за ε.

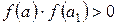Треба відмітити, що функція розраховується з деякою похибкою ε₁. З цих двох відрізків вибираємо той, на кінцях якого функція приймає значення з протилежними знаками. У нашому прикладі і 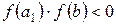, тому вибираємо відрізок [а₁, b].

Процес ділення відрізка навпіл продовжують до тих пір, коли на якомусь n-му етапі або середина буде коренем рівняння (випадок, який рідко зустрічаються на практиці), або буде отриманий відрізок 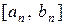такий, що 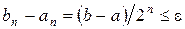і 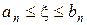(число n вказує на кількість проведених ділень). Числа a_n і b_n – корні рівняння з точністю до ε. За наближене значення кореня треба взяти 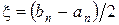, причому похибка не буде перевищувати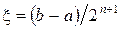

Зазначимо, що при практичній програмній реалізації методу половинного ділення (методу дихотомії) замість розрахунку добутку 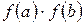, пов’язаного з визначенням однаковості або різниці знаків функції в точках a і b, доцільно скористатися стандартною підпрограмою-функцією SIGN(X) , яка в тому чи іншому вигляді присутня в усіх алгоритмічних мовах. Значення, що видається цією підпрограмою-функцією, відповідає наступному математичному визначенню:

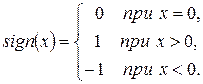
Подібна заміна в алгоритмі методу половинного ділення обґрунтовується тим, що при наближенні точок a і b до кореню рівняння при розрахунку добутку 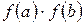може статися зникнення порядку внаслідок малості співмножників. Тому використання знакової функції є переважним.

Оскільки при зменшенні інтервалу в процесі половинного ділення точка а завжди залишається зліва від шуканого кореня, то, не дивлячись на її переміщення, знак 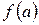не буде змінюватися. Тому знак 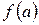визначається тільки один раз, а в процесі ділення вихідного інтервалу узнають знак тільки в середній точці 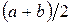і порівнюють його на збіг або розходження зі знаком 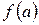. При збігу точку а переміщують в середину відрізка, в протилежному випадку переміщують точку b.

Метод хорд

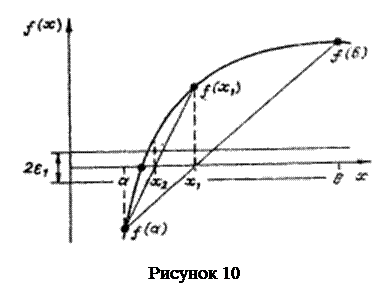
Метод хорд є одним із поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. Він, як і метод половинного ділення, призначений для уточнення кореня рівняння на інтервалі , на кінцях якого ліва частина рівняння 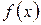приймає різні знаки. На відміну від методу половинного ділення чергове наближення в методі хорд береться не в середині відрізку, а в точці х₁, в якій пряма лінія, проведена через точки 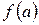і 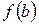, перетинає вісь абсцис (рис. 10). Отже, ідея методу хорд полягає в тому, що на достатньо малому проміжку дуга кривої 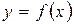замінюється стягуючою її хордою і за наближене значення кореня приймається точка перетину хорди з віссю абсцис.

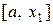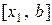За новий інтервал для продовження ітераційного процесу вибирають той з двох або , на кінцях якого функція 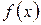приймає значення з різними знаками.

Процес уточнення кореня закінчується, коли відстань між черговими наближеннями буде менше заданої похибки ε₁

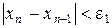
або коли значення функції 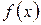попадуть в область шуму, тобто

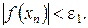
Рівняння прямої лінії, що проходить через точки 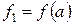і 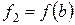має вигляд

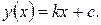
Коефіцієнти k і c рівняння цієї прямої визначають наступним чином

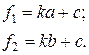
Розв’язавши цю систему рівнянь, отримують

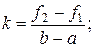
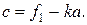
Точку перетину прямої 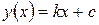з віссю абсцис знаходять, прирівнюючи 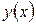до нуля

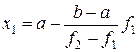
або

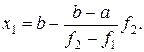
На завершення треба відзначити, що в більшості випадків при розв’язанні рівнянь методом хорд застосовується менша кількість ітерацій порівняно з методом половинного ділення.