Теорема Ролля

Теорема.Пусть функция 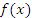дифференцируема в открытом промежутке 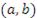, на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения: 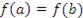. Тогда существует точка 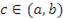, в которой производная функции 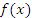равна нулю: .

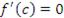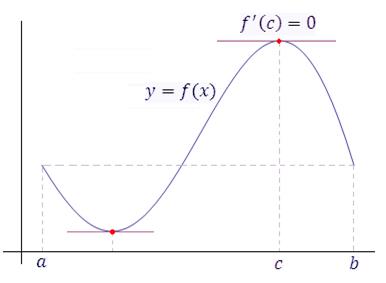
Рис. 3. Теорема Ролляустанавливает условия существования хотя бы одной точки c, в которой касательная к графику функции параллельна оси 0x. Таких точек может быть несколько.

Доказательство. Если 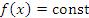в промежутке 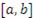, то 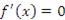во всех точках этого промежутка. Иначе наибольшее значение M функции 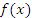превышает ее наименьшее значение m в промежутке 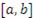. Поскольку на концах этого промежутка функция 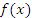принимает одинаковые значения, то по крайней мере одно из значений, M или m, достигается во внутренней точке c промежутка 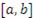. Тогда по теореме Ферма .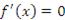