Ряд а) расходится, ряд в) сходится 4 страница
Решение:
Для вычисления определенного интеграла применим формулу Ньютона – Лейбница: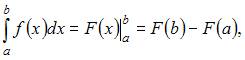 
где 
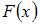– первообразная функции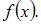 
Тогда
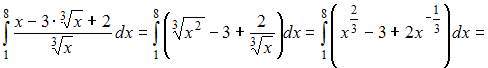
3. Несобственный интеграл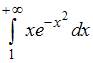 
…
равен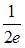 
равен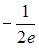 
расходится
равен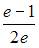 
Решение:
Для вычисления данного несобственного интеграла применим обобщенную формулу Ньютона – Лейбница вида: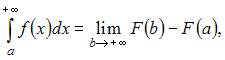 
где 
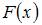– первообразная функции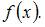 
Вычислим предварительно неопределенный интеграл:
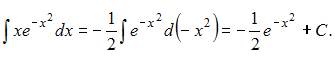
Тогда
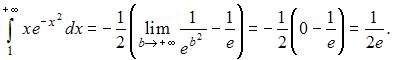
4. Определенный интеграл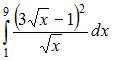 
равен …
– 112
Решение:
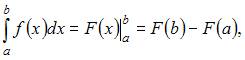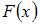Для вычисления определенного интеграла применим формулу Ньютона – Лейбница: где – первообразная функции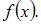
Тогда
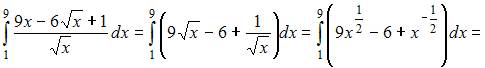
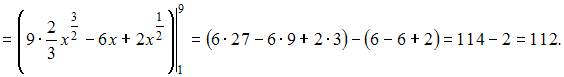
5. Определенный интеграл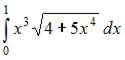 
равен …
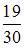- правильно
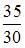
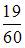
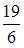
Решение:
Для вычисления данного определенного интеграла произведем замену переменных: 
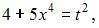
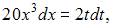
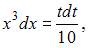и перейдем к новым пределам интегрирования: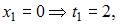 
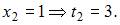
Тогда
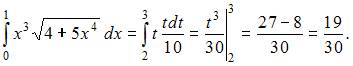
6. Определенный интеграл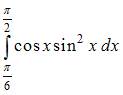 
равен …
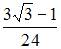- правильно
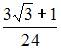
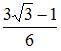
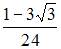
Решение:
Для вычисления данного определенного интеграла произведем замену переменных: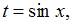 
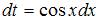и перейдем к новым пределам интегрирования: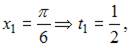 
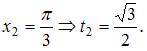
Тогда
Тема 16: Приложения определенного интеграла
1. Объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной параболой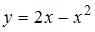 
и осью Ох, равен …
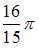- правильно
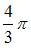
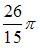
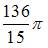
Решение:
Вычислим точки пересечения параболы 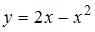с осью Ох, решив уравнение 
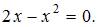Получим точк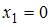и 
и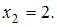 
Тогда объем тела, полученного вращением соответствующей криволинейной трапеции вокруг оси Ох, вычисляется как:
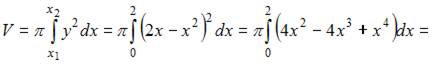
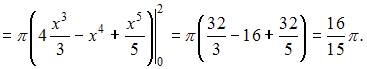
2. Площадь фигуры, изображенной на рисунке,
равна …
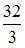- правильно
Решение:
Площадь данной фигуры можно вычислить по формул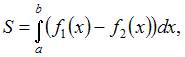е 
где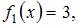 
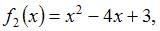
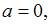
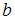– «правая» точка пересечения параболы 
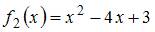и прямой 
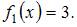Решив уравнение 
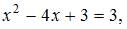определим значение 
получаем 
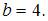Тогда
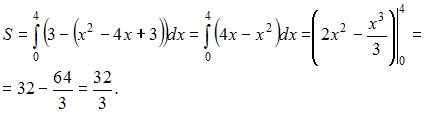
3. Площадь фигуры, ограниченной параболой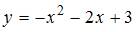 
и осью Ох, равна …
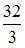- правильно
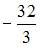
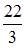
Решение:
Площадь данной фигуры можно вычислить по формуле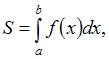 
где 
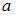и 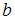– это точки пересечения параболы и оси Ох, а 
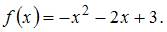Определим точки пересечения параболы и оси Ох, решив уравнение 
получаем 
и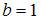 
. Тогда
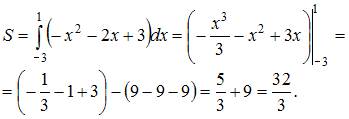
4. Площадь фигуры, изображенной на рисунке,
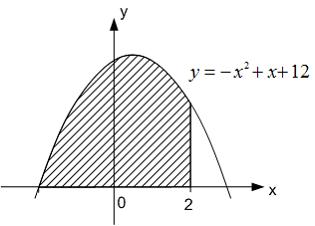
равна …
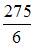- правильно
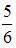
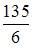
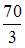
Решение:
Площадь данной фигуры можно вычислить по формул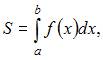е 
где 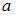– «левая» точка пересечения параболы и оси Ох, 
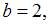а 
Решив уравнение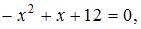 
определим точки пересечения параболы и оси 
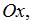получаем 
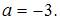Тогда
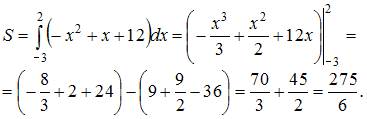
5. Площадь фигуры, ограниченной параболой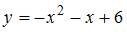 
и осью Ох, равна …
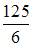- правильно
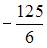
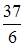
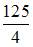
Решение:
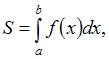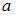Площадь данной фигуры можно вычислить по формуле где и 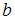– это точки пересечения параболы и оси Ох, а 
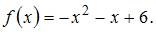Определим точки пересечения параболы и оси Ох, решив уравнение 
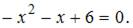Получаем и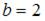 
. Тогда
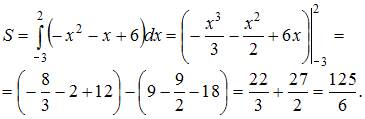
6. Длина дуги кривой 
от точки 
до точки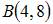 
равна …
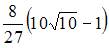- правильно
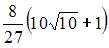
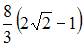
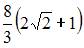
Решение:
Длина дуги плоской кривой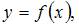 
ограниченной прямыми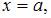 
определяется по формуле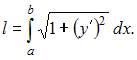 
В нашем случае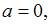 
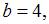а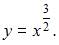 
Тогда
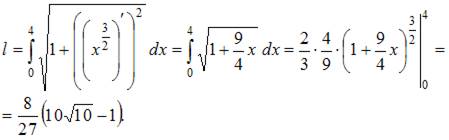
Тема 17: Числовые последовательности
1. Из числовых последовательностей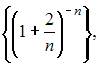 
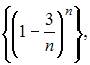
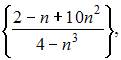
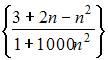бесконечно малой является последовательность …
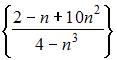- правильно
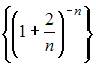
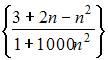
Решение:
Последовательность называется бесконечно малой, если предел ее общего члена при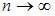 
равен 0.
Для последовательности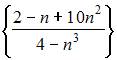 
имеем
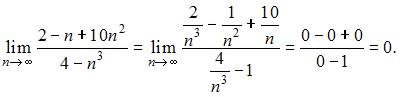
Остальные последовательности не являются бесконечно малыми, в чем легко убедиться, вычислив пределы общего члена.
2. Общий член числовой последовательности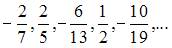 
имеет вид …
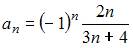- правильно
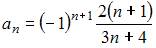
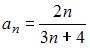
Решение:
Если представить данную последовательность в виде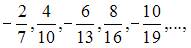 
то легко заметить, что из предложенных ответов правильным является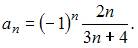 
3. Числовая последовательность задана рекуррентным соотношением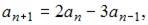 
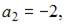
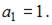Тогда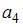 
равно …
– 8
– 20
– 7
4. Предел числовой последовательности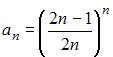 
равен …
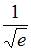- правильно
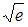
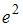
Решение:
Так как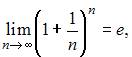 
то 
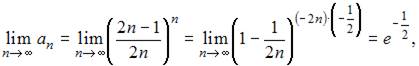или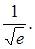 
5. Предел числовой последовательности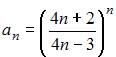 
равен …
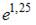- правильно
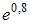
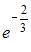
Решение:
Так как 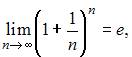то
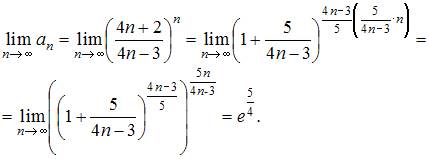
6. Из числовых последовательностей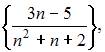 
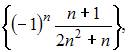
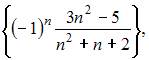
не является сходящейся последовательность …
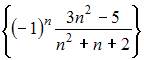- правильно
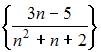
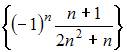
Решение:
Последовательность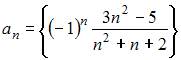 
при четных 
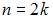примет вид 
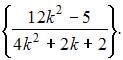Ее предел будет равен
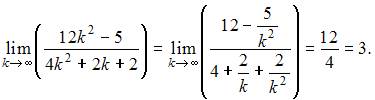
При нечетных 
последовательность примет вид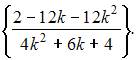 
Ее предел будет равен:
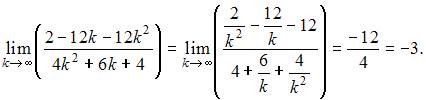
Так как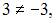 
то данная последовательность не является сходящейся.
Остальные последовательности являются сходящимися, в чем легко убедиться, вычислив пределы общего члена.
7. Предел числовой последовательности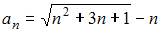 
равен …
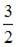- правильно
Решение:
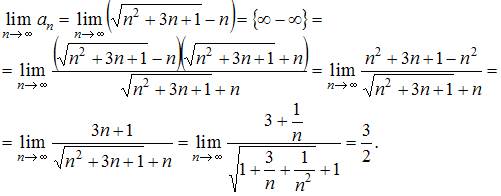
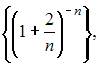
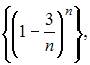
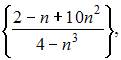
8. Из числовых последовательностей 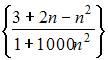бесконечно малой является последовательность …
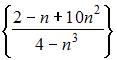- правильно
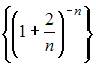
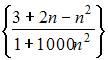
Тема 18: Сходимость числовых рядов
1. Даны числовые ряды:
А)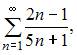 
В)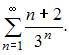 
Тогда верным является утверждение …
ряд А) расходится, ряд В) сходится
ряд А) расходится, ряд В) расходится
ряд А) сходится, ряд В) сходится
ряд А) сходится, ряд В) расходится
Решение:
Ряд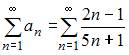 
расходится, так как для него не выполняется необходимое условие сходимости. Действительно,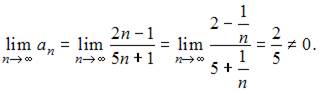 
Для исследования сходимости ряда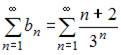 
применим признак сходимости Даламбера. Тогда 
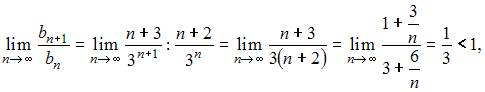то есть ряд сходится.
2. Даны числовые ряды:
А)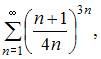 
В)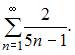 
Тогда верным является утверждение …