Вычисление пределов функции
· Непосредственное вычисление состоит в том, что вместо аргумента x подставляется его предельное значение, и выполняются все необходимые операции.
· Раскрытие неопределенности вида 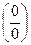 состоит в сокращении дроби на множитель, стремящийся к нулю, при этом, если:
состоит в сокращении дроби на множитель, стремящийся к нулю, при этом, если:
§ в числителе и знаменателе дроби многочлены, то их следует разложить на линейные множители 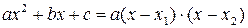 или, если квадратное уравнение приведенное
или, если квадратное уравнение приведенное 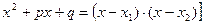
§ под знаком предела иррациональное выражение (выражение, содержащее корень ), то следует числитель и знаменатель умножить на сопряженный множитель [например, для получения формулы (a–b)(a+b)= a2–b2].
§ под знаком предела находится тригонометрическое выражение, то следует его преобразовать так, чтобы дробь сократилась.
Задача 1.Вычислить предел: 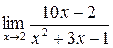
Решение: подставим в дробь, стоящую под знаком предела, x=2:
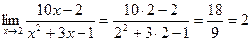
Задача 2. Вычислить предел: 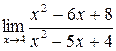
Решение: при непосредственной подстановке x=4 в дробь, получаем неопределенность вида 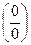 . Разложим квадратные трехчлены в числителе и в знаменателе на множители.
. Разложим квадратные трехчлены в числителе и в знаменателе на множители.
x2-6x + 8 = 0 По т. Виета 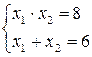 Þ x1=4, x2=2 Þ x1=4, x2=2 | x2-5x + 4 = 0 По т. Виета 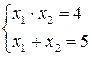 Þ x1=1, x2=4 Þ x1=1, x2=4 |
Тогда: 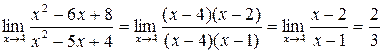 .
.
Задача 3. Найти следующие пределы:
3.1. a) 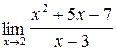 ;б)
;б) 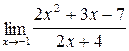 ;
;
3.2. a) 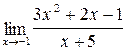 ;б)
;б) 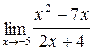 ;
;
3.3. a) 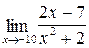 ;б)
;б) 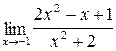 ;
;
3.4. a) 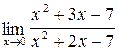 ;б)
;б) 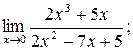
3.5. a) 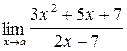 ;б)
;б) 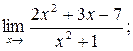
3.6. a) 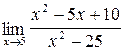 ;б)
;б) 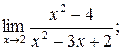
3.7. a) 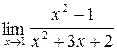 ;б)
;б) 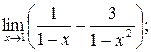
3.8. a) 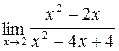 ;б)
;б) 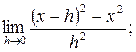
3.9. a) 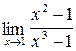 ;б)
;б) 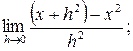
3.10. a) 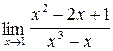 ;б)
;б) 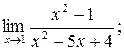
Практическое занятие №4
Первый замечательный предел
Предел вида 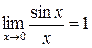 называется первым замечательным пределом.
называется первым замечательным пределом.
Следствия:
1. 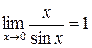 , 2.
, 2. 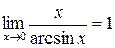 , 3.
, 3. 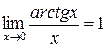 ,
,
4. 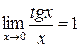 , 5.
, 5. 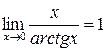 , 6.
, 6. 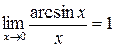 ,
,
7. 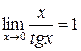 .
.
Задача 1. Вычислить предел: 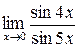
Решение:При непосредственной подстановке имеем неопределенность вида 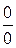 . Преобразуем дробь, стоящую под знаком предела так, чтобы задача была сведена к первому замечательному пределу:
. Преобразуем дробь, стоящую под знаком предела так, чтобы задача была сведена к первому замечательному пределу:
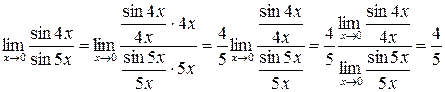
[т.к. и числитель, и знаменатель полученной дроби представляет собой первый замечательный предел].
Задача 2.
2.1. a) 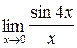 ;б)
;б) 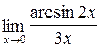 ;
;
2.2. a) 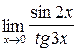 ;б)
;б) 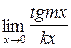 ;
;
2.3. a) 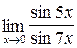 ;б)
;б) 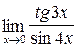 ;
;
2.4. a) 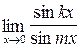 ;б)
;б) 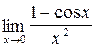 ;
;
2.5. a) 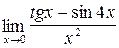 ;б)
;б) 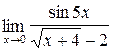 ;
;
2.6. a) 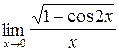 ;б)
;б) 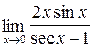 ;
;
2.7. a) 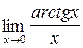 ;б)
;б) 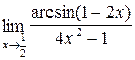 ;
;
2.8. a) 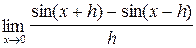 ;б)
;б) 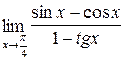 ;
;
2.9. a) 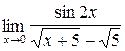 ;б)
;б) 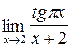 ;
;
2.10. a) 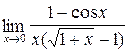 ;б)
;б) 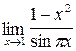 ;
;
2.11. a) 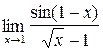 ;б)
;б) 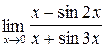 ;
;
Практическое занятие № 5,6
Непрерывность функции в точке. Локальные свойства непрерывной функции. Точки разрыва. Глобальные свойства непрерывных функций
Непрерывность в точке
Определение 1. Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 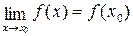
Определение 2. функция y=f(x) называется непрерывной в точке х0, если она определена в точке х0 и ее окрестности и выполняется равенство 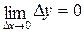 , где
, где 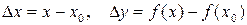 , т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Задача 1. Исследовать на непрерывность функцию y=sin x.
Решение. Функция y=sin x определена при любом х. Возьмем произвольную точку х и найдем приращение Dу:
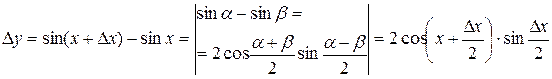 .
.
Тогда 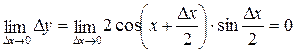 , т.к. произведение ограниченной функции и бесконечно малой функции (б.м.ф.) есть б.м.ф.
, т.к. произведение ограниченной функции и бесконечно малой функции (б.м.ф.) есть б.м.ф.
2. Непрерывность функции в интервале и на отрезке.
Определение 3. Функция y=f(x) называется непрерывной в интервале (a,b), если она непрерывна в каждой точке этого интервала.
Определение 4. Функция y=f(x) называется непрерывной на отрезке [a;b], если она непрерывна в интервале (a,b) и в каждой точке х=a непрерывна справа (т.е. 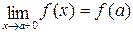 ), а в точке х=b непрерывна слева (т.е.
), а в точке х=b непрерывна слева (т.е. 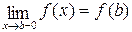 ).
).
3. Точки разрыва функции и их классификация.
Определение 5. Точки в которых нарушается непрерывность функции называются точками разрыва этой функции.
х=х0 – точка разрыва если не выполняется по крайней мере одно из условий определения 1, а именно:
1. функция определена в окрестности точки х0, но не определена в самой точке. (например, 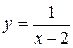 ).
).
2. функция определена в точке х0 и ее окрестности, но не существует предела f(x) при х®х0.
Задача 2. Задана функция у=f(x). Найти точки разрыва, если они существуют. 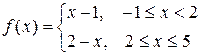 .
.
Решение. Функция определена в точке х=2 (f(2)=0), однако в точке х=2 имеет разрыв, так как односторонние пределы при х®2 слева и справа не равны между собой:
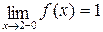 ,
, 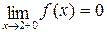 .
.
3. функция определена в точке х0 и ее окрестности, существует 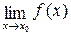 но этот предел не равен значению функции в точке х0:
но этот предел не равен значению функции в точке х0: 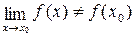 .
.
Задача 3. Задана функция у=f(x). Найти точки разрыва, если они существуют. 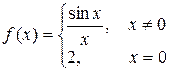 .
.
Решение: Здесь х0=0 – точка разрыва: предел функции неравен значению функции в этой точке 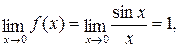 однако
однако 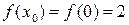 .
.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение 6. Точка х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. 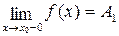
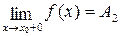 . При этом:
. При этом:
а) если А1=А2, то точка х0 называется точкой устранимого разрыва;
б) если А1¹А2, то точка х0 называется точкой конечного разрыва.
Величину ½А1–А2½ называют скачком функции в точке разрыва первого рода.
Определение 7. Точка называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
Задача 4. Задана функция у=f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа;
3) сделать схематический чертеж.
4.1. f(x)=52/(2–x) x1=0 x2=2 4.2. 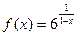 x1=0 x2=1
x1=0 x2=1
4.3. f(x)=111/x x1=0 x2=4 4.4. f(x)=31/(7–x) x1=1 x2=7
4.5. f(x)=42/(1+x) x1=0 x2= –1 4.6. 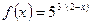 x1=1 x2=2
x1=1 x2=2
4.7. 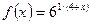 x1=0 x2= –4 4.8.
x1=0 x2= –4 4.8. 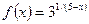 x1=1 x2=5
x1=1 x2=5
4.9. 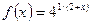 x1=1 x2= –2 4.10.
x1=1 x2= –2 4.10. 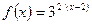 x1=3 x2=2
x1=3 x2=2
Задача 5. Задана функция у=f(x). Найти точки разрыва, если они существуют. Сделать чертеж.
5.1. f 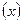 =
= 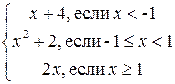 . 5.2.
. 5.2. 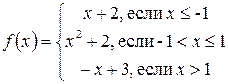 .
.
5.3. f 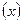
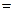
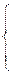
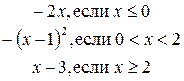 .
.  5.4. f
5.4. f 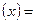
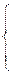
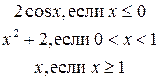 .
.
5.5. f 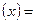
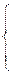
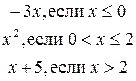 . 5.6. f(x) =
. 5.6. f(x) = 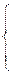
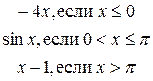 .
.
5.7. f(x) = 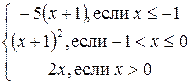 . 5.8. f(x) =
. 5.8. f(x) = 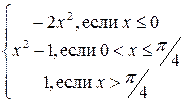 .
.
5.9. 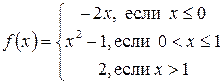 . 5.10. f
. 5.10. f 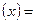
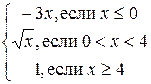 .
.
Практическое занятие №7
