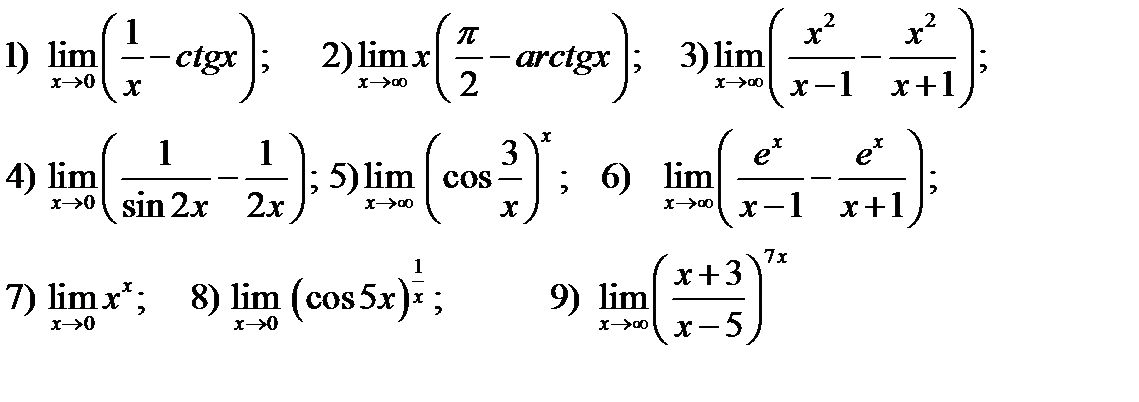Теорема о среднем в дифференцировании (Лагранжа). Первое и второе правила Лопиталя. Вычисление пределов с помощью правила Лопиталя

Глава 4.

Тема 5 .

Напомним определения локальных экстремумов функций.

Определение 5.1. Функция 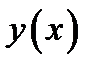имеет локальный максимум в точке 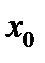, если существует окрестность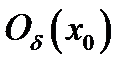 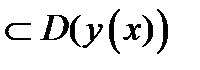, в которой 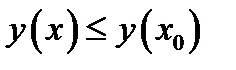для всех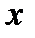 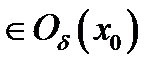. Точка 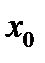называется точкой локального максимума. Значение функции в этой точке называется значением локального максимума.

Определение 5.2.Функция 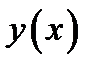имеет локальный минимум в точке 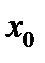, если существует окрестность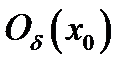 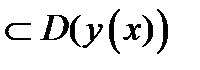, в которой 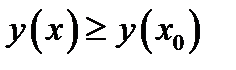для всех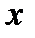 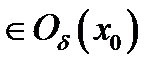. Точка 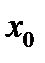называется точкой локального минимума. Значение функции в этой точке называется значением локального минимума.

Определение 5.3.Точками локальных экстремумов назовём точки локальных минимумов либо локальных максимумов. Значение локального максимума или минимума назовём значением локального экстремума.

Определение критической точки функции. Пусть функция 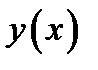задана на интервале 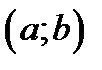. Точка 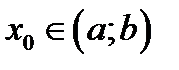называется критической точкой функции 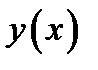тогда и только тогда, когда выполнены условия: а) производная функции 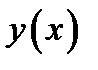существует и 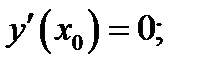или в) 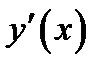не существует.

Теорема Ферма. Если функция 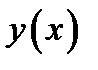имеет в точке 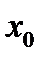локальный экстремум, то эта точка 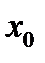является критической точкой.

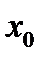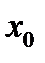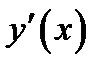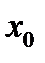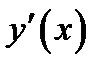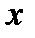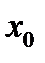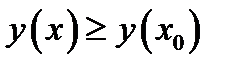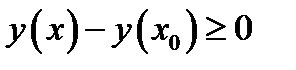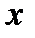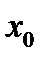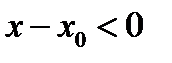Доказательство. Пусть точка экстремальная. Если в точке производная не существует, то по определению она критическая. Если в точке производная существует, то докажем, что в этом случае она равна нулю. Для простоты рассмотрим случай, когда экстремальная точка является точкой локального минимума. То есть если лежит вблизи , то и . Если точка лежит слева от точки , то и

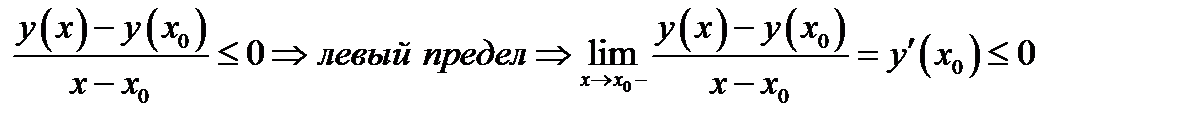
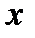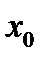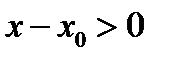Если точка лежит справа от точки , то и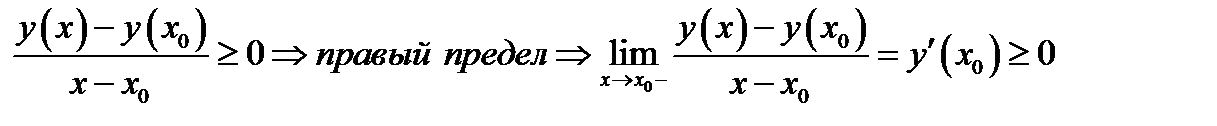

Так как по предположению производная существует, то левый предел должен быть равен правому пределу. А это возможно когда 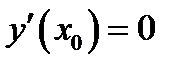. Аналогично рассматривается случай, когда точка 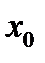является точкой локального максимума.

Теорема Ролля.Если функция 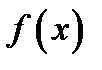непрерывна на отрезке 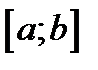, дифференцируема в интервале 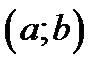и на концах отрезка 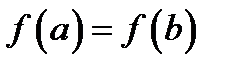, то найдётся точка 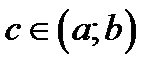в которой .

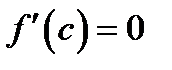Доказательство. По свойству непрерывных на отрезке функций существуют точки минимума и максимума 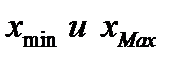. Если 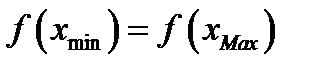, то 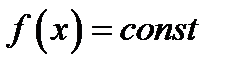для всех 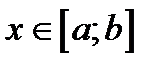. В этом случае для любой точки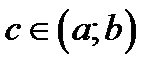 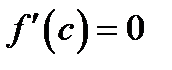. Если 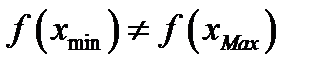,то либо 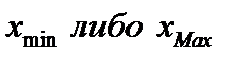лежит внутри интервала 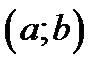. Обозначив эту точку буквой получим 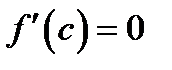по теореме Ферма.

Теорема о среднем в дифференцировании (Лагранжа).

Пусть функция 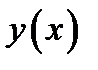непрерывна в замкнутом интервале 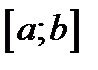и имеет производную в каждой точке 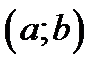. Тогда найдётся, точка из интервала 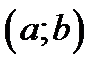такая, что

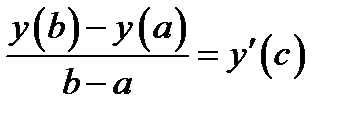(5.1)

или

B

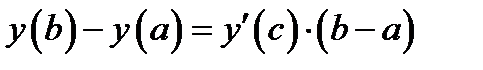(5.2)

C

A

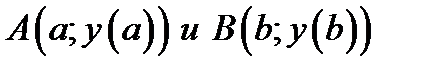Геометрический смысл теоремы о среднем простой. Дробное отношение в левой части равенства (5.1) это тангенс угла наклона секущей прямой проходящей через конечные точки графика . Производная в точке 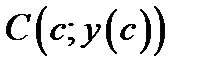в правой части (5.1) это тангенс угла наклона касательной прямой. Теорема говорит о том, что для секущей прямой проходящей через конечные точки графика всегда найдётся параллельная ей касательная к графику (рис.1).

рис.1

Доказательство. Рассмотрим вспомогательную функцию

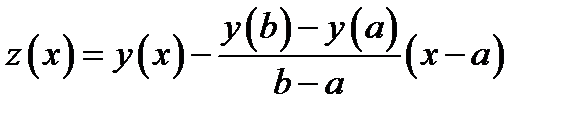(5.3)

Проверим, что для этой функции выполнены все условия теоремы Ролля. Действительно эта функция непрерывна на отрезке 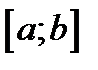и и имеет производную в каждой точке 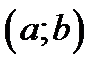. Кроме того

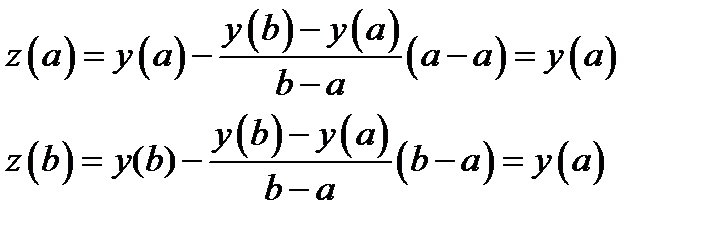
Следовательно, существует точка 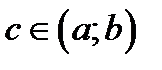в которой 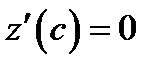. Отсюда

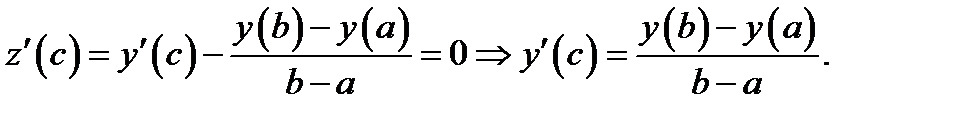
И теорема Лагранжа о среднем в дифференцировании доказана.

Рассмотрим полезное обобщение теоремы о среднем в дифференцировании .

Теорема Коши. Пусть 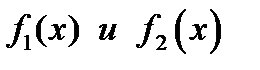- непрерывные на отрезке 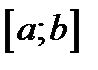функции, у которых производные 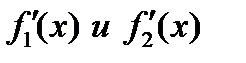определены и непрерывны на 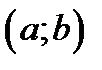, причём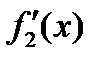 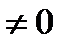. Тогда существует число 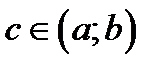такое, что справедлива формула

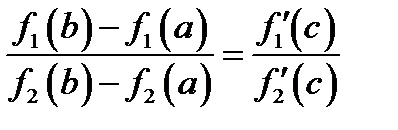(5.4)

Замечание. Если в теореме Коши взять 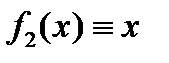, то мы получим теорему Лагранжа. Поэтому, теорема Коши является обобщением теоремы Лагранжа.

Доказательство. Доказывать будем по схеме доказательства теоремы Лагранжа.

Рассмотрим вспомогательную функцию .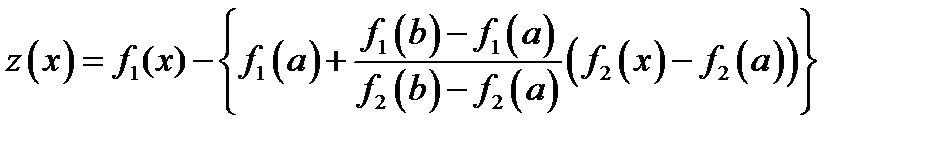

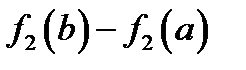
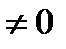, так как по условию 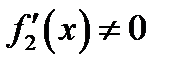. Проверкой убеждаемся, что 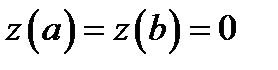. Производная функции 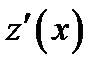на интервале 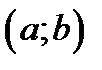равна

.

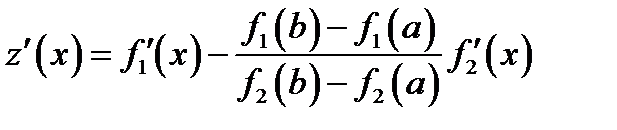По теореме Ролля существует точка 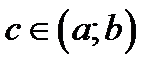, что

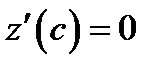
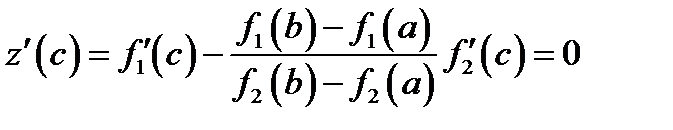или .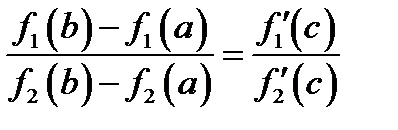

Теорема Коши доказана.

Полезное следствие. Если 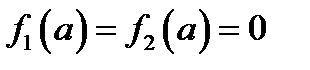, то для любых 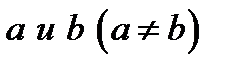существует число 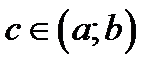, что

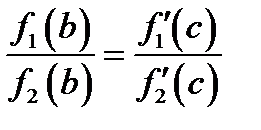(5.5)

Используя полученную формулу (5.5), докажем правило вычисления некоторых пределов, называемым правилом Лопиталя.

Первое правило Лопиталя. Если 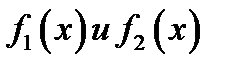удовлетворяют условиям теоремы Коши и

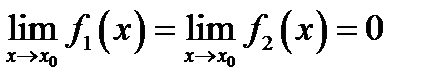(5.6)

Существует предельное значение ,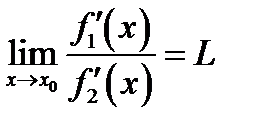

тогда

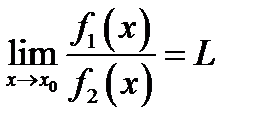(5.7) Доказательство. Докажем теорему для случая когда 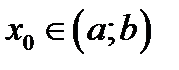конечное число. Пусть выполнено условие теоремы (5.6). Так как функции 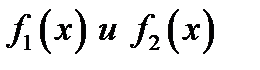непрерывны, то 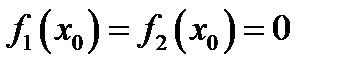и на любом из отрезков 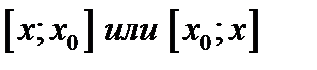лежащем в 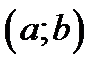выполнены условия теоремы Коши.

По формуле (5.4) всегда найдётся между 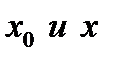такое, что

.

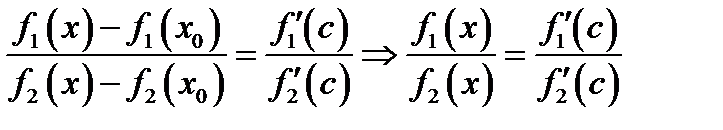Отсюда следует, если 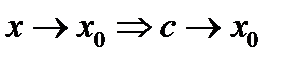и поэтому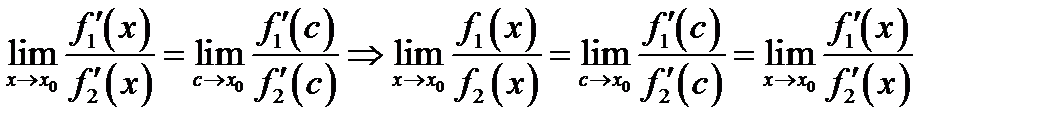

Следовательно 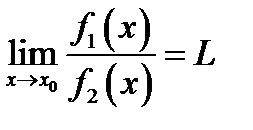. И первое правило Лопиталя доказано.

Пример 5.1.Вычислить пределы1) 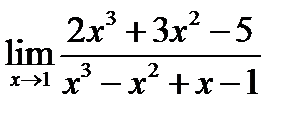; 2) .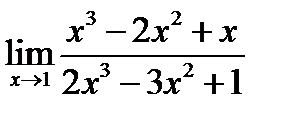

Вычисляем первый предел .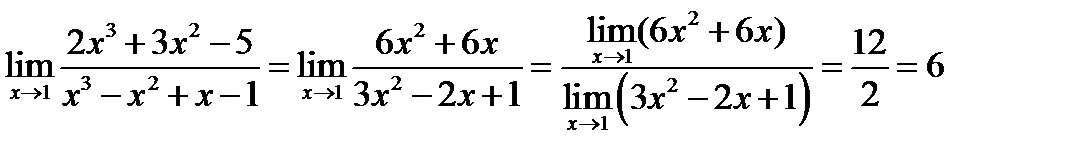

Вычисляем второй предел

.

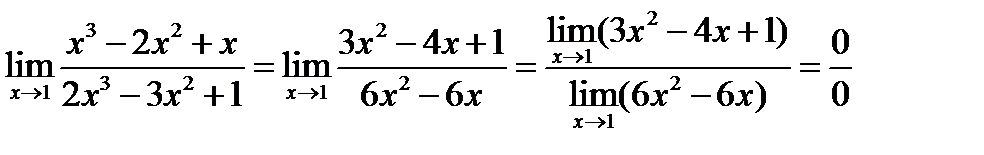Применяем правило Лопиталя повторно

.

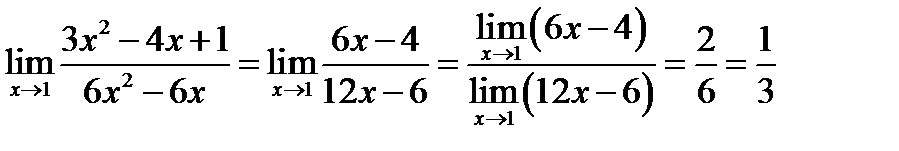Краткая запись будет выглядеть так

=

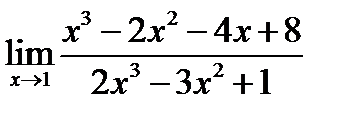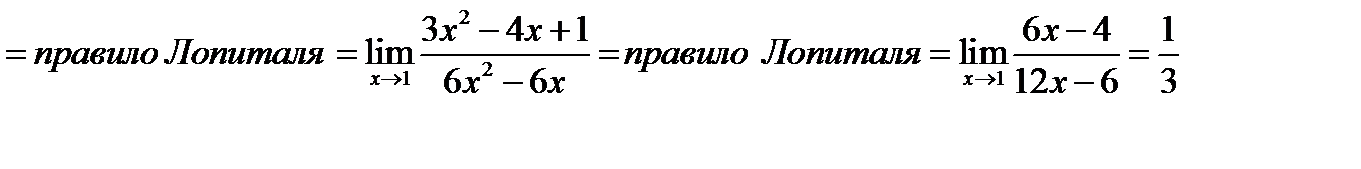
Второе правило Лопиталя. Если 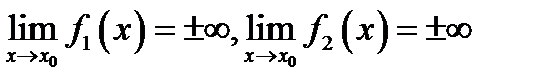и предельное значение

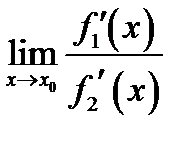существует, то

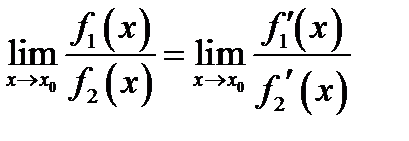(5.8)

Примем это правило без доказательства. Доказательство можно найти в любом курсе математического анализа.

Замечание.Правила Лопиталя остаются справедливыми, если .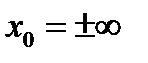

Замечание. При пользовании правилом Лопиталя, не путайте правильное выражение 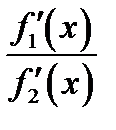с неправильным 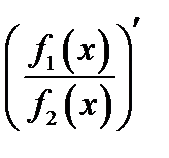выражением.

Пример 5.2. Используя второе правило Лопиталя вычислить пределы

Решение. 1) Вычисляем предварительно .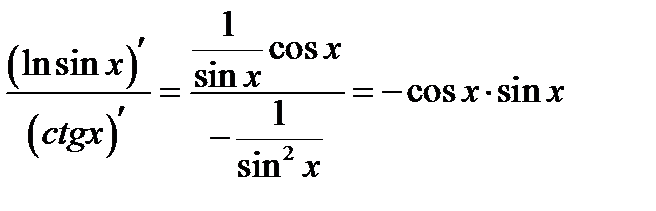

Тогда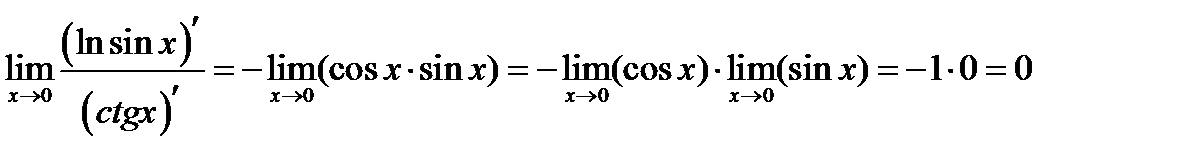

Тогда по правилу (5.8)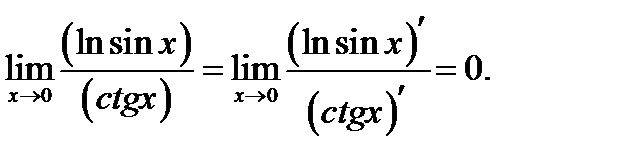

2) Вычисляем предварительно 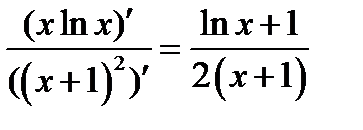. Применяем правило

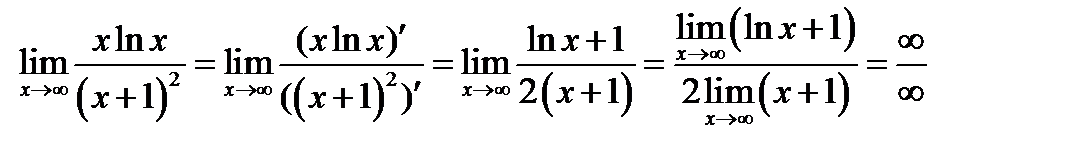
Результат показывает, что правило нужно применять повторно

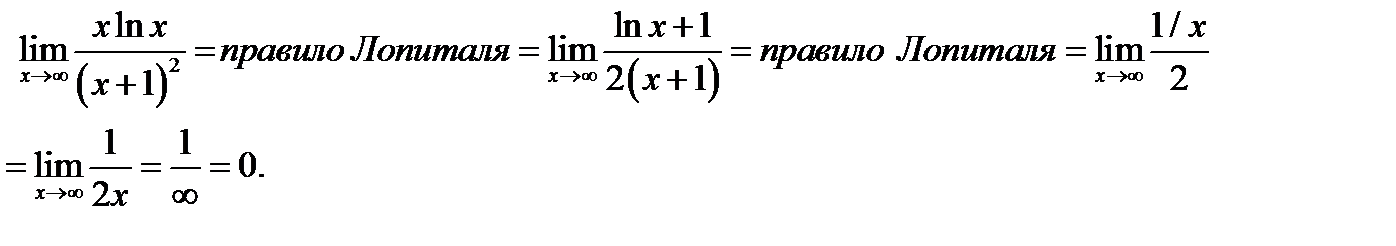
Пример 5.3. Докажем формулу второго замечательного предела 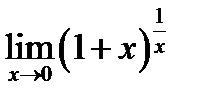. Положим 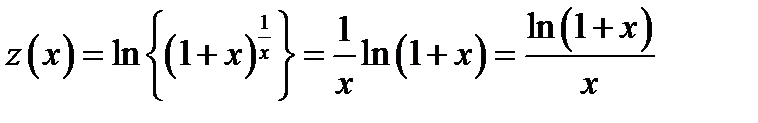. Вычислим предел функции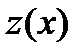

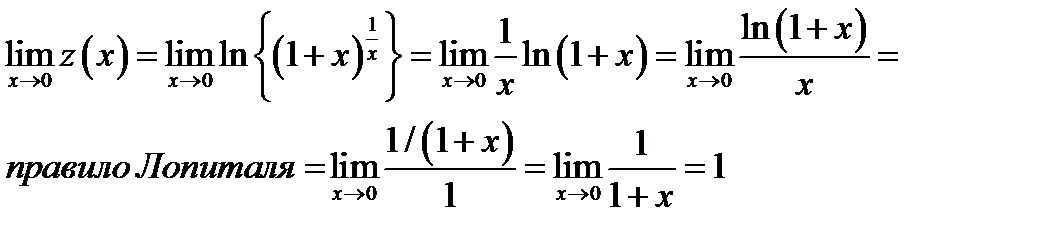
Таким образом 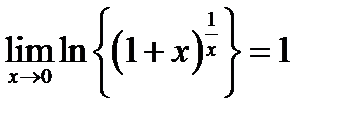. Так как логарифмическая функция непрерывна, то

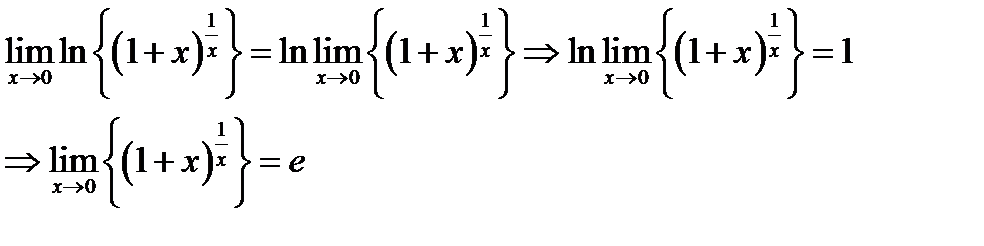
Другие случаи применения правила Лопиталя.Правила Лопиталя позволяют вычислять не только пределы дробей типа 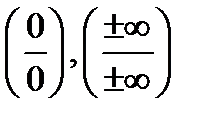, но также пределы и других типов. Рассмотрим различные случаи.

1 случай 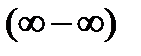. Найти предел .

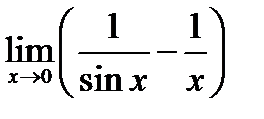Решение. Вычисление данного предела сводим к использованию правила Лопиталя.

Для этого преобразуем выражение к общему знаменателю

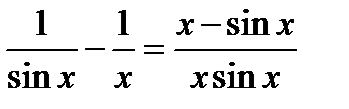. Переходя к пределу, получим =

= .

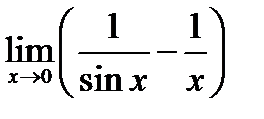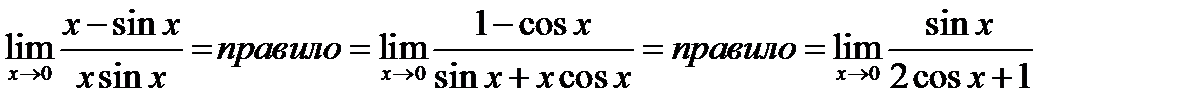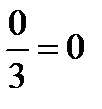2 случай ( 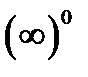). Найти пределы 1) 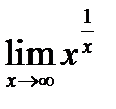; 2)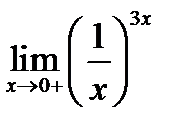

Решение. 1) Вычисление данного предела сводим к использованию правила Лопиталя.

Для этого преобразуем данное выражение к дроби с помощью операции логарифмирования степени. Обозначим .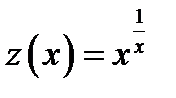

Тогда 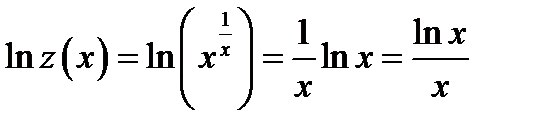. Вычисляем предел полученного выражения

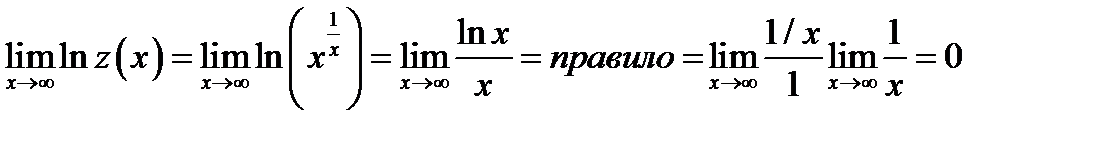. Итак .

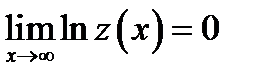Так как логарифмическая функция непрерывна, то

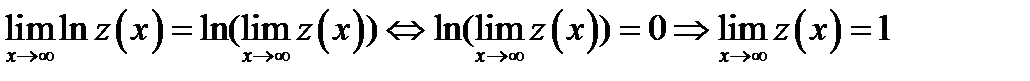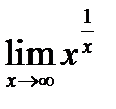или =1.

2) Преобразуем данное выражение к дроби с помощью операции логарифмирования

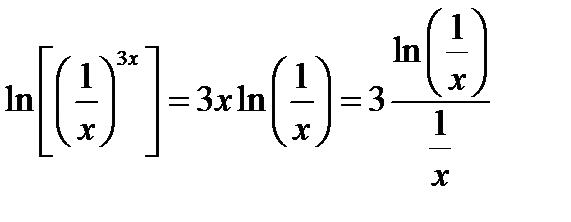; Переходя к пределу пользуемся правилом Лопиталя

;

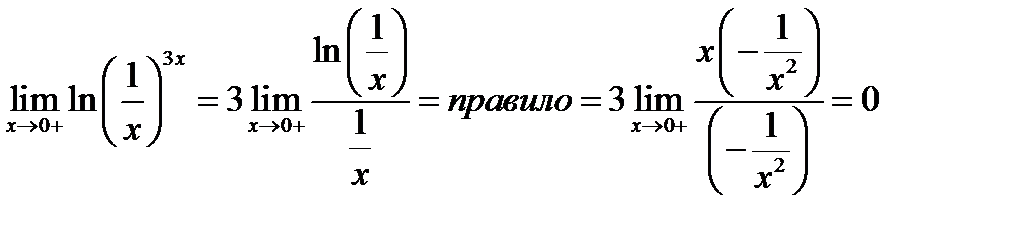Обозначим 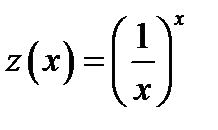. Так как логарифмическая функция непрерывна, то

0= 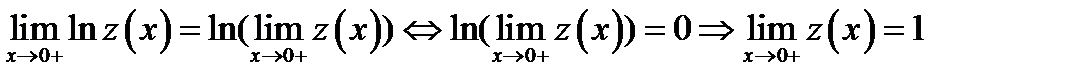. Или .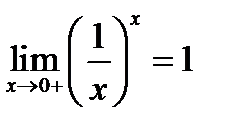

3 случай 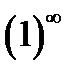. Найти пределы 1)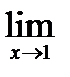 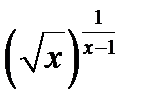; 2)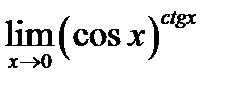

Вычисление данного предела сводим к использованию правила Лопиталя. Для этого преобразуем данное выражение к дроби с помощью операции логарифмирования Обозначим 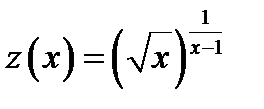. Тогда 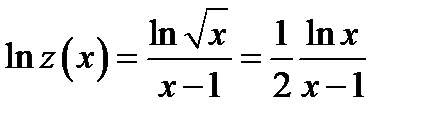. Вычисляем предел полученного выражения 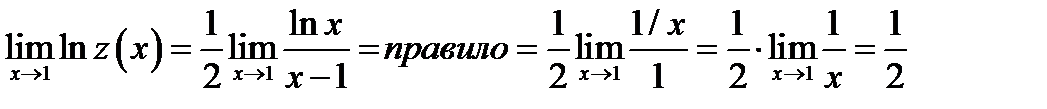. По аналогии с предыдущими примерами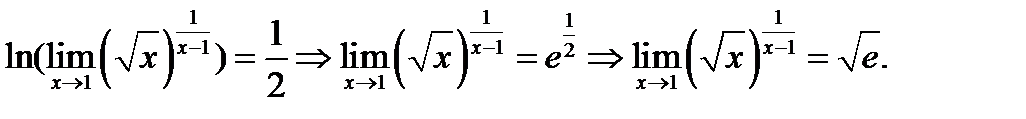

2) Преобразуем данное выражение к дроби с помощью операции логарифмирования

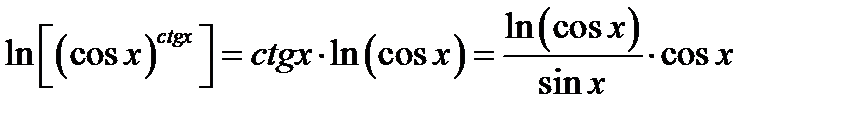. Вычисляем предел полученного выражения

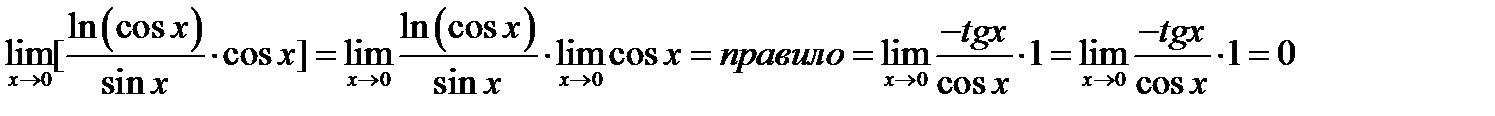
Обозначим 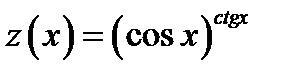. Так как логарифмическая функция непрерывна, то

0= 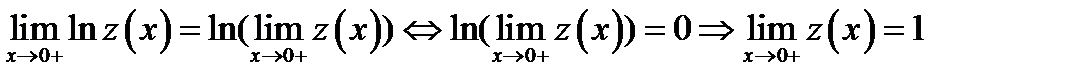. Или .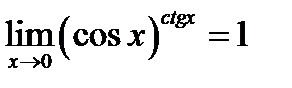

Контрольные вопросы.

I.Дайте геометрические иллюстрации теорем: Ферма, Ролля, Лагранжа.

II.Какая теорема используется для доказательства правила Лопиталя.

III.Почему нельзя использовать теорему Лагранжа для доказательства правила Лопиталя.

IV.Сформулируйте первое правило Лопиталя.

V.Сформулируйте второе правило Лопиталя.

Далее предлагаются упражнения по данной теме для самостоятельной работы . В разделе ответы и решения приведены решения упражнений и ответы.

Упражнение 5.1 . Вычислить указанные пределы

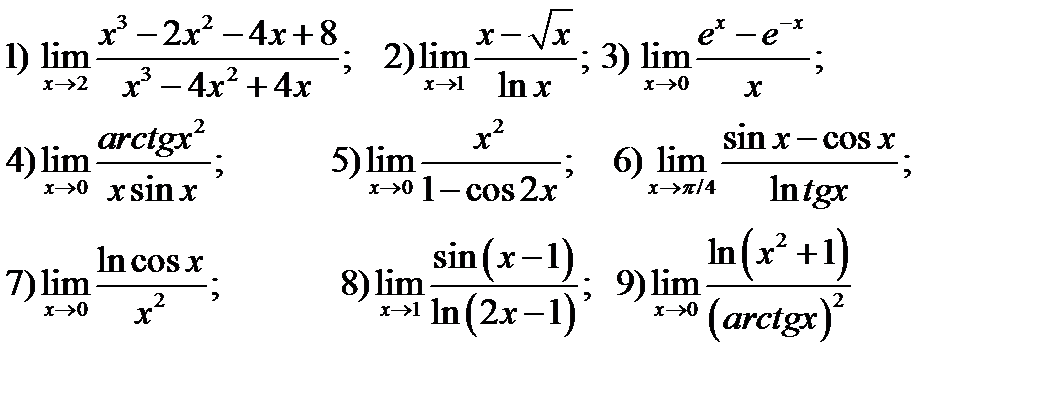
Упражнение 5. 2. Вычислить указанные пределы