Аналітичний метод доведення нерівностей

Іноді може виявитися, що застосування розглянутих вище прийомів не приводить до потрібного результату, оскільки доведення нерівності за означенням може не бути реалізованим через громіздкість та складність перетворень, а синтетичний метод не вдається застосувати у зв’язку з тим, що не зрозуміло, з яких опорних нерівностей доцільно розпочати доведення. Одним з можливих варіантів у цьому випадку може бути застосування аналітичного методу.

Його суть полягає в тому, що після ряду перетворень нерівності, яку потрібно довести, отримують деяку очевидну вірну нерівність. На мові логіки ми реалізовуємо наступну схему такого пошуку:

,

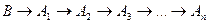де 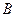- нерівність, яку потрібно довести, 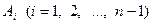- отримані з неї нерівності, 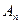- кінцева вірна нерівність. Реалізація такої схеми носить назву аналізу Евкліда. Природно, що відшукання нерівності 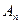не може завершити доведення, оскільки імплікація 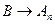може бути вірною і у випадку, коли твердження 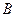- хибне. Тому наступним етапом доведення повинно бути обґрунтування можливості здійснення зворотних міркувань, тобто істинності імплікацій

.

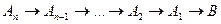Фактично тепер ми реалізовуємо схему синтетичного методу, причому початкова опорна нерівність цього методу (у нашому випадку – це твердження 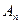) відома.

Наведемо приклади подібних доведень.

Задача 1.3.1. Довести, що для довільних 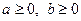виконується нерівність

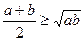
(задача 1.1.1, розв’язання якого тут реалізується іншим методом).

Доведення. Виконаємо наступні перетворення даної нерівності:

,

,

.

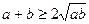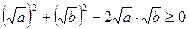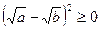Одержана нерівність вірна для довільних 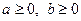. Тепер очевидно, що з неї можна одержати попередню нерівність, з якої в свою чергу – нерівність, що потрібно було довести.

Задача 1.3.2. Довести, що для довільних чисел 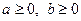виконується нерівність

.

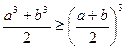Доведення. Очевидно, що якщо 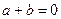, то виконується рівність і твердження вірне. При 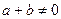задача зводиться до доведення нерівності 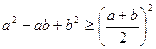або нерівності 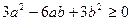, яка очевидна.

Інший спосіб доведення цієї нерівності, що використовує ідеї опуклості функції, буде наведено у розділі 2.5 (задача 2.5.2).

Задача 1.3.3. Довести, що для довільних 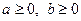виконується нерівність .

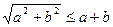Доведення. Після піднесення до квадрату обох частин нерівності, маємо

.

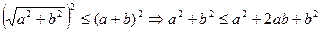Отримуємо вірну нерівність 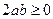. Очевидно, що крім неї, вірними будуть і кожна з попередніх нерівностей.

Задача 1.3.4. Довести, що для довільних 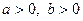виконується нерівність

.

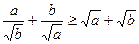Доведення. Піднесемо обидві частини нерівності до квадрату

.

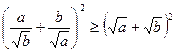Звідси отримуємо

.

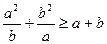
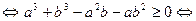
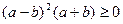Одержана нерівність відповідно до умови задачі вірна, і з неї тепер можна отримати всі попередні нерівності у зворотному порядку, а серед них – і задану.

Задача 1.3.5. Довести, що якщ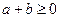о , то .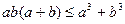

Доведення. Знайдемо різницю правої та лівої частин:

.

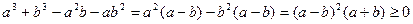Тепер, використавши отриману нерівність в ролі початкової і рухаючись у зворотному порядку, отримуємо нерівність, яку потрібно було довести.

Задача 1.3.6. При яких значеннях параметра 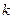нерівність

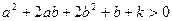
виконується при довільних ?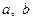

Розв’язання. Маємо

.

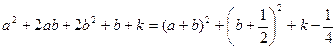Одержаний вираз буде додатним при довільних 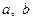, якщо .

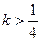Задача 1.3.7. Довести, що при 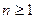виконується нерівність

.

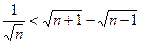Доведення. Перетворимо нерівність до виду 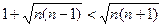, звідки, після піднесення до квадрату, отримуємо

.

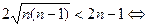
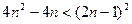Очевидно, що одержана нерівність вірна, а також те, що можливе виконання перетворень у зворотному порядку. Це доводить задану нерівність.

Задача 1.3.8. Знайти найменше значення виразу .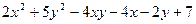

Розв’язання. Перетворимо заданий вираз наступним чином:

.

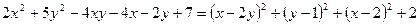Тепер видно, що найменше значення виразу дорівнює 2 і досягається воно при 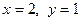.Фактично ми довели нерівність .

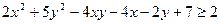Задача 1.3.9.Довести нерівність .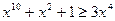

Доведення. Виконаємо наступні перетворення виразу:

.

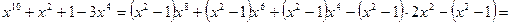
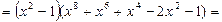
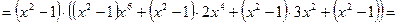
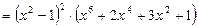Одержаний вираз не може бути від’ємним, що доводить задану нерівність. Очевидно, що знак рівності буде тільки у випадку, коли .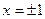

Задача 1.3.10. Знайти найменше значення функції

.

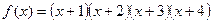Розв’язання. Перетворимо вираз, перемножуючи два крайні та два середні множники:

.

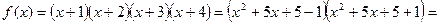
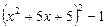Очевидно, що значення функції буде найменшим, коли найменшим є перший доданок, тобто при тих значеннях 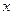, які є коренями рівняння 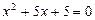. Знаходимо 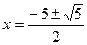. При знайдених значеннях

.
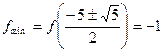