Доведення нерівностей методом математичної індукції

Метод математичної індукції ґрунтується на принципі математичної індукції, що формулюється так: деяке твердження 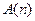істинне для будь-якого натурального 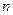, якщо:

1) воно істинне для ;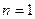

2) з того, що 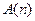істинне для довільного натурального 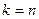випливає, що воно істинне для наступного натурального числа .

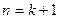Сформульований принцип належить до аксіом натуральних чисел.

Кожне доведення методом математичної індукції передбачає реалізацію трьох етапів: на першому показуємо, що істинним є твердження 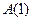; на другому припускаємо, що істинним є твердження 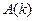і, виходячи з цього, доводимо, що істинним є твердження 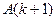. Виконані міркування дозволяють стверджувати, що твердження 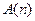істинне для будь-якого натурального 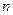. Відповідний висновок є третім етапом і завершує доведення.

Іноді використовують узагальнений принцип математичної індукції: твердження 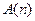істинне для будь-якого натурального 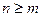, якщо воно вірне для натурального числа 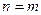і з того, що 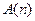істинне для довільного натурального 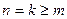випливає, що воно істинне для наступного натурального числа .

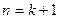Описаний метод широко використовується при обґрунтуванні різних математичних тверджень, зокрема при доведенні нерівностей. Розглянемо це на прикладах.

Задача 1.6.1. Довести, що для довільних 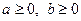та натурального числа 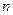виконується нерівність

.

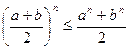Доведення. Очевидно, що при 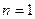виконується рівність, тому дане твердження вірне. Нехай воно істинне при деякому натуральному числі 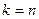, тобто вірно, що 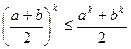. Користуючись цим припущенням, покажемо, що вірною є також нерівність 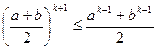. Оскільки ліва частина, згідно з припущенням, обмежена виразом

,

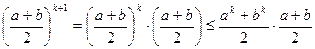то для доведення достатньо показати, що 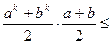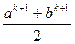. Для цього розглянемо різницю

.

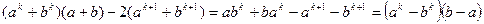Одержаний вираз при 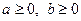завжди від’ємний або дорівнює 0 (при 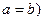, тому 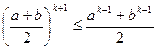. Згідно з принципом математичної індукції вірною є також початкова нерівність .

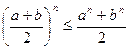Задача 1.6.2. Довести, що для довільного натурального числа 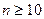виконується нерівність

.

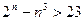Доведення. При 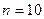отримуємо нерівність 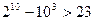, яка вірна. Нехай вона вірна при деякому натуральному числі 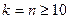, тобто виконується нерівність 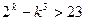. Користуючись цим припущенням, покажемо, що вірною є також нерівність 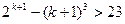. Дістаємо

.

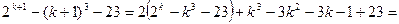
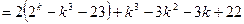Перший доданок одержаного виразу додатний за індуктивним припущенням. Оцінимо суму інших доданків, тобто вираз 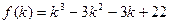. Функція 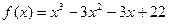має похідну 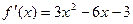та екстремуми у точках 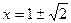, і, очевидно, зростає на проміжку 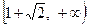. Переконавшись, що 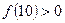, можемо стверджувати, що при 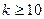виконується нерівність 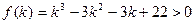. Посилання на принцип математичної індукції завершує доведення.

Задача 1.6.3. Довести, що 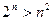для всіх натуральних .

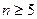Розв’язання. При 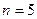отримуємо нерівність 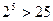, яка вірна. Нехай вона вірна при деякому натуральному числі 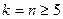, тобто виконується нерівність 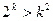. Користуючись цим припущенням, покажемо, що вірною є також нерівність 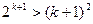. Маємо

,

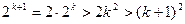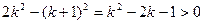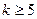оскільки при . На основі принципу математичної індукції стверджуємо, що задана в умові нерівність вірна.

Задача 1.6.4. Довести, що для довільного натурального числа 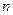виконується нерівність

.

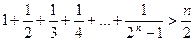Доведення. При 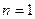отримуємо вірну нерівність 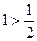. Нехай вона вірна при деякому натуральному числі 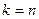, тобто нехай виконується нерівність

.

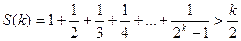Використовуючи це припущення, покажемо, що вірною є також нерівність

.

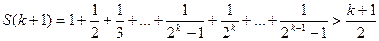Очевидно, що 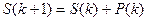, де 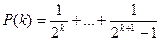. Вираз 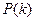являє собою суму 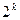дробів, кожний з яких більший, ніж 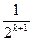. Отже,

.

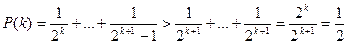Таким чином, 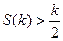(за припущенням) і 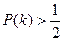. Тому 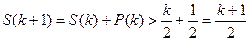, тобто 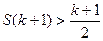. На основі принципу математичної індукції стверджуємо що задана в умові нерівність виконується для довільного натурального числа .

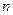Задача 1.6.5. Довести, що для довільного натурального числа 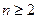та для довільних дійсних чисел 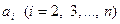виконується нерівність

.

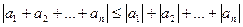Доведення. При 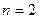нерівність 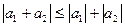вірна. Справді, вона вірна у випадку, коли одне з чисел (або обидва) рівні 0. У випадку, коли обидва числа додатні або обидва від’ємні, виконується знак рівності. Якщо ж числа різних знаків, то дістаємо строгу нерівність. Можливі і інші доведення цього факту, наприклад, аналітичним методом або методом доведення від супротивного.

Нехай нерівність вірна при деякому натуральному 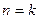, тобто виконується співвідношення 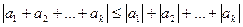. Тоді

,

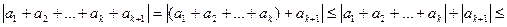
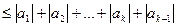що, згідно з принципом математичної індукції, завершує доведення.

Задача 1.6.6. Довести, що для 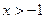при всіх натуральних 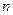виконується нерівність 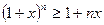(нерівність Бернуллі).

Доведення. При 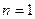виконується знак рівності, тому твердження вірне. Нехай виконується нерівність 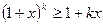. Тоді

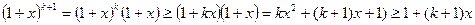
і, відповідно до принципу математичної індукції, нерівність вірна.

Задача 1.6.7. Довести методом математичної індукції, що при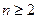

.

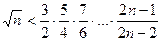Доведення. При 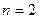отримуємо вірну числову нерівність 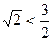. Припустимо, що вірна нерівність 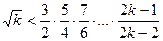і покажемо, що

.

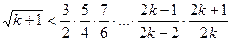Із припущення маємо 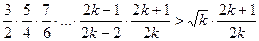. Покажемо, що 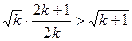. Аналізуючи різницю квадратів лівої та правої частин, дістаємо 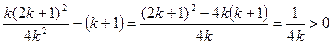, що доводить потрібне твердження. Отже, відповідно до принципу математичної індукції, нерівність доведена.

Задача 1.6.8. Довести, що 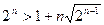для всіх натуральних .

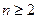Доведення. При 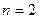отримуємо вірну числову нерівність 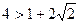. Нехай виконується нерівність 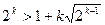. Покажемо, що звідси випливає вірність співвідношення 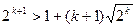. Маємо

.

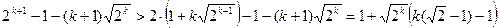Одержаний вираз додатний при 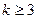. Таким чином із припущення, що нерівність вірна при 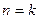випливає, що вона вірна при 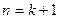. Згідно з принципом математичної індукції нерівність виконується при довільному натуральному .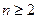