Туынды бойынша шешілмеген теңдеулер,параметр енгизу әдісі

5.1. Туынды бойынша шешілмеген теңдеулердің жалпы түрін мынандай өрнекпен жазуға болады:

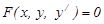(1)

мұндағы, F – кейбір 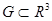облысында анықталған үздіксіз функция.

Анықтама-1. 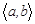аралығында анықталған 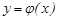функциясы (1) теңдеудің шешімі деп аталады, егер мынандай үш шарт орындалса:

1) 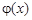функциясы 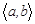аралығының барлық нүктесінде дифференциалданатын болса,

2)

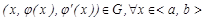
3)

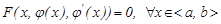
Туынды бойынша шешілген теңдеу сияқты, туынды бойынша шешілмеген теңдеу де ХОУ жазықтығында бағыттар өрісін айқындайды. Бірақ, бұл өріс жалғыз болмауы мүмкін. Себебі, (1) теңдеуді у¢ бойынша шешкенде оның бірнеше түбірлері болуы мүмкін: 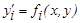. Жалпы жағдайда, (1) теңдеуді у¢ бойынша шешу мүмкін бола бермейді. Бірақ, басқа айнымалылары бойынша шешілуі мүмкін. Мұндай жағдайда параметр енгізу әдісін қолданады.

Айталық, (1) теңдеу у бойынша шешілген делік: 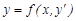. Бұл жағдайда 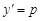параметрін енгізу арқылы

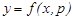(2)

теңдеуін аламыз. Осы қатынастан толық дифференциал алып, алмастырудағы 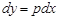байланысын ескерсек, онда мынандай теңдеу аламыз:

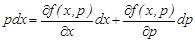(3)

немесе

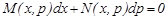(4)

Бұл теңдеу бұрын қарастырылған теңдеулердің қатарына жатады. Егер оның 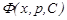жалпы интегралы белгілі болса, онда

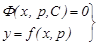(5)

түріндегі қатынастары (1) теңдеудің интегралдық қисығын анықтайды.

Дәл осы сияқты, (1) теңдеу 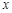бойынша шешілген болса: 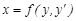, онда 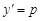параметрін енгізіп, толық дифференциал алатын болсақ:

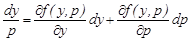(6)

теңдеуін аламыз. Бұл теңдеу де симметриялы түрге келтіріледі:

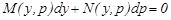(7)

Егер соңғы теңдеудің 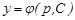шешімі белгілі болса, онда

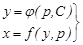(8)

қатынастары (1) теңдеудің жалпы шешімінің параметрлік түрін береді.

5.2. Параметр енгізу әдісінің ерекшелігін байқау үшін Лагранж теңдеуін қарастырайық:

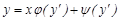(9)

Бұл теңдеуге 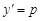( 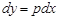) алмастыруын жасап, толық дифференциалын табайық;

.

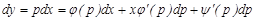Осыдан

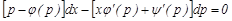
немесе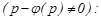

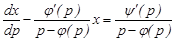(10)

түріндегі сызықтық біртексіз теңдеу аламыз. Тұрақты санды вариациялау әдісімен теңдеудің жалпы шешімін оңай жазамыз:

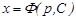
Соңғы қатынасқа бастапқы теңдеудің параметрлік түрін қосып жазсақ, жалпы шешімнің параметрлік түрін аламыз:

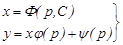(11)

Егер 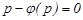болса, онда осы теңдеудің нақты шешімдерін: 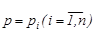, бастапқы теңдеуге қойып,

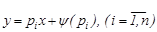(12)

түріндегі шешімдер аламыз. Бұл шешімдер ерекше шешім болуы мүмкін. Енді осы Лагранж теңдеуінің дербес түрін қарастырайық:

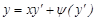(13)

Бұл теңдеуді Клеро теңдеуі деп атайды.

Жоғары айтылған әдіс бойынша 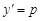белгілеуін енгізейік:

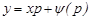(14)

Осыдан толық дифференциал тауып, 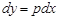қатынасын пайдалансақ, онда

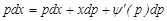
теңдігін аламыз. Ал бұдан

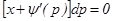(15)

Соңғы теңдеу екі теңдеуге бөлінеді:

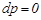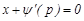және (16)

Осыдан, егер 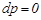болса, онда 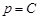. Мұны бастапқы теңдеуге апарып қойсақ,

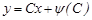(17)

түріндегі жалпы шешім аламыз.

Егер (16) теңдеудің екіншісі орын алса, онда

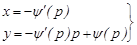(18)

түріндегі Клеро теңдеуінің параметрлік ерекше шешімін аламыз.

5.3. Енді тұйық түрде интегралданатын теңдеулерді келтірейік.

1⁰. 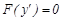(19)

Бұл теңдеудің 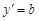түрінде нақты шешімі болуы мүмкін: 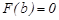. Сонда 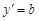қатынасын интегралдап, 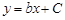өрнегін табамыз. Осыдан: 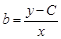. Бұл қатынасты (19) теңдеуге апарып қойсақ,

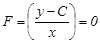(20)

түріндегі жалпы интеграл аламыз.

Мысал-1. 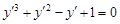теңдеуінің жалпы интегралы мына түрде жазылады:

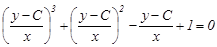
2⁰. 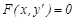(21)

Бұл теңдеуді 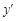бойынша шешуге мүмкіншілік болмаса, онда жаңа параметрді екі қатынаспен енгізу ыңғайлы: 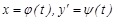. Ал 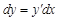болғандықтан, мынандай теңдеу жазамыз:

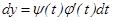
Бұдан

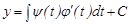
Осы өрнектің қасына 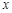-тың параметрлік түрін қосып жазсақ:

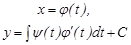(22)

түріндегі параметрлік шешімді аламыз.