Задача Коши. Теорема существования и единственности задачи Коши.
Билет 1
Соотношение вида 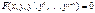 , где
, где 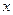 - независимый аргумент,
- независимый аргумент, 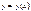 - искомая функция,
- искомая функция, 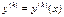 её производная порядка
её производная порядка 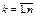 при условии, что
при условии, что 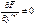 , называется обыкновенным дифференциальным уравнением (ОДУ) порядка n. Порядком ОДУ называется наивысший порядок производной, входящей в уравнение.
, называется обыкновенным дифференциальным уравнением (ОДУ) порядка n. Порядком ОДУ называется наивысший порядок производной, входящей в уравнение.
 В частности, соотношение
В частности, соотношение 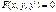 при
при 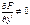 называется обыкновенным дифференциальным уравнением (ОДУ) 1-го порядка.
называется обыкновенным дифференциальным уравнением (ОДУ) 1-го порядка.
Пример.
1) 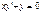 , 2)
, 2) 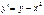 , 3)
, 3) 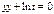 , где
, где 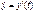 - ОДУ 1-ого порядка
- ОДУ 1-ого порядка
4) 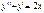 - ОДУ 2-ого порядка
- ОДУ 2-ого порядка
5) 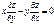 - не является ОДУ 1-ого порядка, это дифференциальное уравнение в частных производных 1-ого порядка
- не является ОДУ 1-ого порядка, это дифференциальное уравнение в частных производных 1-ого порядка
Определение 2.
Частным решением ОДУ 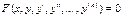 называется функция
называется функция 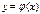 : 1) определенная на промежутке I = < α , β >, 2) принадлежащая классу Cn(I) , 3) обращающая равенство
: 1) определенная на промежутке I = < α , β >, 2) принадлежащая классу Cn(I) , 3) обращающая равенство 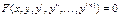 в тождество.
в тождество.
Общим решением ОДУ 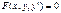 называется множество всех частных решений.
называется множество всех частных решений.
Определение 2’.
Частным решением ОДУ 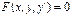 называется функция
называется функция 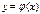 , определенная на промежутке I = < α , β >, принадлежащая классу C1(I), обращающая равенство
, определенная на промежутке I = < α , β >, принадлежащая классу C1(I), обращающая равенство 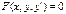 в тождество.
в тождество.
Общим решением ОДУ 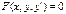 называется множество всех частных решений.
называется множество всех частных решений.
Если из уравнения 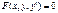 можно выразить
можно выразить 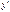 как однозначную функцию переменных
как однозначную функцию переменных 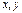 , то оно равносильно уравнению
, то оно равносильно уравнению
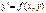 , (1)
, (1)
которое называется ОДУ 1-ого порядка, разрешенным относительно 1-ой производной.
Задачи, решаемые теорией ОДУ:
1) Отыскание всех решений ОДУ (то есть общего решения),
2) Нахождение единственного решения, если ОДУ решается с дополнительными условиями:
· А) условия Коши,
· Б) краевые условия,
· В)функциональные условия.
Определение 3.
Интегральной кривой будем называть всякую кривую, расположенную на плоскости 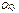 и являющуюся графиком какого-либо решения
и являющуюся графиком какого-либо решения 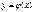 заданного ОДУ.
заданного ОДУ.
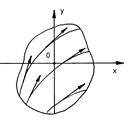
Приведём геометрическую интерпретацию решения уравнения (1).
Уравнение (1) задаёт в каждой точке 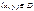 значение углового коэффициента касательной
значение углового коэффициента касательной 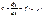 , проведённой к интегральной кривой. Если в каждой точке области
, проведённой к интегральной кривой. Если в каждой точке области  представить направление касательной в виде стрелки (вектора), то получится поле направлений. Частным решением является кривая, касательная к которой в каждой точке совпадает с построенным полем направлений.
представить направление касательной в виде стрелки (вектора), то получится поле направлений. Частным решением является кривая, касательная к которой в каждой точке совпадает с построенным полем направлений.
Определение.
Геометрическое место точек плоскости 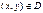 , в которых касательные к искомым интегральным кривым сохраняют постоянное направление, называется изоклиной. Уравнение изоклины имеет вид
, в которых касательные к искомым интегральным кривым сохраняют постоянное направление, называется изоклиной. Уравнение изоклины имеет вид 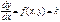 , где
, где 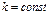 .
.
Вывод.
Чтобы приближенно построить решение уравнения 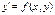 необходимо построить поле направления, провести достаточное количество изоклин, а затем провести интегральные кривые, которые в точках пересечения с изоклинами
необходимо построить поле направления, провести достаточное количество изоклин, а затем провести интегральные кривые, которые в точках пересечения с изоклинами 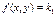 ,
, 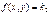 , …,
, …, 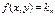 имеют касательные с угловыми коэффициентами соответственно равными
имеют касательные с угловыми коэффициентами соответственно равными 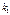 ,
, 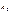 , …,
, …, 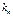 .
.
Пример.
Рассмотрим уравнение 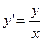 в области
в области 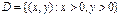 , в которой определена правая часть уравнения. Элементарная проверка позволяет убедиться, что все функции вида
, в которой определена правая часть уравнения. Элементарная проверка позволяет убедиться, что все функции вида 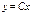 , где
, где 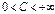 являются решениями данного уравнения. Интегральными кривыми в данной задаче будут всевозможные открытые лучи
являются решениями данного уравнения. Интегральными кривыми в данной задаче будут всевозможные открытые лучи 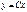 , где
, где 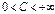 , – графики частных решений в заданной области
, – графики частных решений в заданной области 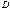 .
.
Определение 4.
Частным интегралом ОДУ называется соотношение вида 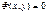 , которое определяет некоторое частное решение
, которое определяет некоторое частное решение 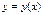 как неявную функцию аргумента
как неявную функцию аргумента 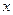 .
.
Общим интегралом ОДУ называется соотношение вида 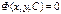 , которое при произвольном выборе параметра
, которое при произвольном выборе параметра 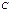 определяет некоторое частное решение
определяет некоторое частное решение 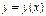 как неявную функцию аргумента
как неявную функцию аргумента 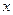 . При этом любое частное решение может быть при подходящем выборе константы
. При этом любое частное решение может быть при подходящем выборе константы 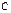 записано в виде
записано в виде 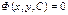 .
.
Пример.
 В предыдущем примере для ОДУ 1-ого порядка
В предыдущем примере для ОДУ 1-ого порядка 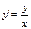 было получено общее решение:
было получено общее решение: 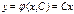 , где
, где 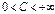 . Отсюда можно записать, что:
. Отсюда можно записать, что:  - общий интеграл, при
- общий интеграл, при 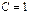 :
: 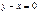 - частный интеграл,
- частный интеграл, 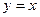 - частное решение.
- частное решение.
Определение.
Говорят, что уравнение (1) разрешимо явно, если его решение выражается через элементарные функции.
Определение.
Если решение ОДУ первого порядка выражается (в явном или неявном виде) через элементарные функции и интегралы от явно заданных функций, то оно называется решением в квадратурах, а само уравнение – разрешимым в квадратурах.
Замечание.
В теории ОДУ интегралом обычно называют решение уравнения. Чтобы избежать какой-либо путаницы, выражение 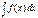 называют не интегралом, а квадратурой
называют не интегралом, а квадратурой
Определение.
Любой процесс нахождения решения ОДУ называется интегрированием дифференциального уравнения.
Задача Коши. Теорема существования и единственности задачи Коши.
Пусть задана точка 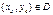
Определение 5.
Задачей Коши для уравнения, разрешенного относительно производной, называется задача
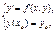 (2)
(2)
которая формулируется следующим образом:
найти решение 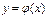 уравнения
уравнения 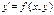 , которое удовлетворяет условию
, которое удовлетворяет условию 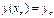 . Условие
. Условие 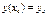 называется начальным условием, а пара чисел
называется начальным условием, а пара чисел 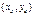 называется начальными данными или данными Коши.
называется начальными данными или данными Коши.
Геометрическая интерпретация задачи Коши: найти интегральную кривую, проходящую через заданную точку 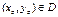 .
.
Решение задачи Коши может быть записано (с учётом начального условия):
Ø в явном виде: 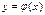
Ø в неявном виде: 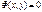
Ø в параметрической форме: 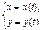
Отметим также, что решение задачи Коши (2) является частным решением уравнения (1).
Пример.
Решить задачу Коши: 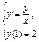
Ранее было получено общее решение 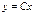 . Используя начальное условие, получаем
. Используя начальное условие, получаем 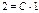
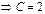 . Отсюда
. Отсюда 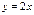 - решение данной задачи Коши.
- решение данной задачи Коши.
Обобщение понятия ОДУ.
Пусть функции P (x, y), Q (x, y) определены в области 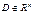 . Выражение
. Выражение
P (x, y) dx + Q (x, y) dyназывается дифференциальной формой первого порядка.
Определение 6.
Уравнение вида P (x, y) dx + Q (x, y) dy = 0 (1’)
будем называть уравнением в дифференциальной форме или уравнением в дифференциалах.
Уравнение вида (1) предполагает, что x - независимая переменная, а y (x)- является функцией x,оно сводится к виду (1’)домножением наdxи переносом 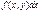 в левую часть.
в левую часть.
Уравнение вида (1’)рассматриваетxиyкак равноправные переменные, оно сводится к виду (1),если функция Q (x, y)не равна 0 в области  , надо разделить уравнение на Q (x, y) dx.
, надо разделить уравнение на Q (x, y) dx.
