Направленные отрезки. Понятие вектора

Определение. Отрезок AB называется направленным, если указано, какая из точек A или B является его началом, а какая концом.

Если A – начало, а B – конец, то этот отрезокобозначается ,а на чертеже его конец обозначается стрелочкой.

Определение. Длиной направленного отрезка называется длина отрезка AB.

Определение. Направленные отрезки и называются сонаправленными (противоположно направленными), если лучи AB и A₁B₁ сонаправлены (противоположно направлены). Пишем ­­ (­¯).

Определение. Два направленных отрезка и называются эквивалентными или равными, если они сонаправлены и имеют одинаковую длину. Пишем ~. Очевидно, ~ Û они совмещаются параллельным переносом.

Легко проверить, что данное отношение, определенное на множестве всех направленных отрезков плоскости или пространства обладает следующими свойствами:

1.~ (рефлексивность),

2.~ Û ~ (симметричность),

3.(~ & ~)Þ ~ (транзитивность).

Таким образом, отношение, которое мы определили, действительно является отношением эквивалентности (это отношение изучается в курсе алгебры). Поэтому множество всех направленных отрезков распадается на непересекающиеся классы эквивалентных друг другу отрезков.

Определение. Вектором называется класс эквивалентных между собой направленных отрезков. Другими словами, каждый направленный отрезок задает вектор, при этом, эквивалентные отрезки задают один и тот же вектор. Направление всех отрезков данного класса называется направлением вектора, а их длина – длиной вектора. Длина вектора обозначается ½½ .

Если вектор задается направленным отрезком , то пишем = , и говорим, что есть вектор , отложенный из точки A . На чертеже вектор изображается любым из задающих его направленных отрезков.

Предложение 1. Пусть задан направленный отрезок и произвольная точка A₁. Тогда существует одна и толькоодна точка B₁, такая что ~. Другими словами, данный вектор можно отложить из любой точки, и притом,единственным образом.

Упражнение. Доказательство проведите самостоятельно

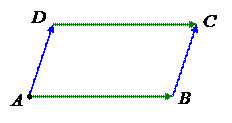Пример. Пусть ABCD – парал­лело­грамм. Тогда ~ , и поэтому эти направленные отрезки они задают один и тоже вектор. Аналогично и задают один и тот же вектор.

Определение. Вектор, длина ко-торого равна нулю, называется нулевым и обозначается . Вектор, длина которого равна 1, называется единичным.

Определение. Векторы и называются сонаправленными (противоположно направленными), если задающие их направленные отрезки сонаправлены (противоположно направлены). Пишем ­­ ( ­¯ ). Два вектора, направления которых совпадают или противоположны, называются коллинеарными. Пишем ||. Считается, что у направление неопределено и он коллинеарен любому вектору. Три и более векторов, параллельных одной плоскости называются компланарными.

Операции над векторами.

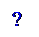
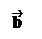
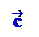
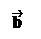
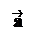
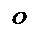
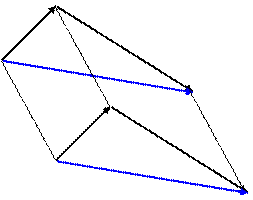Определение. Пусть заданы два вектора и . Отложим вектор от произвольной точки O: = , а из точки A отложим вектор : = . Пусть – вектор, который задается направленным отрезком . Тогда называется суммой векторов и .

Пишем = + .

Этот способ построения суммы двух векторов называется правилом треугольника.

Однако, в нашем определении использо­валась произвольная точка O. Возникает вопрос: что если мы начнем построение от другой точки O₁? Не получится ли другой вектор ? Другими словами, требуется еще доказать, что наше определение корректно. Самостоятельно докажите, пользуясь чертежом, что (~ & ~) Þ ~.