Операции над векторами и их свойства

1. Сложение

А)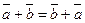

Б)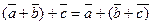

В)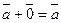

Г)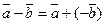

Противоположные вектора – вектора модули которых равны, но направление противоположное.

19.

1. Умножение вектора на число

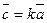, если а)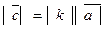

Свойства

1.

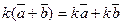
2.

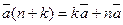
3.

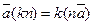
4.

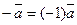
Орт вектора –единичный вектор сонаправленный с данным вектором.

20.

Ось –прямая с заданным направлением.

Проекция точки – основание перпендикуляра, опущенного из точки на ось.

Пр_eAB=|AB| или -|AB|

Свойства проекции.

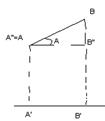
1. Пр_еAB=|AB|cosA

Доказательство: 1.A-острый Из треуг. ABB’’: |AB’’| =|AB|cosA

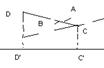2. A-тупой B=180-A |CC’|=|DC|cosB=|DC|cos(Pi-A)=-|DC|cosA =>

=>|D’C’|=-|DC|cosA

2. Пр_еAB+Пр_еВС=Пр_е(АВ+ВС)

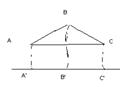Доказательство:

1.А₁-угол между AB и e A₂ – угол между ВС и е острые

Пр_еАВ=|А’В’| Пр_еВС=|В’С’ | Пр_е(АВ+ВС)=|В’С’|+|А’В’| =|A’C’|

2.А₁- острый A₂ – тупой

Пр_еАВ=|А’В’| Пр_еВС=-|В’С’ | Пр_е(АВ+ВС)=|В’С’|-|А’В’| =|A’C’|

3.k*Пр_ea=Пр_еka

Доказательство:

1. K>0 => ka||a => угол не меняется

Пр_еа=|a|cosA Пр_еka=|ka|cosA=|k|Пр_еа

2. K<0 => угол между ka и e =Pi-A

Пр_eka=|ka|cos(Pi-A)=|k||a|(-cosA)=-|k||a|cosA=kПр_ea

21.

ab=|a||b|cosA

Свойства

1. Пр_еа=|a|cosA=ab/|b|

Пр_аb=|b|cosA =>ab/|a|

=>ab=|b|Пр_ba=|a|Пр_аb

2. a(b+c)=ab+ac

Доказательство: ab=|a|Пр_ab ac=|a|Пр_ас

Пр_а(b+c)=Пр_аb +Пр_ас =>|a|Pr_a(b+c)=|a|Pr_ab+|a|Pr_aс => a(b+c)=ab+ac

3. (na)b=a(nb)=n(ab)

Доказательство: a(nb)=|a|Pr_abn=|a|nPr_ab=n(ab)

4. Два ненулевых вектора а≠0, b≠0 перпендикулярны когда ab=0 и наоборот.

Доказательство: 1. если a┴b, то угол A=90^o => cosA=0 , то ab=0

5. Связь между длиной вектора и скалярным произведением.

Aa=|a||a|=|a|²=> |a|=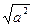

22.

c=axb, если

1. |c|=|a||b|sinA

2. c┴a c┴и

3. a b с образуют первую тройку векторов

Свойства

1. геометрический смысл S=axb
2. axb=-bxa
3. ax(b+c)=axb+cxa
4. Умножение вектора на число (na)xb=ax(nb)=n(axb)

23.

Смешанное произведение векторов

C(axb)=a(bxc)=abc

V=abc

24.

Признак коллинеарности векторов

a\\b то существует k≠0? Что b=ka

Доказательство:

1. Если b=ka =>b||a, по определению умножения вектора на число.
2. Пусть b||a , возьмем k=|b|/|a|

Если а||b то k=|k|

Если a||b то k=-|k|

Тогда с=ka будет с=b, т.е. b=ka, c=ka

a) |c|=|k||a|

b) c||a

c) c||a, если k>0

d) c||a, tckb k<0

Теорема.

Если 2 вектора коллинеарные то они линейно зависимы.

Доказательство:

По признаку коолинеарности: a=kb a-kb=0

1. a≠0, b≠0 тогда a и b ЛЗ l₁=1, l₂=-k
2. а=0, тогда l₁=1, l₂=0 – ЛЗ

Два ненулевых вектора а≠0, b≠0 перпендикулярны когда ab=0 и наоборот.

Доказательство: 1. если a┴b, то угол A=90^o => cosA=0 , то ab=0

3 вектора компланарны если лежат в одной плоскости т.е. их смешанное произведение равно 0.

25.

Векторы a₁ a₂…a_n называются ЛЗ если существуют n₁ n₂…n_n, где хотя бы одно n_i≠0, что n₁a₁+n₂a₂+…+a_nn_n=0, если это условие выполняется при всех n=0 то векторы ЛНЗ

Базисомв некотором пространстве называется набор из n ЛНЗ векторов a₁ a₂…a_n, такой что любой вектор b из этого пространства можно представить как линейную комбинацию базисных векторов т.к. существуют числа n₁ n₂…n_n b=n₁a₁ +n₂a₂+…+n_na_n

26.

Теорема.

Если 2 вектора коллинеарные то они линейно зависимы.

Доказательство:

По признаку коолинеарности: a=kb a-kb=0

1. a≠0, b≠0 тогда a и b ЛЗ l₁=1, l₂=-k
2. а=0, тогда l₁=1, l₂=0 – ЛЗ

В соответствии с этой теоремой получаем что если вектора неколлинеарны то они ЛНЗ.

28.