Интервалы прогноза по линейному уравнению регрессии

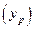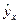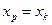В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз при , т. е. путем подстановки в уравнение регрессии 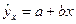соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки 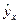, т. е. 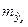, и соответственно интервальной оценкой прогнозного значения .

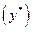Чтобы понять, как строится формула для определения величин стандартной ошибки 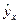,обратимся к уравнению линейной регрессии: 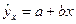. Подставим в это уравнение выражение параметра :

,

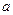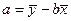тогда уравнение регрессии примет вид:

.

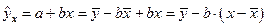Отсюда вытекает, что стандартная ошибка 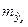зависит от ошибки 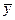и ошибки коэффициента регрессии 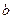, т.е.

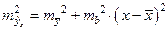
Из теории выборки известно, что 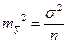. Используя в качестве оценки 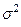остаточную дисперсию на одну степень свободы 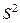,получим формулу расчета ошибки среднего значения переменной :

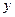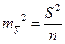
= 3,34.

Ошибка коэффициента регрессии, как уже было показано, определяется формулой

.

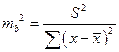Считая, что прогнозное значение фактора 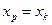,получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т. е. :

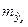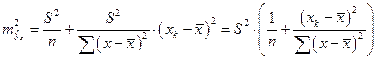
Соответственно 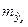имеет выражение

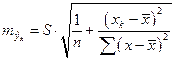
Рассмотренная формула стандартной ошибки предсказываемого среднего значения 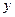при заданном значении 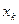характеризует ошибку положения линии регрессии. Величина стандартной ошибки 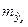, как видно из формулы, достигает минимума при 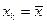и возрастает по мере того, как «удаляется» от 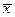в любом направлении. Иными словами, чем больше разность между 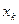и 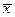, тем больше ошибка 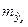, с которой предсказывается среднее значение 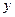для заданного значения 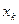. Можно ожидать наилучшие результаты прогноза, если признак-фактор 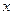находится в центре области наблюдений 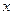,и нельзя ожидать хороших результатов прогноза при удалении 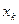от 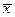. Если же значение 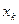оказывается за пределами наблюдаемых значений 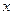, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько 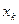отклоняется от области наблюдаемых значений фактора .

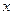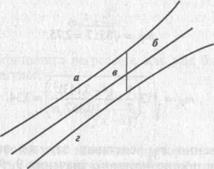На графике доверительные границы для 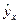представляют собой гиперболы, расположенные по обе стороны от линии регрессии.

Однако ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку 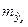, но и случайную ошибку S.

Средняя ошибка прогнозируемого индивидуального значения 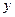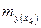составит:

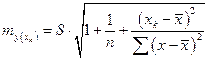
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора 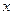. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора.

Рассмотренная формула средней ошибки индивидуального значения признака 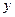может быть использована также для оценки существенности различия предсказываемого значения исходя из регрессионной модели и выдвинутой гипотезы развития событий.