Лекція 4: Наближені методи розв'язування систем лінійних алгебраїчних рівнянь

1. Постановка задачі

2. Метод простої ітерації

3. Метод Зейделя

Розв`язування систем лінійних рівнянь являється однією із найважливіших задач, які часто зустрічаються як в прикладній математиці, так і в спеціальних загально інженерних дисциплінах.

Часто при розв`язуванні системи зручно користуватися наближеними методами, які потребують меншої затрати праці та обчислення і які дають послідовність наближених значень, що збігається до шуканого розв`язку. До таких методів належить і метод ітеракції.

Метод простої ітерації. Для простоти розберемо застосування методу ітеракцій при розв`язуванні системи трьох рівнянь з трьома невідомими. Будемо вважати, що система має єдиний розв`язок, тобто визначник її 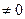. Нехай система трьох рівнянь з трьома невідомими якимось чином приведена до вигляду 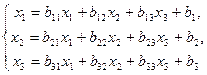(1)

Систему (1) називають приведеною системою. Процес інтеграції будується для приведеної системи.

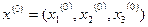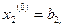
Довільно вибираємо початкове (нульове) наближення . Наприклад, 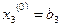(тобто в якості початкового наближення вибрані вільні члени системи). Підставимо 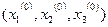в праву частину рівнянь системи (1) і приймемо одержані числа за перше наближення 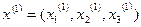, тобто

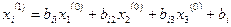(і=1,2,3).

Аналогічно по першому наближенню визначаємо друге 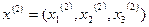: 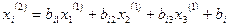(і=1,2,3) і так далі. В загальному випадку по (n-1)-му наближенню 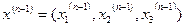знаходимо n-те наближення 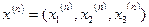по формулах

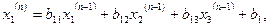
(2)

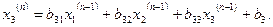
Аналогічно застосовується метод ітеракцій для системи n рівнянь з n невідомими.

ПРИКЛАД!: Знайти друге наближення до розв`язування системи

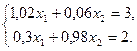
Розв`язування: Складемо із заданої системи приведену:

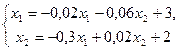
(очевидно, що це можна виконувати різними шляхами).

В якості початкового наближення вибираємо вільні члени 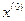=(3;2) і обчислюємо по формулах (2) :

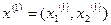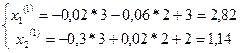
Далі визначаємо :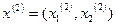

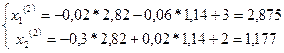
Обґрунтування методу: Для обґрунтування методу відмітимо, що якщо побудований процес збігається, то границя являється розв`язком шуканої системи. Для того, щоб впевнитись в цьому, достатньо перейти до границі в обох частинах рівнянь системи (2).

В теорії обчислювальних методів доведено, що достатні умови збіжності процесу ітеракцій полягають в тому, що для приведеної системи повинно бути виконане одне з умов 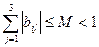(і=1,2,3), (3)

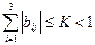(j=1,2,3), (4)

тобто або сума модулів коефіцієнтів кожного приведеного рівняння (умова(3)), або сума модулів коефіцієнтів при кожному невідомому у приведеній системі (умова(4)) менша одиниці.

В розглянутому прикладі 1 виконані дві достатні умови:

1) , ;

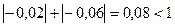2) , .

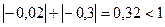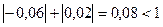Відомо, якщо визначник системи відмінний від нуля, то із неї завжди можна9але не завжди просто) побудувати приведену систему, що задовільняє одному із достатніх умов (3) або (4). Це легко зробити, якщо модулі діагональних коефіцієнтів системи перевищують суму модулів решту коефіцієнтів відповідних рядочків. Дійсно, нехай

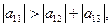
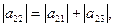
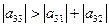(5)

або 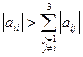(і=1,2,3).

Із системи трьох рівнянь з трьома невідомими виразимо відповідно 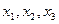. Одержимо

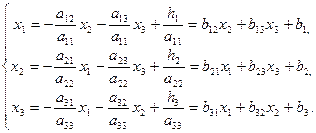(6)

Тоді, враховуючи (5), маємо 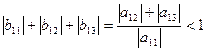і так далі, тобто виконана умова (3).

Таким чином, якщо коефіцієнти системи з трьох рівнянь з трьома невідомими задовольняють умові (5), то із неї можна побудувати приведену систему виду (6), і процес ітеракцій для цієї системи буде збіжним. Умова (5) являється достатньою умовою збіжності процесу ітеракцій системи.

Якщо умова (5) не виконується ( або виконується не для всіх рівнянь), то систему трьох рівнянь з трьома невідомими можна привести до еквівалентної, але вже з виконанням умови (5) для всіх діагональних елементів. Цього добиваються підбором лінійних комбінацій рівнянь системи і відповідною перестановкою рівнянь. Пояснимо це на наступному прикладі.

ПРИКЛАД2: Задану систему рівнянь привести до еквівалентної, для діагональних елементів якої виконана умова (5)

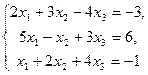
Розв`язання: Аналізуємо послідовно рівняння системи. Для першого рівняння умова (5) не виконується ні для одного із коефіцієнтів. Для другого рівняння маємо 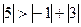і умова (5) виконується для першого коефіцієнта. Тому друге рівняння запишемо першим в еквівалентній системі. Для третього рівняння 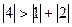і воно буде третім в еквівалентній системі

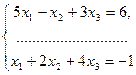
Тепер треба підібрати друге рівняння так, щоб в ньому для коефіцієнта при х була виконана умова (5) і воно являлось лінійною комбінацією заданих рівнянь, причому для одержання лінійної комбінації обов`язково повинно використовуватися перше рівняння. Додавши перше із заданих рівнянь до третього, одержимо друге рівняння, яке буде володіти потрібною властивістю. Єквівалентна система, коефіцієнти якої задовольняють умову (5), має вигляд: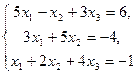

а приведена система

І так будь-яку систему при визначнику відмінному від нуля можна привести до еквівалентної, що задовільняє умові (5), із якої по формулам (6) одержується приведена система. Для останньої будується процес ітеракцій по формулах (2).

Звичайно, вказана процедура перетворення системи до приведеної з виконанням умови (3) далеко не єдина (див. приклад 1). Вияснимо питання про оцінку похибки наближень, одержаних по формулах (2).

Із теорії обчислювальних методів відомо, що оцінка похибки n-го наближення 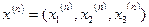, тобто оцінка різниці 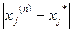(j=1,2,3), визначається однією із формул:

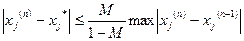(j=1,2,3),

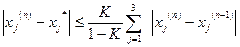(j=1,2,3).

В частковому випадку, при М 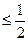(або К 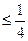) одержимо

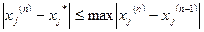(j=1,2,3).

Тоді оцінка похибки n-го наближення зводиться до оцінки модуля різниці двох послідовних наближень. В загальному чим менше М<1 (або К<1), тим менше треба виконувати ітеракцій для одержання результату з допустимою похибкою (тим швидше збігається ітеракційний процес).

Метод Зейделя

Цей метод представляє собою деяке видозмінення методу простої ітеракції. В методі простої ітерації при обчисленні n-го наближення 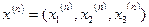ми користувались тільки результатом (n-1)-го наближення. В методі ж Зейделя при обчисленні значення х 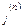користуються вже обчисленими значеннями х 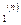,...,х 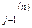, тобто якщо процес ітеракцій будується для приведеної системи, тобто n-те наближення х 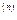при відомому (n-1)-му обчислюється по формулах

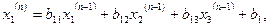
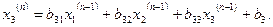
Умови збіжності методу Зейделя такі самі, як в методі звичайної ітерації, але часто він дає кращу збіжність (скоріше приводить до результату заданої точності).