Диагностическая контрольная работа. По алгебре и началам анализа
По алгебре и началам анализа.
«Производная функции. Приложения производной»
Вариант 8
Запишите вариант правильного ответа заданий уровня А
А1.Найдите производную функции f(x)=7x+ex-7.
| а) xln7+x | б) 7xln7+ex | в) 7x+1-ex ·lge | г) 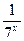 -3 -3 |
А2.Найдите производную функции h(x)=tgx+2sin x.
а) 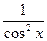 -cos x -cos x | б) ctg x+cosx | в) 3cos x+2 | г) 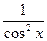 +2cos x +2cos x |
А3.Укажите первообразную функции f(x)=2sin x.
| а) cos x | б) sin2 x | в) -2cos x | г) cos 2x |
А4.Найдите  (-1), если f(x)=
(-1), если f(x)= 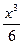 -0,5x2+2.
-0,5x2+2.
| а) -2,5 | б) 1,5 | в) -1,5 | г) 2,5 |
А5.Найдите производную функции f(x)= 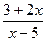 .
.
а) - 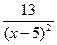 | б) 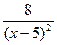 | в) 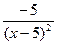 | г) 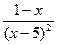 |
А6.Найдите производную функции y=x4(x3-3) в точке x0=-1.
| а) 7 | б) 5 | в) -5 | г) 19 |
А7.Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=2+x-2x4 через его точку с абсциссой x0=1.
| а) -1 | б) -7 | в) 3 | г) 0 |
А8.Найдите тангенс угла наклона касательной к графику функции y=lnx+ 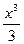 в точке с абсциссой равной 2.
в точке с абсциссой равной 2.
а) 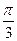 + ln2 + ln2 | б) 4 | в) 4,5 | г) 6 |
А9.Абсцисса точки минимума функции y=-x3+x2+x равняется.
| а) -1 | б) - 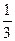 | в) 0 | г) 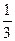 |
А10.Найдите наименьшее значение функции y= 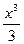 -x2-3x-1 на отрезке [-3;1].
-x2-3x-1 на отрезке [-3;1].
| а) -3 | б) 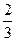 | в) -10 | г) -12 |
А11.Вычислите площадь фигуры, ограниченной линиями y=x2-4x+5 x=1, x=4 и y=0.
а) 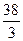 | б) 6 | в) 18 | г) 48 |
А12.К графику функции y=2x проведена касательная в точке с абсциссойx0=3.Как расположена точка пересечения этой касательной с осью OX?
| а) правее точки (4;0) | б) в точке (3;0) |
| в) левее точки (0;0) | г) левее точки (3;0) |
