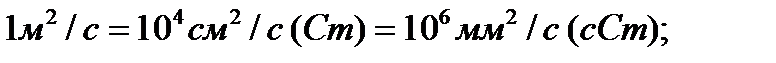Давление жидкости на криволинейную стенку
Задачи
| Задача 4.1 Построить эпюру избыточного гидростатического давления воды, определить силу полного давления и направление ее на цилиндрический затвор. Диаметр затвора d = 2 м, глубина воды Н =1,6 м, длина затвора l = 3 м. |
| Задача 4.2 Определить силу гидростатического давления воды на b = 1 м ширины криволинейной части сооружения, если H =1,5 м , r = 0,5 м . |
| Задача 4.3 Определить величину и направление силы давления воды на l =1 м ширины затвора, представляющего собой четверть кругового цилиндра радиуса R =1 м при Н = 2 м . |
Задача 4.4 Круглое отверстие в дне резервуара с водой диаметром d = 0,4 м перекрывается клапаном – полусферой радиуса r = 0,2 м . Определить: · силу Т, необходимую для поднятия клапана, при напоре h = 2 м , если вес клапана G = 200 H , а давление на свободной поверхности 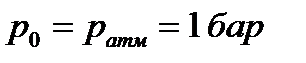 . · при каком значении h′ клапан откроется автоматически, если . · при каком значении h′ клапан откроется автоматически, если 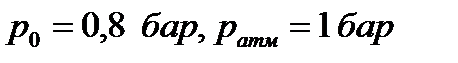 . . |
| Задача 4.5 Определить величину и направление силы полного давления воды на b =1 м ширины вальцевого затвора диаметром d =1,5 м . |
Задача 4.6 Цилиндр, радиусом r = 0,25 м и длиной 1м перекрывает отверстие размером a×b = 0,3×1 м в дне резервуара. Определить: 1.Силу давления воды на цилиндр при H = 3 м 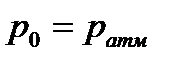 ,. 2. При какой глубине H цилиндр всплывает, если его вес G = 600 H , а давление на свободной поверхности ,. 2. При какой глубине H цилиндр всплывает, если его вес G = 600 H , а давление на свободной поверхности 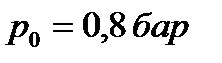 . Атмосферное давление . Атмосферное давление 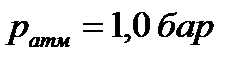 . . |
Задача 4.7 Конический клапан высотой h , изготовленный из стали удельного веса . 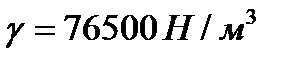 , закрывает отверстие в дне бака с водой. Определить силу R , необходимую для подъема клапана. , закрывает отверстие в дне бака с водой. Определить силу R , необходимую для подъема клапана. |
| Задача 4.8 Цилиндрический затвор имеет диаметр d и длину L . Определить величину и направление силы P полного гидростатического давления воды. |
Закон Архимеда. Плавание тел
Задачи
Задача 5.1
Бетонная плита весит в воздухе G1 = 1230 H , а в воде G2 = 735 H . Определить удельный вес бетона.
Задача 5.2
По окончании погрузки 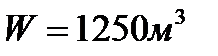 песка осадка баржи увеличилась на h =1 м . Определить удельный вес песка, если площадь плоскости плавания баржи
песка осадка баржи увеличилась на h =1 м . Определить удельный вес песка, если площадь плоскости плавания баржи 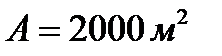 .
.
Задача 5.3
В воде плавает бревно объема 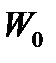 . Определить погруженную часть его объема
. Определить погруженную часть его объема 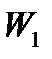 , если удельный вес дерева
, если удельный вес дерева 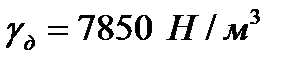
Задача 5.4
Найти объем воды 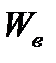 , вытесняемый баржей емкостью
, вытесняемый баржей емкостью 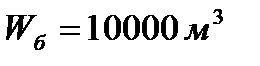 , груженой нефтью удельного веса
, груженой нефтью удельного веса 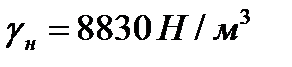
Задача 5.6
Определить вес груза, установленного на круглом в плане металлическом понтоне диаметром d = 4 м, если после установки груза осадка понтона увеличилась на h = 0,6 м .
Задача 5.7
Человек поднимает в воздухе стальной шар, вес которого 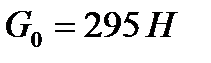 . Какого веса стальной шар может быть поднят под водой?
. Какого веса стальной шар может быть поднят под водой?
Задача 5.8
Стальной трубопровод внешнего диаметра D с толщиной стенки δ =10 мм при прокладке через реку опущен в воду. При каком значении D подъемная сила воды будет равна весу трубы? Задачу решить для трубы длиной l=1 м. Удельный вес стали  .
.
Задача 5.9
Дюкер, выполненный из стальных труб диаметром d = 0,5 м c толщиной стенки 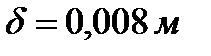 , должен опускаться на дно реки без заполнения водой. Определить необходимый объем балласта (дополнительного бетонного груза)
, должен опускаться на дно реки без заполнения водой. Определить необходимый объем балласта (дополнительного бетонного груза) 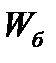 для обеспечения затопления 1м длины трубопровода. Плотность бетона
для обеспечения затопления 1м длины трубопровода. Плотность бетона 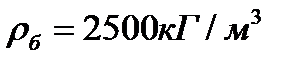 .
.
Задача 5.10 Ареометр, изготовленный из полой стеклянной трубки, снабжен внизу шариком с дробью. Внешний диаметр трубки d = 0,03 м , объем шарика 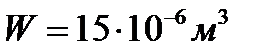 , вес ареометра , вес ареометра 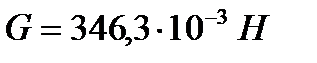 . Определить глубину h , на которую погрузится ареометр в спирт удельного веса . Определить глубину h , на которую погрузится ареометр в спирт удельного веса 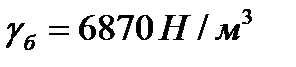 . . |
Задача 5.11
Объем надводной части айсберга равен 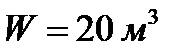 . Определить общий объем айсберга и глубину его подводной части h , если в плане он имеет форму прямоугольника размером 3× 6 м. Удельный вес льда
. Определить общий объем айсберга и глубину его подводной части h , если в плане он имеет форму прямоугольника размером 3× 6 м. Удельный вес льда 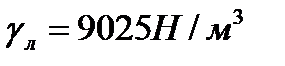 , удельный вес морской воды
, удельный вес морской воды 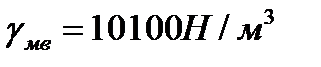 .
.
Задача 5.12
Определить, какой вес должен иметь батискаф, чтобы достигнуть глубины H =1400м при диаметре корпуса D = 3м и длине L = 6 м. На поверхности плотность морской воды составляет 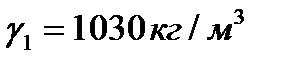 , температура
, температура 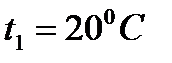 . Температура воды на глубине 1400 м
. Температура воды на глубине 1400 м 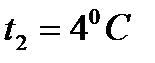 . Коэффициент объемного сжатия воды
. Коэффициент объемного сжатия воды 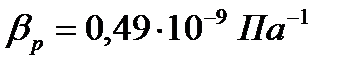 , коэффициент температурного расширения воды
, коэффициент температурного расширения воды 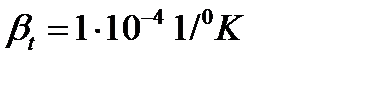
Задача 5.13 Прямоугольная баржа длиной L =18м и шириной b = 9 м загружена песком ровным слоем высотой h . Осадка баржи с песком H = 0,5м. Определить объем песка 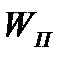 , если его относительная плотность δ = 2 , и высоту слоя песка h . Массу баржи не учитывать. , если его относительная плотность δ = 2 , и высоту слоя песка h . Массу баржи не учитывать. |
Задача 5.14
Деревянный брус длиной L = 5м, высотой h = 0,3м и шириной b = 0,3м плавает в воде с осадкой Н.
Определить осадку Н бруса, если относительная плотность его материала δ = 0,7 , а так же сколько человек (n) средней массой m = 67,5 кг могут встать на этот брус, чтобы его осадка составила H = h = 0,3м.
Задача 5.15
Объемное водоизмещение подводной лодки 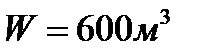 . Для погружения лодки ее отсеки нужно заполнить морской водой в количестве
. Для погружения лодки ее отсеки нужно заполнить морской водой в количестве 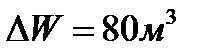 . Относительная плотность морской воды δ =1,025. Определить какая часть объема лодки
. Относительная плотность морской воды δ =1,025. Определить какая часть объема лодки 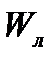 будет погружена в воду при
будет погружена в воду при  и чему равен вес лодки Gл при
и чему равен вес лодки Gл при 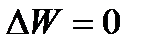 .
.
6. Равновесие жидкости в движущемся сосуде
Задачи
Задача 6.1
Железнодорожная цистерна, заполненная нефтепродуктом движется со скоростью 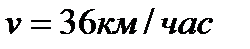 по горизонтальному закруглению радиуса r=300 м . Определить угол
по горизонтальному закруглению радиуса r=300 м . Определить угол 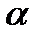 наклона свободной поверхности нефти в цистерне.
наклона свободной поверхности нефти в цистерне.
Задача 6.2 Открытая цистерна заполнена жидкостью до уровня 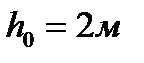 . Длина цистерны L = 20 м. Определить высоту H борта цистерны из условия отсутствия перелива жидкости при движении цистерны по горизонтали с ускорением . Длина цистерны L = 20 м. Определить высоту H борта цистерны из условия отсутствия перелива жидкости при движении цистерны по горизонтали с ускорением 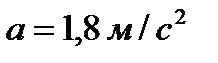 |
Задача 6.3
Определить полное избыточное давление на крышку АВ и дно СЕ цилиндрического заполненного жидкостью сосуда. Сосуд герметически закрыт и вращается вокруг вертикальной оси с угловой скоростью 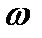 . Удельный вес жидкости −
. Удельный вес жидкости − 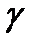 .
.
Задача 6.4
Насколько увеличится давление жидкого чугуна в точке А вследствие вращения формы при отливке, если: диаметр колеса D = 1 м , удельный вес чугуна 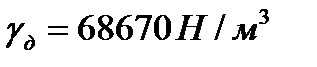 , угловая скорость , угловая скорость  . . |
Задача 6.5
| Сосуды, имеющие форму кубов с ребром a , вращаются в горизонтальной плоскости вокруг вертикальной оси. Радиус вращения равен R . Определить число оборотов n , при котором ближайшая к оси вращения грань куба обнажится от воды, а противоположная будет полностью смочена. |
Задача 6.6
Цилиндрический открытый сосуд с водой вращается вокруг вертикальной оси с постоянной угловой скоростью ω . Диаметр сосуда D = 0,8 м. Определить угловую скорость вращения 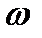 и число оборотов n сосуда, при которых глубина воронки и число оборотов n сосуда, при которых глубина воронки 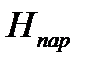 (высота параболоида вращения) была бы не более 0,9 м, а также линейную скорость u частиц воды у боковой поверхности сосуда и давление (высота параболоида вращения) была бы не более 0,9 м, а также линейную скорость u частиц воды у боковой поверхности сосуда и давление 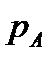 в точке А на плоскости в точке А на плоскости 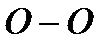 , если , если 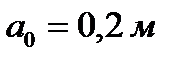 , , 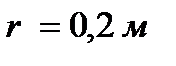 . . |
Приложение 1
Плотность, вязкость, коэффициенты объемного расширения и сжатия
некоторых жидкостей
(при 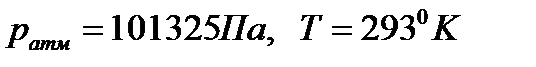 )
)
| Наименование жидкости | Плотность 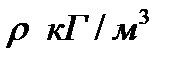 | Динамический коэффициент вязкости 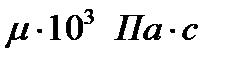 | Кинематический коэффициент вязкости 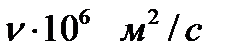 | Коэффициент объемного расширения 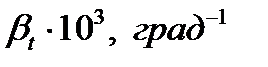 | Коэффициент объемного сжатия 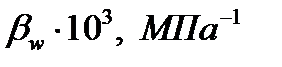 |
| Вода | 998,2 | 1,0 | 1,006 | 0,05 | 0,49 |
| Этиловый спирт | 1,2 | 1,52 | 1,1 | 0,78 | |
| Ртуть | 1,54 | 0,114 | 0,18 | 0,039 | |
| Глицерин | 0,49 | 0,25 | |||
| Керосин | 2,05 | 2,5 | 0,96 | 0,77 | |
| Бензин | - | 0,55 | - | - | |
| Диз.топливо | - | 4,0 | - | - | |
| Воздух | 1,2 | 0,0179 | 14,9 | - | - |
| Метан | 0,668 | 0,0111 | 16,6 | - | - |
Соотношения между единицами измерения
а) давления
| Единицы | 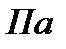 | 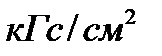 | 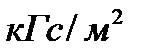 |  | 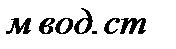 | 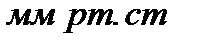 |  |
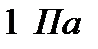 | 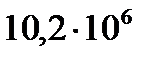 | 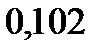 | 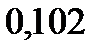 | 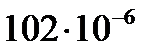 | 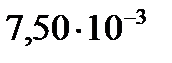 | 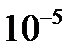 | |
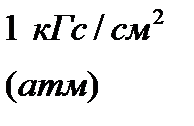 | 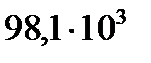 | 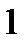 | 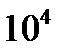 | 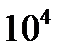 | 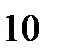 | 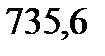 | 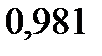 |
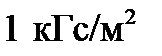 | 9,81 | 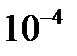 | 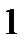 | 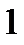 | 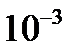 | - | - |
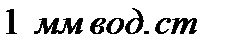 | 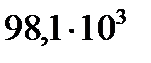 | 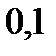 |  | 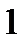 | 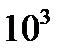 | 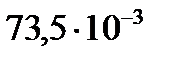 | 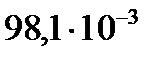 |
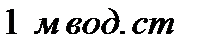 | 133,3 | 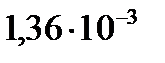 | 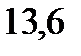 | 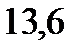 |  | 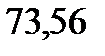 | 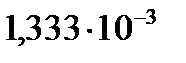 |
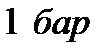 | 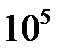 |  | 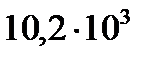 | 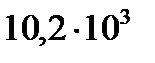 | 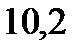 | 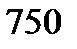 | 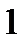 |
б) кинематической вязкости: