Элементы дифференциального исчисления

ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ ПИСЬМЕННОГО КОНТРОЛЬНОГО ЗАДАНИЯ

Для студентов дневного отделения специальностей

Юриспруденция

Выбор варианта осуществляется по приведенной ниже таблице. В первом столбце найдите свой номер в списке группы. Цифры в строке показывают номера задач из 8 предложенных заданий, которые следует решить. Например, первый в списке решает 1-ю задачу из первого задания, 3-ю — из второго, 2-ю — из третьего и т. д.

Задания выполняются в том порядке, в котором они приведены ниже. Вам необходимо выполнить по возможности максимальное количество заданий. Максимальное количество баллов за все ПКЗ — 100 баллов.

№ в списке	Номер задания

Элементы теории множеств

1. Пусть 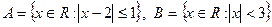. Записать множества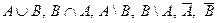

Найти область определения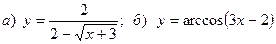

2. Пусть . Записать множества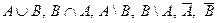

Найти область определения

3. Пусть 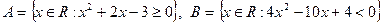. Записать множества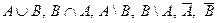

Найти область определения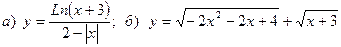

4. Пусть 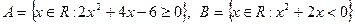. Записать множества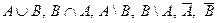

Найти область определения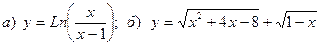

5. Пусть 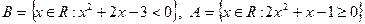. Записать множества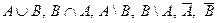

Найти область определения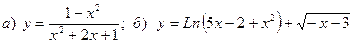

6. Пусть 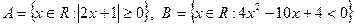. Записать множества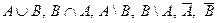

Найти область определения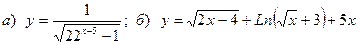

7. Пусть 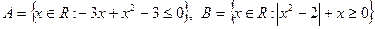. Записать множества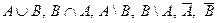

Найти область определения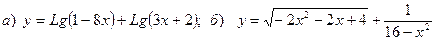

8. Пусть 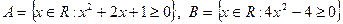. Записать множества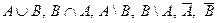

Найти область определения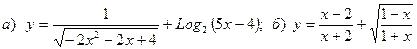

9. Пусть 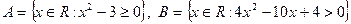. Записать множества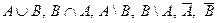

Найти область определения

10. Пусть 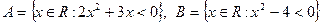. Записать множества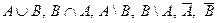

Найти область определения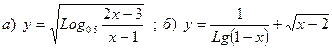

Элементы математической логики

1. Построить таблицу истинности дли формулы .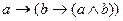

2. Доказать, что 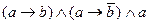тождественно ложная формула.

3. Определить, кто из четырех студентов сдал экзамен, если известно, что:

1) если первый сдал, то и второй сдал;

2) если четвертый сдал, то и первый сдал;

3) если второй сдал, то третий сдал или первый не сдал;

4) если четвертый не сдал, то первый сдал, а третий не сдал.

4. Определить истинность формулы .

5. Истинно или ложно высказывание 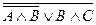, если В и С истинны?

6. Составить таблицу истинности, доказать, что следующая формула является тавтологией: .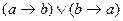

7. Учащимся объявили: в понедельник будет один урок физики и одни математики, причем, если на первом математики не будет, то физика будет на втором уроке; если третий урок не математика, то четвертый физика; а если математика будет на первой уроке, то физика пятом». Определите, на каком уроке будет физика и на каком математика.

8. Определить истинность формулы .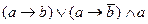

9. Доказать эквивалентность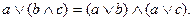

10. Истинно или ложно высказывание 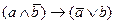, если а и b истинны?

Элементы дифференциального исчисления

1. Вычислить предел

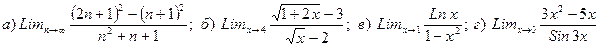
Найти производную

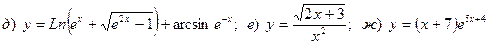
2. Вычислить предел

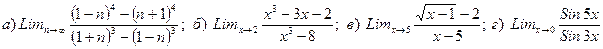
Найти производную

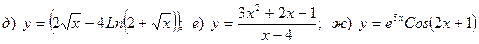
3. Вычислить предел

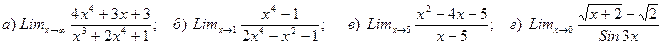Найти производную

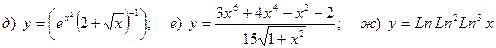
4. Вычислить предел

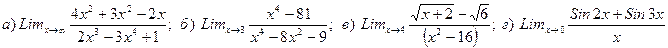Найти производную

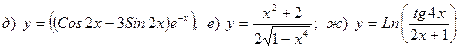
5. Вычислить предел

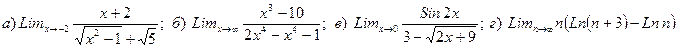Найти производную

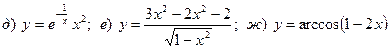
6. Вычислить предел

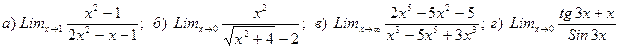
Найти производную

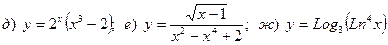
7. Вычислить предел

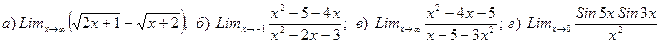Найти производную

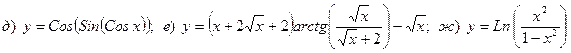
8. Вычислить предел

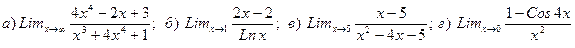
Найти производную

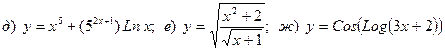
9. Вычислить предел

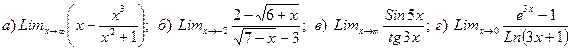
Найти производную

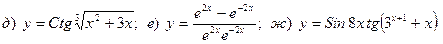
10. Вычислить предел

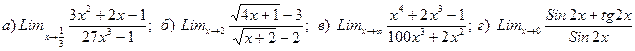Найти производную

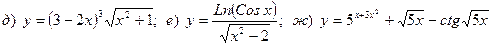
Элементы комбинаторики

1. Сколько различных четырехзначных чисел можно составить из цифр 7, 2, 4, 9, если каждая цифра используется в записи числа только один раз?

2. В домоуправлении трудится 6 человек. Поступило распоряжение о премировании трех сотрудников (различными суммами). Сколькими способами можно это сделать?

3. Анкета по изучению общественного мнения содержит 10 вопросов, на каждый из которых отвечающий дает один из трех ответов: «да», «нет», «не знаю». Найти число всех различных способов заполнения анкеты.

4. В урне 10 белых и 5 черных шаров. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы один шар оказался белым, а два шара черными.

5. В урне 10 белых и 5 черных шаров. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы все три шара оказались белыми;

6. В урне 10 белых и 5 черных шаров. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы все три шара оказались черными

7. В урне 10 белых и 5 черных шаров. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы два шара оказались белыми, а один черным;

8. Студенты одной группы должны сдать 3 экзаменов в течение двадцати дней. Сколькими способами можно составить расписание экзаменов, если в один день разрешается сдавать не более одного экзамена?

9. Игральная кость брошена два раза. Какова вероятность того, что сумма выпавших очков равна 7?

10. Для проведения экзамена по информатике создается комиссия из двух преподавателей. Сколько различных комиссий можно составить из пяти преподавателей?

Теория вероятности

1. Найти вероятность того, что трехзначный номер случайно встреченного автомобиля состоит из одинаковых цифр.

2. Программа экзамена содержит 30 вопросов. Студент знает 20 из них. Каждому студенту предлагают 2 вопроса, которые выбираются случайным образом. Положительная оценка ставится в том случае, если студент правильно ответил хотя бы на один вопрос. Какова вероятность успешной сдачи экзамена?

3. Вгруппе 30 студентов, из которых отличников - 8, хорошистов - 13 и слабо успевающих - 9. На экзамене по математике отличники могут получить только оценки "5", хорошисты могут получить с равной вероятностью оценки "4" и "5", слабо успевающие могут получить с равной вероятностью оценки "3", "4" и "5". Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что он получит оценку не ниже "4".

4. Впачке 10 тетрадей, 8 из которых в клетку. Найти вероятность того, что среди взятых наудачу двух тетрадей есть хотя бы одна в клеточку.

5. На дактилоскопическую экспертизу поступили три отпечатка фаланг пальцев рук. Вероятность непригодности к работе каждого отпечатка соответственно составляет: 0.1; 0,15; 0,2. Найти вероятность того, что все три отпечатка будут обработаны.

6. Программа экзамена содержит 40 вопросов. Студент знает 35 из них. Каждому студенту предлагают 2 вопроса, которые выбираются случайным образом. Положительная оценка ставится в том случае, если студент правильно ответил хотя бы на один вопрос. Какова вероятность успешной сдачи экзамена?

7. В неполной перетасованной колоде 10 красных карт и 8 черных. Из колоды вынимают сразу пять карт. Найти вероятность р того, что две из них будут красными, а три черными.

8. 40 экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся может ответить только на 28 вопросов. Какова вероятность того, что взятый экзаменующимся билет состоит из подготовленных им вопросов?

9. В урне 8 белых и 12 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди них будет 4 белых, а следовательно, 2 черных шара.

10. Десять различных книг расставляются наудачу на одной полке. Найти вероятность того, что 4 определенные книги окажутся поставленными рядом.

Математическая статистика

1. Проверяющий в течение контрольного периода записывал время ожидания нужного автобуса (в минутах) и получил следующие данные:

1,21	4,71	4,45	0,27	7,42	8,45	8,09	1,38
5,62	9,66	3,77	8,68	1,72	4,98	1,83	3,09
6,96	8,04	6,46	2,34	8,67	8,64	1,33	7,08
0,35	8,29	8,7	0,51	7,12	3,78	6,07	7,52
6,01	4,06	0,49	7,98	6,88	8,32	2,93	2,97

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднее время ожидания и исправленное среднее квадратическое отклонение для выборки.

2. Измерение роста 40 из прибывших новобранцев дало следующие результаты (в см):

	185,2	182,4	169,5	143,7	154,2	165,4	158,8
170,3	170,6	161,9	158,7	185,4	161,7	174,3	166,2
	179,4	162,4	160,7	177,9	169,6	149,4	171,8
176,3	176,5	171,9	153,4	172,2	182,6	169,6	159,5
177,9	165,9	156,5	163,6		171,5

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти средний рост и исправленное среднее квадратическое отклонение для выборки.

3. Агент статистической службы посетил 32 продовольственных магазина и записал цену килограмма говядины высшего сорта в каждом из них (в рублях):

200,5	194,1	200,8	211,8	211,3		189,4	198,5
194,2	201,7	197,6	184,4	198,3	206,8	210,1
198,4	201,9	194,1	202,8	188,6	206,3	214,7	201,2
210,7	198,7		199,7	183,2	185,9	194,6	199,9

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднюю цену килограмма говядины и исправленное среднее квадратическое отклонение для выборки.

4. Контролер ОТК взвесил 24 пакета кофе и записал массу каждого из них (в гр):

97,35	94,99	93,57	93,28	94,17	93,1	97,73	100,6
94,96	95,36	99,31	94,02	99,93	92,24	95,52	101,3
94,4	99,32	96,08	98,19	100,1	97,73	97,6	99,59

Построить интервальную группировку данных по пяти интервалам равной длины и соответствующую гистограмму. Найти среднюю массу пакета и исправленное среднее квадратическое отклонение для выборки.

5. Для оценки необходимых затрат рабочего времени собраны данные о том, сколько минут требуется на оформление однотипных комплектов документов случайно выбранным специалистам (в минутах):

18,24	21,82	24,39	25,04	24,23	27,43	22,53	23,2
12,23	18,89	15,74	19,01	11,16	16,53	25,89	22,69
12,22	22,59	25,38	13,95	22,29	25,34	19,87	25,73
11,45	19,09	17,89	23,05	26,44	22,04	18,52	11,08

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднюю продолжительность оформления комплекта документов и исправленное среднее квадратическое отклонение для выборки.

6. Контролер ОТК проверил срок службы 40 электрических ламп и получил следующие данные (в часах):

476,4	599,1		584,9	460,9	488,1	642,7	564,7
477,2	499,6		541,5	515,2	421,5	733,1	574,6
	406,7	468,1	473,4	461,9	545,3	558,3	427,9
526,1	403,3		515,8	410,9	503,6	594,2	554,2
558,5	498,8	449,6	453,4	500,1	486,4	509,2	574,1

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти средний срок службы лампы и исправленное среднее квадратическое отклонение для выборки.

7. Управляющий филиалом банка собрал данные о размере открытых вкладов (в тыс. руб.):

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти средний размер открываемого вклада и исправленное среднее квадратическое отклонение для выборки.

8. В продовольственном магазине в течение месяца собрана информация о числе посетителей в сутки (в тыс. человек):

0,98	1,06	1,12	1,11	0,68	1,04	0,94	0,94	0,61	1,02
0,97	1,04	0,96	1,16	1,17	0,71	0,58	1,03	0,65	1,28
1,04	0,98	0,71	0,7	1,27	1,09	1,03	0,93	1,16	1,2

Построить интервальную группировку данных по пяти интервалам равной длины и соответствующую гистограмму. Найти среднее число посетителей и исправленное среднее квадратическое отклонение для выборки.

9. Для 40 магазинов одной торговой сети, находящихся в разных населенных пунктах, определена стоимость корзины продуктов первой необходимости (в рублях):

125,2	120,2	131,3	121,6	107,8	143,8	111,5	124,8
117,3	127,5	114,6	118,2	128,7	115,6	109,1	119,8
125,9	112,3	119,6	125,7	104,4	123,9	118,1	123,7
	114,6	115,2	111,4	113,2	102,6	112,1	109,4
	114,5	109,5	125,9	120,2		114,7	109,7

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднюю стоимость корзины и исправленное среднее квадратическое отклонение для выборки.

10. В супермаркете собрана информация о времени ожидания покупателей в очереди (в мин):

3,6	1,9	2,1	0,3	0,8	0,2		1,4	1,8	1,6
1,1	1,8	0,3	1,1	0,5	1,2	0,6	1,1	0,8	1,7
1,4	0,2	1,3	3,1	0,4	2,3	1,8	4,5	0,9	0,7

Построить интервальную группировку данных по пяти интервалам равной длины и соответствующую гистограмму. Найти среднее время ожидания в очереди и исправленное среднее квадратическое отклонение для выборки.

Графы

Найдите кратчайшие маршруты, ведущие из узла А во все другие узлы сети, представленной на рисунке.