Арифметическая модель векторного пространства
Выражения вида a 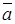 +b
+b 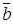 +…+g
+…+g 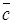 называются линейными комбинациями векторов с действительными числами.
называются линейными комбинациями векторов с действительными числами.
Теорема размерности
1.  Пусть вектор
Пусть вектор 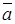 параллелен вектору
параллелен вектору  1, тогда существует xÎR такое, что
1, тогда существует xÎR такое, что 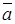 =x
=x  1.
1.
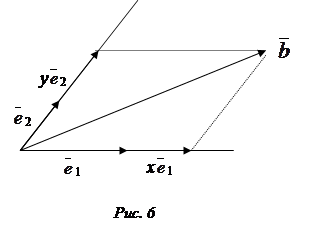
2. Пусть векторы лежат в плоскости П и  1 не параллелен
1 не параллелен  2. Тогда всякий вектор
2. Тогда всякий вектор 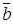 ÎП есть линейная комбинация векторов
ÎП есть линейная комбинация векторов  1 и
1 и  2:
2:
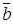 = х
= х  1 +у
1 +у  2.
2.
3. Пусть векторы  1,
1,  2 и
2 и  3 не лежат в одной плоскости. Тогда всякий вектор
3 не лежат в одной плоскости. Тогда всякий вектор 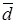 есть их линейная комбинация:
есть их линейная комбинация:
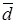 = x
= x  1 + y
1 + y  2 + z
2 + z  3
3
Доказательство проведем только для случая 2.
Выберем произвольную точку О на плоскости П и отложим из нее векторы  1,
1,  2 и
2 и 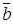 . На направления О
. На направления О  1 и О
1 и О  2 отложим направленные проекции вектора
2 отложим направленные проекции вектора 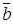 (рис. 6), обозначив их, соответственно, х
(рис. 6), обозначив их, соответственно, х  2 и у
2 и у  2. Тогда получим требуемое равенство
2. Тогда получим требуемое равенство 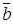 = х
= х  1 +у
1 +у  2. Случай 2 доказан. Случай 1 – тривиален, а случай 3 доказывается аналогично с построением параллелепипеда.
2. Случай 2 доказан. Случай 1 – тривиален, а случай 3 доказывается аналогично с построением параллелепипеда.
Будем говорить, что векторы  1 и
1 и  2 на рис. 6 образуют векторный базис на плоскости векторов, а числа х и у назовем координатами вектора
2 на рис. 6 образуют векторный базис на плоскости векторов, а числа х и у назовем координатами вектора 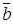 в этом базисе. Аналогично можно определить базис на прямой и в пространстве, используя случаи 1 и 3 рассмотренной теоремы.
в этом базисе. Аналогично можно определить базис на прямой и в пространстве, используя случаи 1 и 3 рассмотренной теоремы.
Таким образом, каждый вектор имеет свои координаты в заданном базисе и, наоборот, всякая тройка чисел (x,y,z) (в заданном порядке) определяет единственный вектор в этом базисе.
Вывод 1
Если в пространстве задан базис {  1,
1,  2,
2,  3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно однозначное соответствие
3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно однозначное соответствие
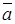 ↔(x,y,z), (1)
↔(x,y,z), (1)
определяемое разложением вектора 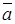 в заданном базисе:
в заданном базисе: 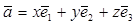 .
.
Чтобы объявить множество упорядоченных троек чисел 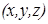 арифметической или координатной моделью трехмерного векторного пространства, покажем, что операции сложения векторов и умножения на число определены в координатной форме и, что координаты вектора определяют его длину и направление.
арифметической или координатной моделью трехмерного векторного пространства, покажем, что операции сложения векторов и умножения на число определены в координатной форме и, что координаты вектора определяют его длину и направление.
Для удобства будем считать, что 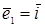 ,
, 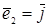 ,
, 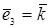 – известный в элементарной геометрии базис, состоящий из единичных взаимно перпендикулярных векторов. Для простоты также ограничимся случаем плоскости.
– известный в элементарной геометрии базис, состоящий из единичных взаимно перпендикулярных векторов. Для простоты также ограничимся случаем плоскости.
Пусть 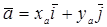 ,
, 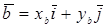 . Тогда
. Тогда 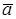 и
и 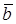 элементы геометрической модели и для них определена сумма
элементы геометрической модели и для них определена сумма
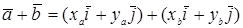 .
.
Учитываем, что 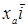 ,
, 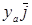 ,
, 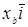 и
и 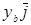 также элементы геометрической модели и, используя свойства 1–4 сложения и свойства 1–4 умножения, получаем
также элементы геометрической модели и, используя свойства 1–4 сложения и свойства 1–4 умножения, получаем

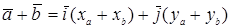
Согласно соответствию (1), установленному выше, заключаем, что 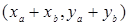 – координаты вектора
– координаты вектора 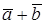 . Аналогично показывается, что вектор
. Аналогично показывается, что вектор 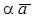 имеет координаты
имеет координаты 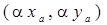 .
.
Используя теорему Пифагора, находим длину вектора на плоскости
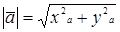
и в пространстве
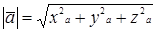 .
.
Наконец, для противоположного вектора 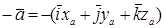 находим координаты:
находим координаты: 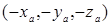 .
.
Вывод 2
Координаты 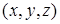 вектора
вектора 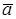 определяют его длину и направление. В координатной форме определены операции сложения векторов и умножение векторов на число. Доказательство этих фактов требует в точности восемь свойств сложения и умножения, доказанных в геометрической модели. Поэтому эти восемь свойств называют аксиомами модели векторного пространства.
определяют его длину и направление. В координатной форме определены операции сложения векторов и умножение векторов на число. Доказательство этих фактов требует в точности восемь свойств сложения и умножения, доказанных в геометрической модели. Поэтому эти восемь свойств называют аксиомами модели векторного пространства.
Мы завершили решение сформулированной в начале параграфа задачи А. Вот это решение
На множестве направленных отрезков система восьми свойств операции сложения направленных отрезков и умножения на число определяет арифметическую модель векторного пространства.
Попутно мы устанавливаем следующее свойство.
Вывод 3
Между элементами геометрической модели векторного пространства и элементами арифметической модели векторного пространства существует взаимно однозначное соответствие (1), обозначим его
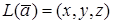 ,
, 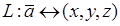 . (2)
. (2)
Это соответствие сохраняет результат линейных операций сложения векторов и умножения на число
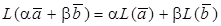 (3)
(3)
и называется изоморфизмом арифметической и геометрической моделей векторного пространства.
