II. Обращение нижней треугольной матрицы

Поступая так же, как и для обращения верхней треугольной матрицы, получаем формулы для определения элементов матрицы, которая обратна нижней треугольной матрице

В = ;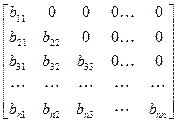

= .

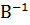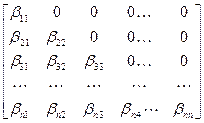При i < j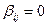

(3.7)

(т.е. все элементы, находящиеся на главной диагонали, равны нулю).

При i = j .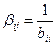

(3.8)

По этой формуле находятся диагональные элементы.

При i > j .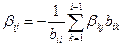

(3.9)

По этой формуле определяются элементы, находящиеся ниже главной диагонали. Из приведенных формул видно, что обратная матрица для нижней треугольной является также нижней треугольной.

Пример применения формулы (3.9). Пусть требуется определить 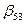(i = 5; j = 3; i > j).

;

.

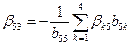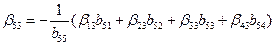В скобки заключена алгебраическая сумма произведений элементов, начиная с первого, того столбца, в котором находится определяемый элемент, на соответствующие элементы той строки матрицы В (той матрицы, для которой ищется обратная), в которой стоит определяемый элемент. Среди произведений, стоящих в скобке, могут быть и равные нулю. Это будут те произведения, у которых множитель β имеет первый индекс меньше второго.

Задача 3.2 Найти матрицу, обратную нижней треугольной матрице

= .

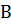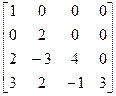Решение.Прежде всего по формуле (3.8) определяем диагональные элементы: ; ; ; .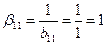

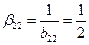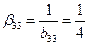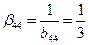Вписываем эти элементы в главную диагональ и вписываем нули на места над ней. Теперь следует определить элементы ; ; ; ; ; .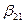

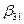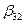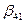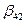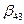Эти элементы вычислим по формуле (3.9). Для удобства помещаем матрицу 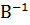под матрицей В.

= ;

=

= .

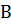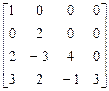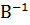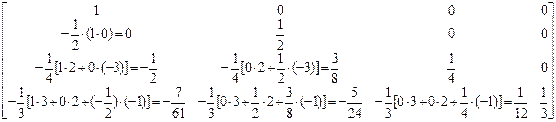
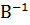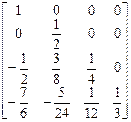III. Разложение квадратной матрицы на произведение двух треугольных

Сведения из теории.

Многие методы решения системы линейных алгебраических уравнений основаны на представлении квадратной матрицы (не треугольной) в виде произведения двух треугольных матриц, из которых одна нижняя, а другая верхняя. Для любой квадратной матрицы

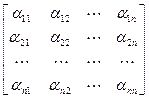
такое представление является возможным и единственным при соблюдении следующих условий:

1) диагональные элементы одной из треугольных матриц отличны от нуля;

2) главные диагональные миноры отличны от нуля (так называются миноры определителя матрицы, у которых на главных диагоналях стоят диагональные элементы матриц).

Такими минорами, например, будут:

; ; , . . .,

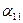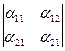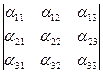а также и сам определитель матрицы .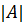

Рассмотрим такое представление на примере квадратной матрицы четвертого порядка (n = 4). Пусть требуется матрицу

А=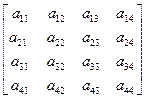

представить как произведение двух треугольных матриц (нижней и верхней)

С = 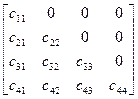и В = ,

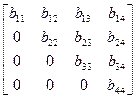т. е. предполагается, что имеется равенство

= ·

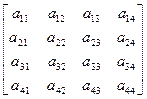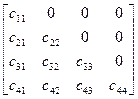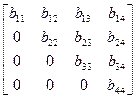(3.10)

Задача заключается в определении элементов 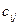(i ≥ j) и 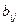(i ≤ j). Таких неизвестных элементов у нас 20, так как n² + n = 16 + 4 = 20. Это следует из формулы для суммы членов арифметической прогрессии.

Перемножим матрицы в правой части равенства (3.10) по правилу умножения матриц и, пользуясь равенством

А = CB,

приравняем элементы матрицы СВ соответствующим элементам матрицы А.

Получим такие равенства:

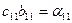		(1)	(3.11)
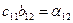		(2)
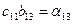		(3)
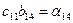		(4)
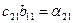		(5)
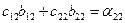		(6)
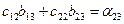		(7)
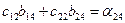		(8)
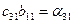		(9)
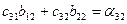		(10)
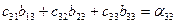		(11)
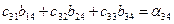		(12)
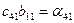		(13)
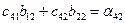		(14)
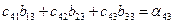		(15)
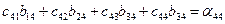		(16)

Мы получили 16 уравнений для определения 20 неизвестных. Поэтому четырем неизвестным можно приписать любое значение, причем для этого имеется бесконечное множество возможностей.

Пользуясь произвольностью выбора значений четырех неизвестных, положим, что каждый из четырех диагональных элементов в первой матрице правой части (3.10) равен единице:

; ; ; .

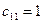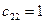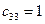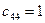Тогда первые четыре уравнения в (3.11) позволят определить неизвестные элементы 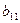, , 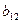, , 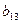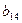и окажется, что

; ; ; .

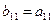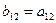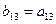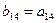(3.12)

Из уравнений (5), (9) и (13) с учетом, что 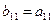, получаем:

; ; .

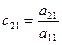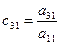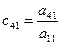(3.13)

Зная, что 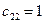, из уравнений (6), (7) и (8) находим

;

;

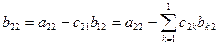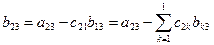(3.14)

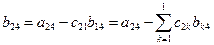
Здесь символ суммирования 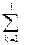, собственно, ничего нового не дает. Мы его ввели для последующих обобщений – см. формулы (3.19) и (3.20).

Замечание. Как покажут дальнейшие вычисления, суммирование производится по индексу k, который изменяется от 1 до i – 1, где i – первый индекс у определяемого элемента. В данном случае у определяемых элементов 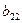, , 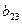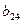первый индекс i = 2.

Из уравнений (10) и (14) находим 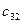и :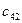

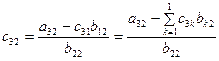;	(3.15)
.

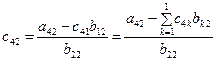В символе 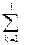индекс суммирования k изменяется от 1 до 1, т.е. фактически принимает только одно значение, равно 1, причем 1, стоящая сверху, есть 2 – 1, т.е. j – 1, где j – второй индекс у определяемых элементов 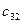и 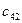. Как уже было замечено выше, введение такого символа в этом месте ничего нового не дает, но необходимо для ссылок при последующем обобщении этих формул.

Из уравнений (11) и (12) определим элементы 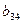и 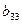(учитывая, что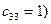

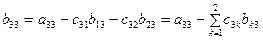;	(3.16)
.

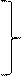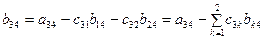В этих формулах индекс суммирования k в символе 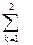изменяется от 1 до 2, а стоящее сверху этого символа число 2 = 3 – 1, т.е. i – 1, где i – первый индекс у определяемых элементов с и .

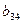Теперь из уравнения (15) найдем

.

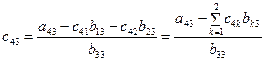(3.17)

В символе 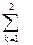индекс суммирования k изменяется от 1 до 2, причем число 2, стоящее сверху, есть j – 1, где j – второй индекс у определяемого элемента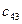

Наконец, из уравнения (16), учитывая, что 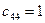, получаем

.

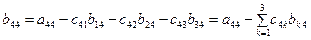(3.18)

Обратим опять внимание на то, что в символе 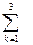индекс суммирования k изменяется от 1 до 3, причем число 3, стоящее сверху, есть 4 – 1, т.е. i – 1, где i – первый индекс у определяемого элемента .

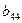Заметим, что определение элементов 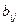и 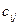чередуется: по формулам (3.12) определяются элементы 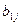(j = 1, 2, 3, 4) затем по формулам (3.13) – элементы 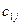(j = 1, 2, 3, 4). После этого опять определяются элементы 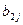(j = 2, 3, 4) по формулам (3.14), а вслед за этим по формулам (3.15) – элементы 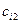(i = 3, 4), потом – опять элементы 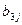(j = 3, 4) по формулам (3.16), а за ними – элементы 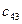по формуле (3.17) и, наконец, определяется элемент 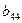по формуле (3.18).

Если объединить формулы (3.14), (3.16), (3.18) в одну, то окажется, что

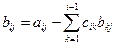; (i ≤ j)

(3.19)

(i = 2, 3, 4; j = 2, 3, 4),

а объединение формул (3.15) и (3.17) дает

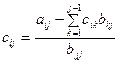; (i >j)

(3.20)

(i = 3, 4; j = 2, 3).

Формулы (3.19) и (3.20) остаются верными для представления квадратных матриц любого порядка n в виде произведения двух треугольных матриц.

Покажем схематически последовательность, в которой определяются элементы 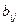и 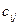: сначала заполняются строки, а потом – столбцы (см. табл. 1)

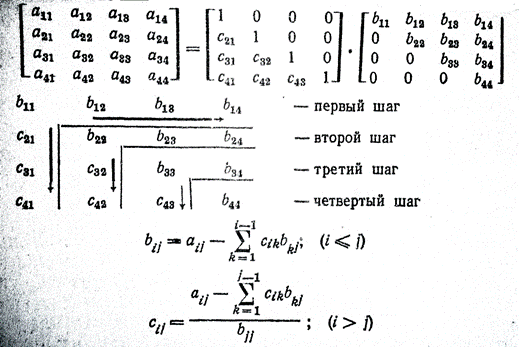Таблица 1

Представление квадратной матрицы в виде произведения нижней и верхней треугольной матрицы производится так: для удобства вычислений записывается данная матрица А, а под ней – матрицы С и В, как указано в табл. 2, на следующей странице, причем вместо диагональных элементов матрицы С вписываются единицы.

Первая строка матрицы В и первый столбец матрицы С заполняются так, как указано в табл. 2 (см. след. стр.):

1. На основании формул (3.12) в первую строку вписываются соответствующие элементы матрицы А, а элементы первого столбца матрицы С равны соответствующим элементам первого столбца матрицы А, разделенным на его первый элемент – формулы (3.13).

2. Элементы, стоящие над ступенчатой линией, находятся по формуле (3.19) так: берется соответствующий элемент матрицы А и из него вычитаются произведения элементов, стоящих в той же строке левее и в том же столбце выше, что и вычисляемый элемент, причем первый элемент строки умножается на первый элемент столбца, второй элемент строки – на второй элемент столбца и т.д.

Таблица 2

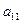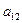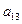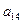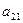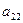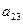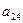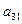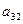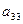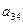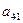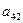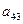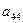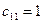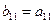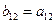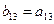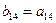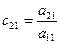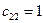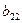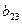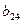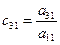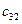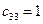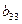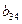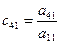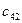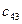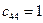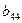3. При вычислении же элементов, расположенных под ступенчатой линией, поступают так же, как в п. 2, но полученный результат делят на диагональный элемент 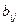(j = 2, 3), стоящий в том столбце (формула (3.20), что и определяемый элемент.

Этот алгоритм вычисления элементов двух треугольных матриц – нижней и верхней, на которые разлагается матрица А, легко распространяется на квадратные матрицы любого порядка.

Задача 3.3

Матрицу

=

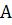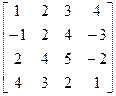
представить в виде произведения нижней и верхней треугольных матриц.

Решение.Используем только что указанный порядок действий и расположим действия, как в табл. 2, причем приведем подробно все выкладки в каждой клетке и будем придерживаться порядка заполнения клеток, указанного в табл.1 (см. выше):

-1			-3
			-2

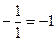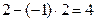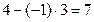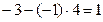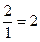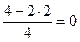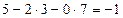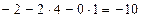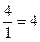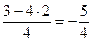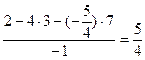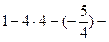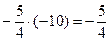Итак, нижняя треугольная матрица

= ,

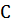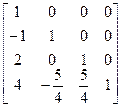а верхняя треугольная матрица

В = .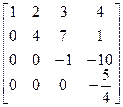

Легко проверить, что

СВ = А

Задача 3.4 При определении неизвестных элементов 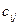и 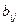мы приняли, что 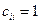(i = 1, 2, 3, 4). Покажем, что если взять 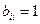(i = 1, 2, 3, 4), то неизвестные элементы 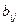и 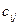матриц, стоящих в правой части формулы (3.10), определяются по следующим формулам: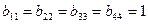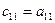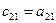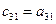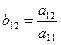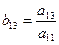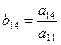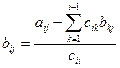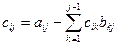

; ; , … ; ; ; , если (i < j) , если (i ≥ j)

(3.21)

Указание. В этом случае матрица А представляется в виде произведения таких двух треугольных матриц (нижней и верхней):

= × .

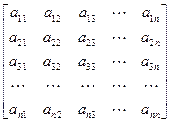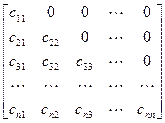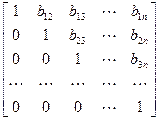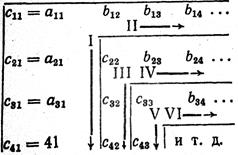Последовательность определения элементов 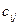(i ≥ j) и 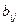(i < j) указывается такой схемой:

(Римские цифры над стрелками указывают последовательность, в которой должны определятся элементы).

Задача 3.5 Пользуясь формулами (3.21), представить матрицу

=

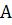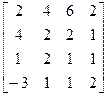
в виде произведения двух треугольных матриц нижней и верхней.

Решение.Поступим так же, как и в предыдущем случае. Напишем матрицу А, а под ней матрицы С и В – см. формулу (3.10), причем вместо диагональных элементов матрицы впишем 1. В нижней таблице подробно выполнены все вычисления по формулам (3.21).

-3
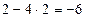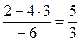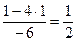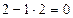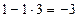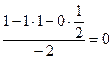-3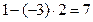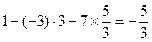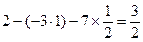

Таким образом, матрица А представлена в виде произведения

= · .

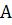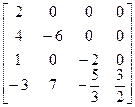Замечание. Во всех предыдущих вычислениях мы представляли матрицу в виде произведения двух треугольных: первый сомножитель был нижней, а второй – верхней треугольной матрицы. Однако такой порядок сомножителей не является обязательным и матрицу можно разложить на произведение двух треугольных матриц так, чтобы первый сомножитель был верхней, а второй – нижней треугольной матрицей. Относящиеся к этому случаю формулы мы указывать не будем.