Обращение матрицы nхn с использованием метода Гаусса
По определению, обратная матрица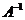 
матрицы A размерности n*n должна удовлетворять соотношению:
A×A-1=E (6)
Уравнение (6) представляет собой систему n систем линейных уравнений вида:
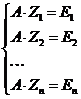(7)
Здесь Z1, Z2,… Zn – столбцы искомой обратной матрицы, E1=(1,0,0,…,0), E2=(0,1,0,…,0), …En=(0,0,…,1) – соответствующие столбцы единичной матрицы.
Решая n систем линейных уравнений (7) получаем столбцы обратной матрицы A.
Находить решение систем линейных уравнений (7) можно любым подходящим численным методом. Основной принцип метода Гаусса – приведение матрицы к треугольному виду – может быть использован для решения задачи нахождения обратной матрицы n*n элементов. Если в методе Гаусса, при каждом проходе по строкам системы в качестве правой части использовать вектор с единственным единичным элементом, соответствующим текущей обрабатываемой строке, то получим алгоритм обращения матрицы n*n с использованием метода Гаусса.
Описание алгоритма вычисления обратной матрицы n*n методом Гаусса:
Задаем коэффициенты исходной системы линейных уравнений a(n,n) и правые части b(n).
Задаем цикл по j от 1 до n.
Задаем цикл по k от 1 до n.
В цикле по k зануляем все значения правой части системы b(k)=0.
Конец цикла по k.
В цикле по j:
Задаем значение для текущего уравнения j значение правой части уравнения равное 1 (b(j)=1).
По имеющейся системе уравнений с помощью метода Гаусса вычисляем решения системы x(1..n).
Задаем цикл по k от 1 до n.
Копируем в цикле по k только что найденные значения x(k=1….k=n) в j-й столбец временной матрицы с(n,n).
Конец цикла по k.
Конец цикла по j.
Задаем цикл по i от 1 до n.
Задаем цикл по j от 1 до n.
В цикле по j копируем найденные значения обратной матрицы, содержащиеся во временной матрице с(n,n), в матрицу a(n,n).
Конец цикла по j.
Конец цикла по i.
Конец алгоритма.
Пример алгоритма вычисления обратной матрицы n×n методом Гаусса на естественном языке:
lb=нижняя_граница_диапазона_случайных_чисел
ub=верхняя_граница_диапазона_случайных_чисел
dec=количество_знаков_после_запятой
n=размерность_системы
Определить Массив a(n,n),x(n),b(n)
* формируем матрицу коэффициентов уравнения и выводим их на печать
Печать " Матрица коэффициентов a(n,n)"
Вызвать Случ_Матирица(@a,n,lb,ub,dec,1)
* формируем правую часть системы и выводим ее на печать
Печать" Правые частии системы b(n)"
Вызвать Случ_Вектор(@b,n,lb,ub,dec,1)
* "Выводим коэффициенты исходной системы"
Вызвать Печать_Системы(@a,@b,n,dec)
* "Находим обратную матрицу методом Гаусса"
Вызвать Обратить_Матрицу(@a,n)
* "Выводим обратную матрицу"
Вызвать Печать_Системы(@a,@b,n,dec)
Печать" Конец программы "
Определить Процедуру Обратить_Матрицу
Параметры a,n
Определить Локальный Массив c(n,n),b(n),x(n)
Определить Локальную Переменную i,j,k,l,m
Цикл по j от 1 до n
Цикл по k от 1 до n
b(k)=0
Конец Цикла
b(j)=1
Вызвать Метод_Гаусса(@a,@b,@x,n)
FOR k=1 TO n
c(k,j)=x(k)
Конец Цикла
Конец Цикла
Цикл по i от 1 до n
Цикл по j от 1 до n
a(i,j)=c(i,j)
Конец Цикла
Конец Цикла
Конец Определения Процедуры
Определить Функцию Случ_Матирица
Параметры a,n,lb,ub,dec,prnt
Определить Массив a(n,n)
Цикл по i от 1 до n
Цикл по j от 1 до n
a(i,j)=(ub-lb)*Случайный()+lb
a(i,j)=Округлить(a(i,j),dec)
Конец Цикла
Конец Цикла
Если prnt=1 Тогда
Цикл по i от 1 до n
Цикл по j от 1 до n
Печать a(i,j)
Конец Цикла
Печать
Конец Цикла
Конец Если
Возврат
Конец Определения Функции
Определить Функцию Случ_Вектор
Параметры a,n,lb,ub,dec,prnt
Определить Массив a(n)
Цикл по i от 1 до n
a(i)=(ub-lb)*Случайный()+lb
a(i)=Округлить(a(i),dec)
Конец Цикла
Если prnt=1 Тогда
Цикл по i от 1 до n
Печать a(i)
Конец Цикла
Конец Если
Конец Определения Функции
Определить Функцию Метод_Гаусса
Параметры a_tmp,b,x,n
Определить локальный Массив a(n,n)
Цикл по j от 1 до n
Цикл по i от 1 до n
a(i,j)=a_tmp(i,j)
Конец Цикла
Конец Цикла
* приводим к треугольному виду
Цикл по k от 1 до n-1
Цикл по l от k+1 до n
p=a(l,k)/a(k,k)
Цикл по m от k до n
a(l,m)=a(l,m)-a(k,m)*p
Конец Цикла
b(l)=b(l)-b(k)*p
Конец Цикла
Конец Цикла
* вычисляем x
Цикл по k от n до 1 с шагом -1
s=0
Цикл по l от k+1 до n
s=s+a(k,l)*x(l)
Конец Цикла
x(k)=(b(k)-s)/a(k,k)
Конец Цикла
Возврат
Конец Определения Функции
Определить Функцию Печать_Системы
Параметры a,b,n,dec
Цикл по i от 1 до n
Цикл по j от 1 до n
Печать a(i,j)
Конец Цикла
Печать " :" + b(i)
Конец Цикла
Возврат
Конец Определения Функции
Пример реализации алгоритма вычисления обратной матрицы NxN методом Гаусса на VFP:
CLEAR
lb=-0.5
ub=0.5
dec=6
n=3
DIMENSION a(n,n),x(n),b(n)
* формируем матрицу коэффициентов уравнения и выводим их на печать
? " Матрица коэффициентов a(n,n)"
CreateRNDMartix(@a,n,lb,ub,dec,1)
?
* формируем правую часть системы и выводим ее на печать
?" Правые частии системы b(n)"
CreateRNDVector(@b,n,lb,ub,dec,1)
?
* "Выводим коэффициенты исходной системы"
PrintSystem(@a,@b,n,dec)
* "Находим обратную матрицу методом Гаусса"
Reverse_Matrix(@a,n)
?
* "Выводим обратную матрицу"
PrintSystem(@a,@b,n,dec)
?
?" Конец программы !!!"
PROCEDURE Reverse_Matrix
LPARAMETERS a,n
LOCAL ARRAY c(n,n),b(n),x(n)
LOCAL i,j,k,l,m
FOR j=1 TO n
FOR k=1 TO n
b(k)=0
ENDFOR
b(j)=1
Gauss_Classic(@a,@b,@x,n)
FOR k=1 TO n
c(k,j)=x(k)
ENDFOR
ENDFOR
FOR i=1 TO n
FOR j=1 TO n
a(i,j)=c(i,j)
ENDFOR
ENDFOR
ENDPROC
FUNCTION CreateRNDMartix
LPARAMETERS a,n,lb,ub,dec,prnt
FOR i=1 TO n
FOR j=1 TO n
a(i,j)=(ub-lb)*RAND()+lb
a(i,j)=ROUND(a(i,j),dec)
ENDFOR
ENDFOR
IF prnt=1 then
?
FOR i=1 TO n
FOR j=1 TO n
?? a(i,j)
ENDFOR
?
ENDFOR
ENDIF
RETURN
ENDFUNC
FUNCTION CreateRNDVector
LPARAMETERS a,n,lb,ub,dec,prnt
FOR i=1 TO n
a(i)=(ub-lb)*RAND()+lb
a(i)=ROUND(a(i),dec)
ENDFOR
IF prnt=1 then
FOR i=1 TO n
? a(i)
ENDFOR
ENDIF
ENDFUNC
FUNCTION Gauss_Classic
LPARAMETERS a_tmp,b,x,n
LOCAL ARRAY a(n,n)
FOR j=1 TO n
FOR i=1 TO n
a(i,j)=a_tmp(i,j)
ENDFOR
ENDFOR
* приводим к треугольному виду
FOR k=1 TO n-1
FOR l=k+1 TO n
p=a(l,k)/a(k,k)
FOR m=k TO n
a(l,m)=a(l,m)-a(k,m)*p
ENDFOR
b(l)=b(l)-b(k)*p
ENDFOR
ENDFOR
* вычисляем x
FOR k=n TO 1 STEP -1
s=0
FOR l=k+1 TO n
s=s+a(k,l)*x(l)
ENDFOR
x(k)=(b(k)-s)/a(k,k)
ENDFOR
RETURN
ENDFUNC
FUNCTION PrintSystem
LPARAMETERS a,b,n,dec
FOR i=1 TO n
?
FOR j=1 TO n
?? STR(a(i,j),dec*2+2,dec)
ENDFOR
?? " :" + STR(b(i),dec*2+2,dec)
ENDFOR
RETURN
ENDFUNC
В данной реализация использован прием формирования матрицы коэффициентов системы уравнений случайным образом из заданного диапазона, при этом границы диапазона определяются значениями lb (low bound – нижняя граница) и ub (upper bound – верхняя граница).
Запись Округлить() и Случайный() означают соответственно вызовы стандартных встроенных функций округления и возврата псевдослучайного значения из диапазона от 0 до 1.
Пример реализации алгоритма вычисления обратной матрицы nxn методом Гаусса на VBA:
Sub Find_Reverse_Matrix()
Dim a(), b(), x()
n = 3
dec = 4
ReDim a(n, n): ReDim b(n): ReDim x(n)
Call Read_Matrix("C:\Temp\system.txt", a(), b(), n)
' Выводим на экран исходную систему
Call Print_Matrix(a(), b(), n, dec)
' Вычисляем обратную матрицу методом Гаусса
Call Reverse_Matrix(a(), b(), x(), n)
' "Выводим обратную матрицу"
Call Print_Matrix(a(), b(), n, dec)
MsgBox "Конец программы !!!"
End Sub
Sub Reverse_Matrix(a(), b(), x(), n)
Dim i, j, k, l, m
Dim c()
ReDim c(n, n)
For j = 1 To n
For k = 1 To n
b(k) = 0
Next k
b(j) = 1
Call Gauss_Classic(a(), b(), x(), n)
For k = 1 To n
c(k, j) = x(k)
Next k
Next j
For i = 1 To n
For j = 1 To n
a(i, j) = c(i, j)
Next j
Next i
End Sub
Sub Gauss_Classic(a_tmp(), b(), x(), n)
Dim i, j, k, l, m
Dim a()
Redim a(n,n)
a()=a_tmp()
' приводим к треугольному виду
For k = 1 To n - 1
For l = k + 1 To n
p = a(l, k) / a(k, k)
For m = k To n
a(l, m) = a(l, m) - a(k, m) * p
Next m
b(l) = b(l) - b(k) * p
Next l
Next k
' вычисляем x
For k = n To 1 Step -1
s = 0
For l = k + 1 To n
s = s + a(k, l) * x(l)
Next l
x(k) = (b(k) - s) / a(k, k)
Next k
End Sub
Sub Read_Matrix(file_path, a(), b(), n)
Dim s, s1, i, j
nf = FreeFile
Open file_path For Input As #nf
For i = 1 To n
pos1 = 1
Input #nf, s
For j = 1 To n
pos2 = InStr(pos1, s, ";")
s1 = Mid(s, pos1, pos2 - pos1)
a(i, j) = Val(s1)
pos1 = pos2 + 1
Next j
pos2 = InStr(pos1, s, ";")
s1 = Mid(s, pos1, pos2 - pos1)
b(i) = Val(s1)
Next i
Close #nf
End Sub
Sub Print_Matrix(a(), b(), n, dec)
Dim i
Dim DStr, str
DStr = "0."
For i = 1 To dec
DStr = DStr + "0"
Next i
str = ""
For i = 1 To n
str = str & vbCrLf
For j = 1 To n
str = str & Format(a(i, j), DStr) & " : "
Next j
str = str & " : " & Format(b(i), DStr)
Next i
Debug.Print str
End Sub
Данная реализация алгоритма использует чтение коэффициентов системы уравнений из текстового файла. Текстовый файл, например, для системы с тремя уравнениями, должен быть следующего вида:
"0.34;0.71;0.63;2.08;"
"0.71;-0.36;-0.18;0.17;"
"1.17;-2.35;0.75;1.28;"
т.е. в каждой строке файла записываются коэффициенты первой строки системы (i=1, a(i,j), b(i)), при этом вся строка заключена в кавычки (т.е. рассматривается VBA как текстовая строка) и после каждого коэффициента ставиться разделитель – точка с запятой (;).
Контрольные вопросы
1. Что такое система линейных уравнений?
2. Что такое решение системы линейных уравнений?
3. Что такое совместность и полнота системы линейных уравнений?
4. Что такое вырожденная система линейных уравнений?
5. Что такое определитель матрицы системы линейных уравнений?
6. Что такое однородная система линейных уравнений?
7. Что такое собственные значения матрицы?
8. Что такое характеристическая функция системы линейных уравнений?
9. Привести алгоритм табуляции характеристической функции системы линейных уравнений.
10. Как найти собственный вектор системы линейных уравнений?
11. Как найти ненулевое решение однородной системы линейных алгебраических уравнений?
12. Привести алгоритм решения системы линейных уравнений методом простой итерации.
13. В чем состоит условие сходимости метода простой итерации для системы линейных уравнений?
14. Как определить точность вычисления решений системы линейных уравнений методом простой итерации?
15. Привести алгоритмы вычисления разностей векторов и длин разностей векторов (норм).
16. Привести алгоритм определения степени сходимости метода простой итерации для системы линейных уравнений.
17. Привести алгоритм модифицированного (с параметром, улучшающим сходимость) метода простой итерации для системы линейных уравнений.
18. Привести алгоритм метода Гаусса-Зейделя.
19. Привести алгоритм обращения матрицы nxn.
Задания
Методами Зейделя и Гаусса-Зейделя решить с точностью до 0,001 систему линейных уравнений. Численным методом найти обратные матрицы к матрицам коэффициентов систем линейных уравнений. Матрицы коэффициентов и векторы правых частей считывать из:
а) текстовых файлов;
б) dbf-таблицы;
в) MS’Excel;
г) MS’Word.
| №1 | 2,7x1+3,3x2+1,3x3=2,1; 3,5x1–1,7x2+2,8x3=1,7; 4,1x1+5,8x2–1,7x3=0,8. | №2 | 1,7x1+2,8x2+1,9x3=0,7; 2,1x1+3,4x2+1,8x3=1,1; 4,2x1–1,7x2+1,3x3=2,8. |
| №3. | 3,1x1+2,8x2+1,9x3=0,2; 1,9x1+3,1x2+2,1x3=2,1; 7,5x1+3,8x2+4,8x3=5,6. | №4. | 9,1x1+5,6x2+7,8x3=9,8; 3,8x1+5,1x2+2,8x3=6,7; 4,1x1+5,7x2+1,2x3=5,8. |
| №5. | 3,3x1+2,1x2+2,8x3=0,8; 4,1x1+3,7x2+4,8x3=5,7; 2,7x1+1,8x2+1,1x3=3,2. | №6. | 7,6x1+5,8x2+4,7x3=10,1; 3,8x1+4,1x2+2,7x3=9,7; 2,9x1+2,1x2+3,8x3=7,8. |
| №7. | 3,2x1–2,5x2+3,7x3=6,5; 0,5x1+0, 34x2+1,7x3=0,24; 1,6x1+2,3x2–1,5x3=4,3. | №8. | 5,4x1–2,3x2+3,4x3= –3,5; 4,2x1+1,7x2–2,3x3=2,7; 3,4x1+2,4x2+7,4x3=1,9. |
| №9. | 3,6x1+1,8x2–4,7x3=3,8; 2,7x1–3,6x2+1,9x3=0,4; 1,5x1+4,5x2+3,3x3= –1,6. | №10. | 5,6x1+2,7x2–1,7x3=1,9; 3,4x1–3,6x2–6,7x3= –2,4; 0,8x1+1,3x2+3,7x3=1,2. |
| №11. | 2,7x1+0,9x2–1,5x3=3,5; 4,5x1–2,8x2+6,7x3=2,6; 5,1x1+3,7x2–1,4x3= –0,14. | №12. | 4,5x1–3,5x2+7,4x3=2,5; 3,1x1–0,6x2–2,3x3= –1,5; 0,8x1+7,4x2–0,5x3=6,4. |
| №13. | 3,8x1+6,7x2–1,2x3=5,2; 6,4x1+1,3x2–2,7x3=3,8; 2,4x1–4,5x2+3,5x3= –0,6. | №14. | 5,4x1–6,2x2–0,5x3=0,52; 3,4x1+2,3x2+0,8x3= –0,8; 2,4x1–1,1x2+3,8x3=1,8. |
| №15. | 7,8x1+5,4x2+4,8x3=1,8; 3,3x1+1,1x2+1,8x3=2,3; 4,5x1+3,3x2+2,8x3=3,4. | №16. | 3,8x1+4,1x2–2,3x3=4,8; –2,1x1+3,9x2–5,8x3=3,3; 1,8x1+1,1x2–2,1x3=5,8. |
| №17. | 1,7x1–2,2x2+3,0x3=1,8; 2,1x1+1,9x2–2,3x3=2,8; 4,2x1+3,9x2–3,1x3=5,1. | №18. | 2,8x1+3,8x2–3,2x3=4,5; 2,5x1–2,8x2+3,3x3=7,1; 6,5x1–7,1x2+4,8x3=6,3. |
| №19. | 3,3x1+3,7x2+4,2x3=5,8; 2,7x1+2,3x2–2,9x3=6,1; 4,1x1+4,8x2–5,0x3=7,0. | №20. | 7,1x1+6,8x2+6,1x3=7,0; 5,0x1+4,8x2+5,3x3=6,1; 8,2x1+7,8x2+7,1x3=5,8. |
| №21. | 3,7x1+3,1x2+4,0x3=5,0; 4,1x1+4,5x2–4,8x3=4,9; –2,1x1–3,7x2+1,8x3=2,7. | №22. | 4,1x1+5,2x2–5,8x3=7,0; 3,8x1–3,1x2+4,0x3=5,3; 7,8x1+5,3x2–6,3x3=5,8. |
| №23. | 3,7x1–2,3x2+4,5x3=2,4; 2,5x1+4,7x2–7,8x3=3,5; 1,6x1+5,3x2+1,3x3= –2,4. | №24. | 6,3x1+5,2x2–0,6x3=1,5; 3,4x1–2,3x2+3,4x3=2,7; 0,8x1+1,4x2+3,5x3= –2,3. |