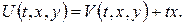Винятком тут знову є друга змішана задача. крайова задача
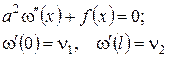
має розв’язок, якщо виконується умова 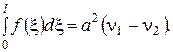 Якщо ж ця умова не виконується, то задану другу змішану задачу слід інтеґрувати як задачу типу 2 при
Якщо ж ця умова не виконується, то задану другу змішану задачу слід інтеґрувати як задачу типу 2 при 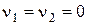 , або як загальну змішану задачу у випадку неоднорідних крайових умов.
, або як загальну змішану задачу у випадку неоднорідних крайових умов.
- 9 -
ПРИКЛАД 1. Проінтеґрувати змішану задачу та дати фізичну інтерпретацію:
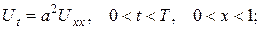 (3)
(3)
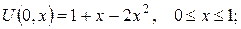 (4)
(4)
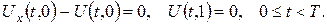 (5)
(5)
Фізична інтерпретація:знайти закон зміни температури в однорідному ізотропному стержні одиничної довжини з теплоізольованою бічною поверхнею, якщо початкова температура точок стержня рівна 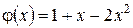 , на правому кінці підтримується нульова температура, а на лівому відбувається теплообмін по закону Ньютона з навколишнім середовищем нульової температури.
, на правому кінці підтримується нульова температура, а на лівому відбувається теплообмін по закону Ньютона з навколишнім середовищем нульової температури.
Розв’язання. Рівняння та крайові умови однорідні (задача типу 1). Початкова та крайові умови узгоджені, отже, можемо застосувати метод відокремлення змінних. Розв’язок шукаємо у вигляді добутку:
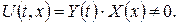 (6)
(6)
Підставивши (6) у рівняння (3) та крайові умови (5), одержимо:
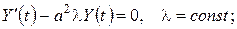 (7)
(7)
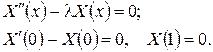 (8)
(8)
Дослідимо задачу Штурма-Ліувілля (8).
1. Нехай 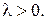 Тоді загальний розв’язок рівняння з (8) запишеться у вигляді
Тоді загальний розв’язок рівняння з (8) запишеться у вигляді 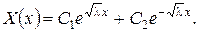 Підставивши цей розв’язок у крайові умови, одержимо лінійну однорідну систему відносно невідомих сталих С1 і С2:
Підставивши цей розв’язок у крайові умови, одержимо лінійну однорідну систему відносно невідомих сталих С1 і С2:
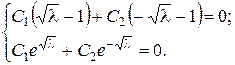
Детермінант цієї системи 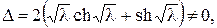 поскільки
поскільки 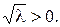 Отже,
Отже, 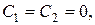 а тому
а тому 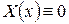 і
і 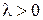 не є власним значенням.
не є власним значенням.
2. Нехай 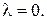 Тоді
Тоді 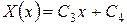 і з крайових умов одержимо:
і з крайових умов одержимо:
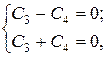
звідки 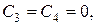 а тому
а тому 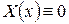 і
і 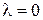 також не є власним значенням.
також не є власним значенням.
3. При 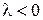 загальний розв’язок рівняння з (8) запишеться у вигляді
загальний розв’язок рівняння з (8) запишеться у вигляді 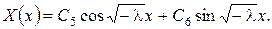 Із крайових умов одержимо:
Із крайових умов одержимо:
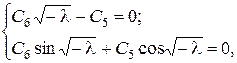
- 10 -
звідки 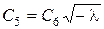 і
і 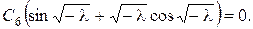 Отже, нетривіальний розв’язок задачі (8) існує тільки для тих значень параметру λ, які є розв’язками трансцендентного рівняння
Отже, нетривіальний розв’язок задачі (8) існує тільки для тих значень параметру λ, які є розв’язками трансцендентного рівняння 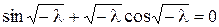 або
або
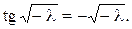 (9)
(9)
Рівняння (9) має счисленну множину коренів 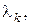
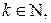 причому всі корені є дійсними. Введемо позначення
причому всі корені є дійсними. Введемо позначення 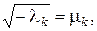
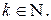 Тоді відповідні власні функції матимуть вигляд (беремо для визначеності С6=1)
Тоді відповідні власні функції матимуть вигляд (беремо для визначеності С6=1)
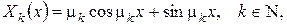
де 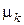 – додатні корені рівняння
– додатні корені рівняння 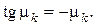
Підставивши знайдені власні значення 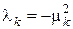 у рівняння (7) та проінтеґрувавши його, одержимо:
у рівняння (7) та проінтеґрувавши його, одержимо:
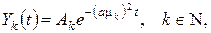
де 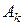 – довільні сталі. Тоді згідно (6) будь-який частинний розв’язок рівняння (3), який справджує крайові умови (5), запишеться у вигляді
– довільні сталі. Тоді згідно (6) будь-який частинний розв’язок рівняння (3), який справджує крайові умови (5), запишеться у вигляді
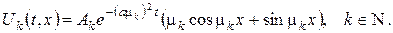
В силу лінійності й однорідності рівняння (3) сума частинних розв’язків
 (10)
(10)
також буде розв’язком рівняння (3) і справджуватиме крайові умови (5). Сталі 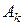 визначаємо підстановкою ряду (10) у початкову умову (4). Маємо:
визначаємо підстановкою ряду (10) у початкову умову (4). Маємо:
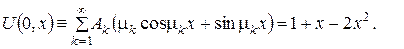
Домножимо на 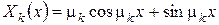 ліву і праву частини останньої рівності і проінтеґруємо по змінній х на проміжку [0;1]. Тоді, врахувавши властивість ортоґональності власних функцій, які відповідають різним власним значенням, одержимо:
ліву і праву частини останньої рівності і проінтеґруємо по змінній х на проміжку [0;1]. Тоді, врахувавши властивість ортоґональності власних функцій, які відповідають різним власним значенням, одержимо:
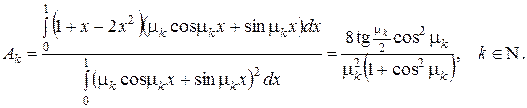
Підставивши знайдені коефіцієнти в ряд (10), одержимо розв’язок змішаної задачі (3)-(5).
ПРИКЛАД 2. Знайти закон зміни температури всередині однорідного ізотропного стержня довжини 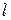 з теплоізольованою бічною поверхнею, якщо в лівому кінці стержня температура змінюється згідно закону
з теплоізольованою бічною поверхнею, якщо в лівому кінці стержня температура змінюється згідно закону 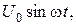 де
де 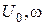 задані сталі, а в правому підтримується нульова температура. Всередині
задані сталі, а в правому підтримується нульова температура. Всередині
- 11 -
стержня є джерела та поглиначі тепла: їх інтенсивність (в розрахунку на одиницю маси стержня) рівна 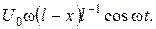 Початкова температура точок стержня задана функцією
Початкова температура точок стержня задана функцією 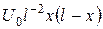 .
.
Розв’язання. Математична модель задачі:
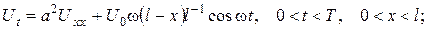
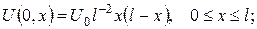
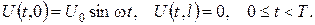
Крайові умови неоднорідні (задача типу 3), тому для застосування методу Фур’є спершу слід звести вихідну задачу до задачі з однорідними крайовими умовами. Покладемо 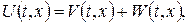 де
де 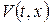 – нова невідома функція, а
– нова невідома функція, а 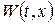 – допоміжна функція, котра справджує неоднорідні крайові умови. Згідно викладеного вище
– допоміжна функція, котра справджує неоднорідні крайові умови. Згідно викладеного вище
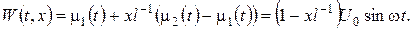
Тоді для знаходження функції 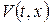 одержимо змішану задачу
одержимо змішану задачу
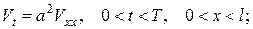
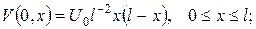
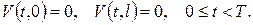
Початкова та крайові умови є узгодженими, отже, до одержаної задачі застосовний метод Фур’є. Шукаючи розв’язок аналоґічно до прикладу 1, знаходимо
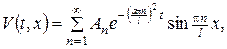
де
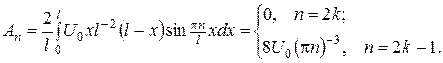
Отже,
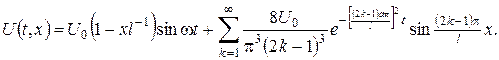
ПРИКЛАД 3.Знайти розподіл температури в однорідній ізотропній кулі радіуса 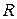 із центром у початку координат, якщо в початковий момент часу температура кулі була рівна
із центром у початку координат, якщо в початковий момент часу температура кулі була рівна 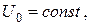 на поверхні кулі підтримується температура
на поверхні кулі підтримується температура 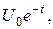 а всередині кулі діють поглиначі тепла інтенсивності
а всередині кулі діють поглиначі тепла інтенсивності 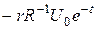 ,
, 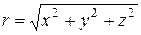 .
.
Розв’язання. Для запису математичної моделі задачі необхідно перейти до сферичних координат 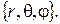 Але, поскільки вихідні дані в умові задачі не
Але, поскільки вихідні дані в умові задачі не
- 12 -
залежать від кутів θ та φ, то в силу симетричності кулі будемо мати 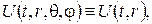 тобто для довільного фіксованого
тобто для довільного фіксованого 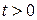 температура точок кулі залежатиме тільки від відстані до центра кулі (радіальний розподіл). Врахувавши це, запишемо математичну модель задачі:
температура точок кулі залежатиме тільки від відстані до центра кулі (радіальний розподіл). Врахувавши це, запишемо математичну модель задачі:
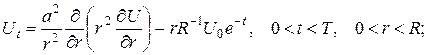
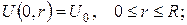
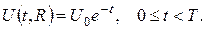
Перейдемо до нової невідомої функції 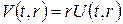 (стандартна підстановка в задачах на радіальний розподіл температури в кулі). Одержимо наступну змішану задачу:
(стандартна підстановка в задачах на радіальний розподіл температури в кулі). Одержимо наступну змішану задачу:
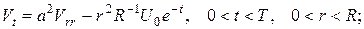
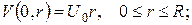
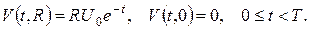
Остання крайова умова є наслідком обмеженості температури в центрі кулі. Справді, поскільки всі вихідні дані в умові задачі є обмеженими функціями в розглядуваній області, то 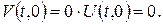
Крайові умови неоднорідні, отже, маємо задачу типу 3 (загальна змішана задача). Тому розв’язок шукаємо у вигляді 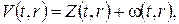 причому для
причому для 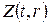 крайові умови повинні бути однорідними, отже, допоміжна функція
крайові умови повинні бути однорідними, отже, допоміжна функція 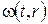 повинна справджувати умови
повинна справджувати умови
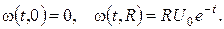
Шукаємо допоміжну функцію у вигляді 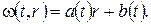 Із крайових умов одержуємо:
Із крайових умов одержуємо: 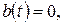
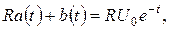 звідки
звідки 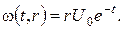
Підставивши 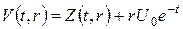 у змішану задачу для
у змішану задачу для 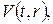 одержимо змішану задачу для нової невідомої функції
одержимо змішану задачу для нової невідомої функції 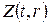 :
:
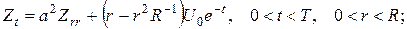 (11)
(11)
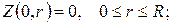 (12)
(12)
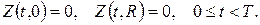
Це задача для неоднорідного рівняння з однорідними крайовими умовами (задача типу 2), до якої застосовний метод Фур’є, поскільки вільний член у рівнянні справджує крайові умови по змінній 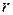 . Розв’язування такої задачі проводиться у два етапи.
. Розв’язування такої задачі проводиться у два етапи.
Перший етап. Для відповідної однорідної задачі
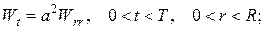
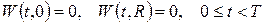
- 13 -
класичним методом відокремлення змінних 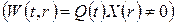 знаходимо власні функції відповідної задачі Штурма-Ліувілля (початкову умову тут поки що не враховуємо). Одержимо:
знаходимо власні функції відповідної задачі Штурма-Ліувілля (початкову умову тут поки що не враховуємо). Одержимо:
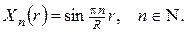
Другий етап. Функцію 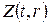 шукаємо у вигляді ряду по системі знайдених власних функцій:
шукаємо у вигляді ряду по системі знайдених власних функцій:
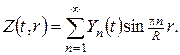 (13)
(13)
Для визначення функцій 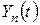 підставимо ряд (13) у рівняння (11) та в початкову умову (12). Одержимо:
підставимо ряд (13) у рівняння (11) та в початкову умову (12). Одержимо:
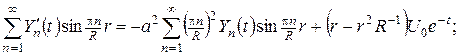
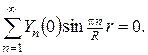
Звідси
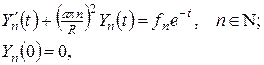 (14)
(14)
де коефіцієнт Фур’є
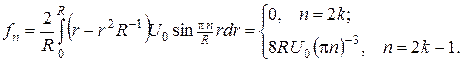
Розв’язками задач Коші (14) будуть функції
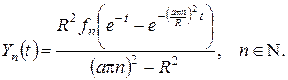 (15)
(15)
Підставивши (15) у ряд (13), одержимо функцію 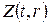 . А тоді
. А тоді
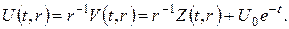
ПРИКЛАД 4. Знайти закон зміни температури в однорідному (а=1) ізотропному стержні довжини 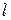 , лівий кінець якого теплоізольований, а до правого підводиться сталий тепловий потік
, лівий кінець якого теплоізольований, а до правого підводиться сталий тепловий потік 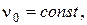 якщо початкова температура точок стержня задана функцією
якщо початкова температура точок стержня задана функцією 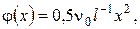 а через бічну поверхню стержня проходить теплообмін (із коефіцієнтом b=1) з навколишнім середовищем нульової температури.
а через бічну поверхню стержня проходить теплообмін (із коефіцієнтом b=1) з навколишнім середовищем нульової температури.
Розв’язання. 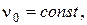 отже, маємо задачу типу 4 (задача зі стаціонарними неоднорідностями):
отже, маємо задачу типу 4 (задача зі стаціонарними неоднорідностями):
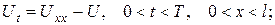
- 14 -
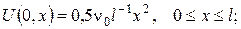
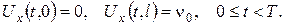
Розв’язок будемо шукати у вигляді 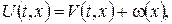 де стаціонарна температура
де стаціонарна температура 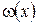 визначається з крайової задачі
визначається з крайової задачі
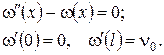
Проінтеґрувавши крайову задачу, одержимо 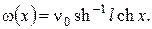 Тоді після заміни
Тоді після заміни 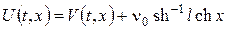 для нової невідомої функції
для нової невідомої функції 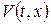 одержимо змішану задачу
одержимо змішану задачу
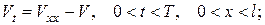
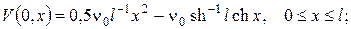
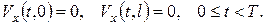
Поскільки крайові умови однорідні, то для спрощення рівняння зручно ввести підстановку 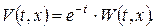 Тоді для
Тоді для 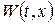 матимемо задачу
матимемо задачу
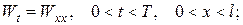
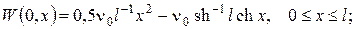
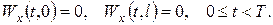
Розв’язок одержаної однорідної змішаної задачі (типу 1) знаходимо методом відокремлення змінних аналоґічно до прикладу 1. Будемо мати
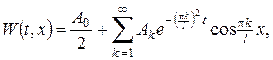
де
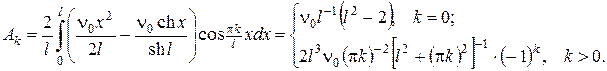
А тоді
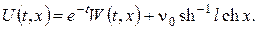
ПРИКЛАД 5 (двовимірна змішана задача). Знайти розподіл температури в однорідній прямокутній пластинці 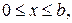
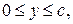 якщо початкова її температура рівна нулеві, край
якщо початкова її температура рівна нулеві, край 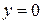 теплоізольований, а на краях
теплоізольований, а на краях 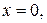
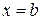 та
та 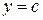 задані закони зміни температури – відповідно 0,
задані закони зміни температури – відповідно 0, 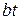 і
і 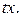 Інтенсивність джерел тепла, розміщених усередині пластинки, рівна
Інтенсивність джерел тепла, розміщених усередині пластинки, рівна 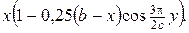
Розв’язання. Схема інтеґрування двовимірної змішаної задачі для рівняння теплопровідності аналоґічна схемі розв’язування змішаної задачі для рівняння коливань прямокутної мембрани (див. [4], розділ ІІ, тема 3, с.146-156).
Відповідна математична модель:
- 15 -
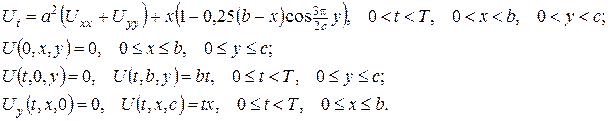
Перший етап. Крайові умови неоднорідні, тому зводимо їх до однорідних підстановкою 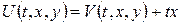 (допоміжна функція, котра повинна справджувати чотири крайові умови, визначається підбором). Тоді для
(допоміжна функція, котра повинна справджувати чотири крайові умови, визначається підбором). Тоді для 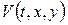 одержимо змішану задачу:
одержимо змішану задачу:
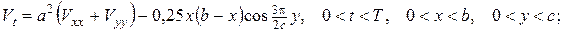 (16)
(16)
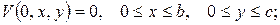 (17)
(17)
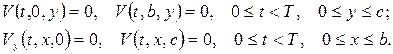
Поскільки вільний член у рівнянні справджує крайові умови, то для знаходження розв’язку застосовний метод Фур’є.
Другий етап. В одержаній змішаній задачі крайові умови однорідні, але рівняння неоднорідне (задача типу 2). Отже, спершу (див. приклад 2) потрібно знайти власні функції задачі Штурма-Ліувілля для відповідної однорідної задачі:
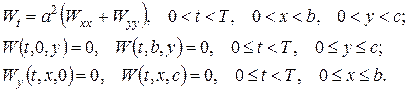
Поклавши 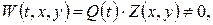 а потім в одержаній двовимірній задачі на власні значення
а потім в одержаній двовимірній задачі на власні значення 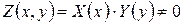 і розв’язавши дві одновимірні задачі Штурма-Ліувілля, знаходимо
і розв’язавши дві одновимірні задачі Штурма-Ліувілля, знаходимо
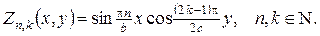
Третій етап. Функцію 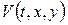 шукаємо у вигляді ряду по знайденій системі власних функцій:
шукаємо у вигляді ряду по знайденій системі власних функцій:
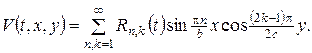 (18)
(18)
Коефіцієнти 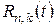 знаходимо підстановкою ряду (18) у рівняння (16) та початкову умову (17). Поставивши відповідні задачі Коші та проінтеґрувавши їх, одержимо:
знаходимо підстановкою ряду (18) у рівняння (16) та початкову умову (17). Поставивши відповідні задачі Коші та проінтеґрувавши їх, одержимо:
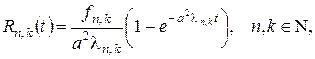 (19)
(19)
де
- 16 -
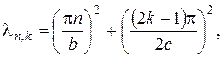
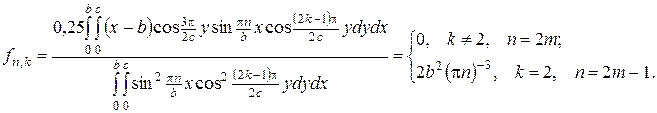 Підставивши (19) у ряд (18), дістанемо функцію
Підставивши (19) у ряд (18), дістанемо функцію 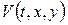 . А тоді
. А тоді