Анализ эффективности функционирования КА

При анализе эффективности КА необходимо учитывать, что появление отказов отдельных систем или значительные изменения их рабочих параметров могут приводить не к полному выходу КА из строя, а лишь к некоторому ухудшению его функционирования в целом.

В общем случае эффективность можно рассматривать как математическое ожидание функции качества, определенной на траекториях процесса

(1.71)

где - функция качества, характеризующая степень выполнения задачи в точках фазового пространства состояний .

Соотношение (1.71 определяет показатель эффективности в общем виде. Конкретный вид показателей эффективности функционирования определяется назначением КА и факторами последствий отказов его систем. В зависимости от выбора фазовых пространств, определяемых спецификой задачи, показатели эффективности могут быть размерными величинами, например, производительность, общий доход, либо безразмерными, например, вероятность выполнения задачи.

Для проведения конкретных расчетов показателя эффективности представим соотношение (1.71 в раскрытом виде. Согласно определению математического ожидания дискретной случайной величины имеем

(1.71)

где - вероятность нахождения КА в i-ом состоянии;

- функция качества, характеризующая степень выполнения задачи при нахождении КА в i-ом состоянии;

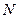- число всевозможных состояний.

Функция качества назначается на основе исследования характера и последствий отказов отдельных систем.

Таким образом, для решения задачи требуется определить вероятности нахождения КА в различных точках фазового пространства состояний.

Анализ математической модели функционирования невосстанавливаемой системы показывает, что переход из одного состояния системы в другое происходит в результате отказа одного из элементов, бывшего исправным в предыдущем состоянии.

При этом предполагается, что за время вероятность более одного перехода, то есть одновременного отказа двух и более элементов есть величина более высокого порядка малости.

Указанные обстоятельства позволяют все состояния системы из 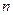элементов, подразделить на упорядоченных групп.

В одну группу включались все состояния, имеющие одинаковое число отказавших элементов. Группы нумеруются так, чтобы номер группы был равен числу отказавших элементов. Тогда численность i-ой группы будет равна . Система с рассмотренной выше структурой будет обладать следующими свойствами:

переходы между состояниями внутри группы исключены,

переходы из состояний группы в состояния группы исключены,

из каждого состояния i-ой группы можно перейти только в состояний -ой группы.

При проведении анализа будем учитывать, что последствия отказов зависят только от типа отказавшего элемента. В дальнейшем функцию качества, соответствующую отказу i-ого элемента обозначаем Ф_i. Соответственно при отказе дух элементов, i-ого и j-ого, функция качества будут равны Ф_ij. Очевидно для безотказного состояния Ф₀ = 1.

При отказе трех и более элементов функции качества будем считать равной 0. В дальнейшем оценим вероятность нахождения системы в различных состояниях.

Очевидно, вероятность нахождения системы в безотказном состоянии P₀ будет равна ее надежности

(1.72)

где - надежность одного элемента.

Для высоконадежных систем приближенно получим

(1.73)

где - вероятность отказа одного элемента.

Соответственно, вероятность нахождения системы в состоянии с одним отказом приближенно можно оценить по соотношению

(1.74)

Аналогично вероятность нахождения системы в состоянии с двумя отказами будет равна

(1.75)

С учетом полученных соотношений, выражение для показателя эффективности (1.71) можно представить в виде

(1.76)

После преобразований получим