Скалярний, векторний та мішаний добуток векторів, їх застосування
Скалярним добутком двох векторів  і
і 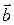 називається число
називається число
S =| 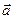 | |
| | 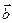 |сos(
|сos( 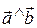 ).
).
Ця операція позначається 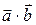 . Зокрема, скалярний квадрат вектора дорівнює квадратові його довжини, тобто
. Зокрема, скалярний квадрат вектора дорівнює квадратові його довжини, тобто 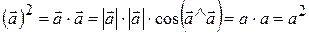 . Якщо один з векторів, що перемножуються, одиничний, то:
. Якщо один з векторів, що перемножуються, одиничний, то:
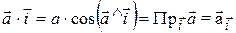 .
.
Властивості скалярного добутку:
1)  ×
×  = ï
= ï  ï2;
ï2;
2)  ×
×  = 0, якщо
= 0, якщо  ^
^  або
або  = 0, або
= 0, або  = 0.
= 0.
3)  ×
×  =
=  ×
×  ;
;
4)  ×(
×(  +
+ 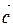 ) =
) =  ×
×  +
+  ×
× 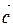 ;
;
5) (m  )×
)×  =
=  ×(m
×(m  ) = m(
) = m(  ×
×  ).
).
Нехай задані вектори у прямокутній системі координат

тоді 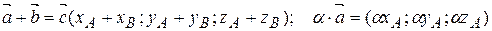 .
.
Якщо розглядати вектори 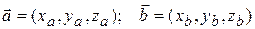 у декартовій прямокутній системі координат, то
у декартовій прямокутній системі координат, то  ×
×  = xa xb + ya yb + za zb.
= xa xb + ya yb + za zb.
Використовуючи отримані рівності, отримуємо формулу для обчислення кута між векторами:
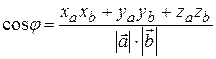 .
.
Якщо скалярний добуток двох векторів дорівнює нулеві, то ці вектори ортогональні. Дійсно, якщо жоден з векторів не нульовий, то, за означенням скалярного добутку, останній може дорівнювати нулеві тільки тоді, коли 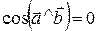 , тобто
, тобто 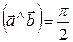 .
.
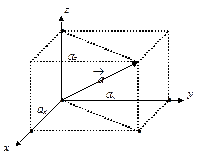
Рис.3.
Якщо скалярний добуток двох векторів дорівнює нулеві, то ці вектори ортогональні. Дійсно, якщо жоден з векторів не нульовий, то, за означенням скалярного добутку, останній може бути рівним нулеві тільки тоді, коли 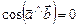 , тобто
, тобто 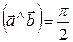 .
.
Якщо вектор представлений через проекції на базисні вектори, то говорять про розкладання вектора 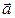 по ортогональному базису. З рисунка видно, що в цьому випадку вектор
по ортогональному базису. З рисунка видно, що в цьому випадку вектор 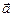 є головною діагоналлю прямокутного паралелепіпеда, ребра якого паралельні осям координат і дорівнюють довжинам проекцій вектора
є головною діагоналлю прямокутного паралелепіпеда, ребра якого паралельні осям координат і дорівнюють довжинам проекцій вектора 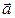 на ці осі. З цього ж рисунка випливає, що модуль вектора
на ці осі. З цього ж рисунка випливає, що модуль вектора 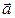 чисельно буде дорівнює
чисельно буде дорівнює
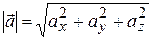 .
.
З означення скалярного добутку випливає, що будь-який вектор, незалежно від типу, можна представити у вигляді:
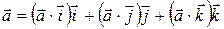 ,
,
де 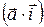 ,
, 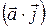 і
і 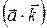 є скалярний добуток вектора
є скалярний добуток вектора 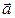 з ортами осей координат.
з ортами осей координат.
У цьому випадку результат являє собою проекцію вектора 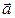 на напрямок одиничного вектора
на напрямок одиничного вектора 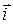 . Отже, будь-який вектор можна представити як
. Отже, будь-який вектор можна представити як 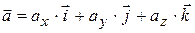 , де
, де 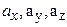 - проекції вектора
- проекції вектора  відповідно на осі 0х, 0у і 0z.
відповідно на осі 0х, 0у і 0z.
З останньої рівності маємо
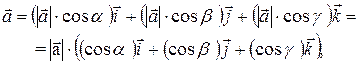
де a, b і g - кути, що утворює вектор 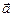 відповідно з осями 0х, 0у і 0z.
відповідно з осями 0х, 0у і 0z.
Лінійно незалежні вектори  ,
, 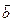 і
і 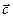 утворюють праву трійку векторів, якщо вони мають таку ж орієнтацію, як відповідно великий, вказівний і середній палець правої руки, у протилежному випадку говорять про ліву трійку векторів.
утворюють праву трійку векторів, якщо вони мають таку ж орієнтацію, як відповідно великий, вказівний і середній палець правої руки, у протилежному випадку говорять про ліву трійку векторів.
Три одиничних вектори i, j, k, попарно ортогональні один одному й утворюючій правій трійці векторів, називають прямокутною декартовою системою координат.
Кутом між векторами 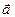 і
і 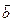 називають такий кут a, не переважаючий p, на який потрібно повернути вектор
називають такий кут a, не переважаючий p, на який потрібно повернути вектор 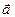 , щоб сполучити його з напрямком вектора
, щоб сполучити його з напрямком вектора  , початок якого повинен збігатися з початком
, початок якого повинен збігатися з початком 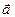 . Кут між векторами позначається (
. Кут між векторами позначається ( 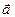 ,
,  ) або (
) або ( 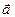 Ù
Ù 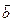 ).
).

Рис.4.
Означення. Векторним добуткомвекторів  і
і  називається вектор
називається вектор 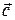 , який задовольняє наступні умови:
, який задовольняє наступні умови:
1) 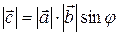 , де j - кут між векторами
, де j - кут між векторами  і
і  ,
,
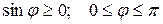
2) вектор 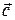 ортогональний векторам
ортогональний векторам  і
і  ,
,
3)  ,
,  і
і 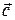 утворюють праву трійку векторів.
утворюють праву трійку векторів.
Векторний добуток позначають: 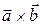 або
або 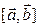 .
.
Властивості векторного добутку векторів:
1) 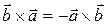 ;
;
2) 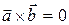 , якщо
, якщо  ïï
ïï  або
або  = 0 або
= 0 або  = 0;
= 0;
3) (m  )´
)´  =
=  ´(m
´(m  ) = m(
) = m(  ´
´  );
);
4)  ´(
´(  +
+ 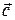 ) =
) =  ´
´  +
+  ´
´ 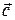 ;
;
5) Якщо задані вектори 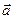 (xa, ya, za) і
(xa, ya, za) і 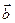 (xb, yb, zb) в декартовій прямокутній системі координат з одиничними векторами
(xb, yb, zb) в декартовій прямокутній системі координат з одиничними векторами 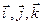 , то
, то
 ´
´  =
= 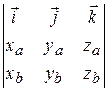 .
.
6) Геометричний зміст векторного добутку – площа паралелограма, побудованого на векторах  і
і  .
.
Означення. Мішаним добуткомвекторів 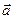 ,
, 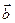 і
і 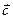 називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора  на вектор, рівний векторному добутку векторів
на вектор, рівний векторному добутку векторів  і
і 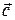 .
.
Позначається 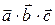 або (
або (  ,
,  ,
, 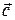 ).
).
Мішаний добуток векторів 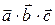 за модулем дорівнює об’єму паралелепіпеда, побудованого на векторах
за модулем дорівнює об’єму паралелепіпеда, побудованого на векторах  ,
,  і
і 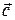 .
.
Властивості мішаного добутку:
1) Мішаний добуток дорівнює нулеві, якщо:
а) хоча б один з векторів дорівнює нулеві;
б) два з векторів колінеарні;
в) вектори компланарні.
2) 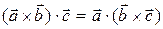 .
.
3) 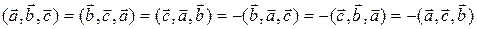 .
.
4) 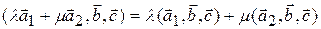 .
.
5) Об’єм трикутної піраміди, утвореної векторами  ,
,  і
і 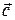 , дорівнює
, дорівнює
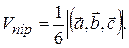
6) Якщо 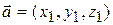 ,
, 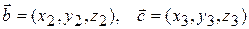 , то
, то
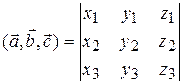 .
.
