ЛЕКЦИЯ № 21. ТЕОРЕМЫ ЛАГРАНЖА И КОШИ

Вопрос 21.1. Теорема Лагранжа.

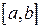Теорема 21.1.(Теорема Лагранжа). Если непрерывна на отрезке и дифференцируема внутри отрезка, то найдется хотя бы одна точка c такая, что 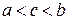и

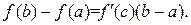
Эта формула носит название формулы конечных приращений Лагранжа (см. рис. 1).

Доказательство. Пусть 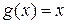, тогда функции и 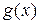удовлетворяют условиям теоремы Коши. Применяя формулу Коши, получим

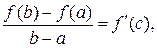
откуда следует формула Лагранжа

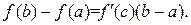
Конец доказательства.

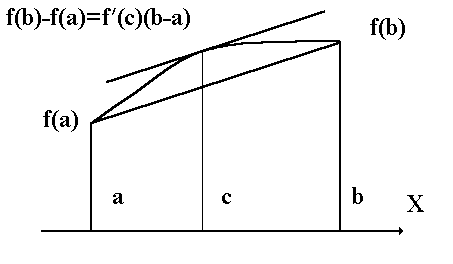
Рис. 1. К доказательству теоремы Лагранжа.

Следствия из теоремы Лагранжа.

Следствие 21.1. Если 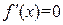для всех x из интервала 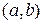, то 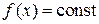на интервале .

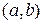Доказтельство. Возьмем две произвольные точки 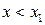из интервала 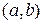и применим формулу Лагранжа 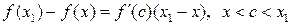. Так как 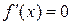, то 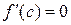и, следовательно, 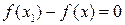. Таким образом, .

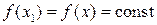Конец доказательство.

Следствие 21.2. Пусть 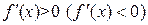на интервале 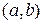, тогда монотонно возрастает (убывает) на интервале .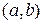

Доказательство. Пусть 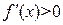на интервале 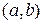, тогда для любых точек 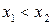из этого интервала 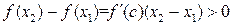, то есть 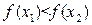, если 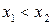. Аналогично рассматривается случай .

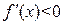Конец доказательства.

Следствие 21.3. Пусть 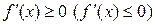на интервале 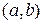, тогда монотонно не убывает (не возрастает) на этом интервале.

Доказательство аналогично доказательству следствия 21.2.

Следствие 21.4. Если 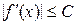на интервале 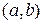, то для непрерывной на отрезке 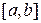и дифференцируемой на 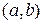функции справедливо неравенство .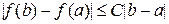

Доказательство.По формуле Лагранжа 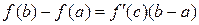. Тогда 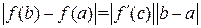. Отсюда .

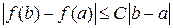Конец доказательства.

Вопрос 21.2. Правила Лопиталя - Бернулли.

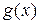Теорема 21.2. Пусть и дифференцируемы на интервале 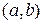и являются бесконечно малыми функциями в окрестности точки a. Если существует (конечный или бесконечный) предел 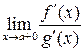, то существует и предел 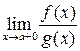, причем оба предела равны.

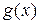Доказатедьство. Так как и бесконечно малые функции, то 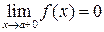и 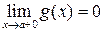. Переопределим функции в точке x=a, положив 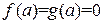. Возьмем любую сходящуюся к a последовательность аргументов из отрезка [a,b] 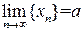. Применяя к отрезку 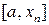теорему Коши, получим

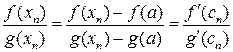
Так как 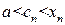, то последовательность 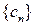сходится к a. Поэтому получим

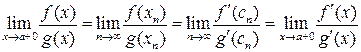
Отсюда следует доказываемая теорема.

Конец доказательства.

Замечание. Теорема с соответствующими изменениями справедлива при .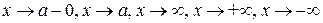

Пример 21.1. .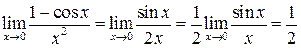

Конец примера.

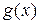Теорема 21.3. Пусть и дифференцируемы на интервале 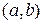и являются бесконечно большими функциями в окрестности точки a. Если существует (конечный или бесконечный) предел 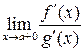, то существует и предел 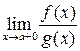, причем оба предела равны.

Замечание. Теорема с соответствующими изменениями справедлива при .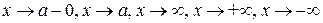

Пример 21.2.

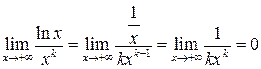
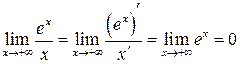
Конец примера.

Замечание. Если для 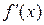и 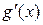выполняются условия одной из теорем, то правила Лопиталя-Бернулли можно применять дважды и более число раз

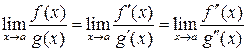
Пример 21.3.

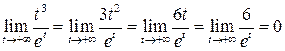
Конец примера.