Построение линий влияния опорных реакций и внутренних усилий в трехшарнирной арке
Определение опорных реакций трехшарнирных арок
При действии внешней нагрузки на трехшарнирную арку (рис. 3,а) в каждой ее опоре возникает по две реакции — горизонтальная и вертикальная; всего, таким образом, имеется четыре опорные реакции. Вертикальные реакции обозначим VА и VB.
Кроме трех уравнений равновесия, которые дает статика для системы сил, расположенных в одной плоскости, для расчета трехшарнирной арки можно составить четвертое уравнение статики, основанное на том, что изгибающий момент в поперечном сечении арки, проведенном через средний шарнир С, равен нулю; следовательно, равна нулю алгебраическая сумма моментов сил, действующих на левую или правую часть арки относительно точки С:
SМс лев =0; SМспр =0.
Из полученных четырех уравнений статики могут быть определены все опорные реакции.
Рекомендуется уравнения статики составлять такие и в такой последовательности, чтобы избежать совместного решения системы уравнений с несколькими неизвестными. Так, сначала можно составить уравнение SМВ = 0 — суммы моментов всех сил относительно шарнира В (см. рис. 3), в которое войдет лишь одна опорная реакция VA. После определения значения VA можно составить уравнение SМС = 0 — суммы моментов сил, действующих на левую часть арки, относительно шарнира С, в которое войдет уже известная реакция VA и неизвестная реакция НА, из этого уравнения находим значение НА. Затем из уравнения SМА =0 — суммы моментов всех сил относительно шарнира А можно найти реакцию VB, а из уравнения SМС = 0 – суммы моментов сил, действующих на правую часть арки, относительно шарнира С, в которое войдет известная реакция VВ и неизвестная реакция НВ, из этого уравнения находим значение НВ.
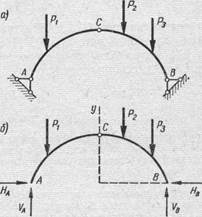
Рис. 3
Для проверки правильности полученных значений реакций рекомендуется затем убедиться в том, что они удовлетворяют условиям SY =0, SХ =0.
Определение изгибающих моментов, поперечных и продольных сил в сечениях трехшарнирной арки
Рассмотрим трехшарнирную арку, нагруженную вертикальной нагрузкой. Наряду с аркой будем рассматривать балку с таким же пролетом и такой же нагрузкой.
Изгибающий момент в сечении «к» трехшарнирной арки равен сумме моментов сил, расположенных слева или справа от сечения, относительно центра тяжести сечения:
Мк = Мк0 – Н×ук. (1)
Поперечная сила в сечениях трехшарнирной арки равна сумме проекций сил, расположенных по одну сторону от сечения, на плоскость сечения:
Qк = Qк0 cos𝜑 – H sin𝜑. (2)
Продольная сила в сечениях трехшарнирной арки равна сумме проекций сил, расположенных по одну сторону от сечения, на касательную к оси арки:
Nк = Qк0 sin𝜑 + Н cos𝜑. (3)
Здесь Мк0 , Qк0 – балочный изгибающий момент и поперечная сила в сечении «к» простой балки с тем же пролетом и нагрузкой; ук – ордината сечения «к»; 𝜑 – угол между касательной и осью абцисс.
Построение линий влияния опорных реакций и внутренних усилий в трехшарнирной арке
Расположим на трехшарнирной арке вертикальную силу Р=1 на расстоянии х от левой опоры и составим уравнения моментов всех сил относительно опорных шарниров:
SМВ = VA l – 1× (l – х)= 0; SМА = – VВ l + 1× х = 0;
Из этих уравнений найдем:
VA = (l – х)/ l; VВ = х/ l.
Выражения VA и VВ совпадают с выражениями опорных реакций, полученными для простой балки. Следовательно, линии влияния VA и VВ ничем не отличаются от линий влияния опорных реакций простой балки на двух опорах.
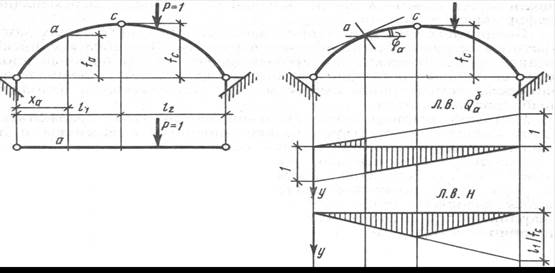
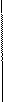


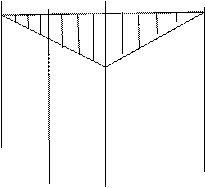
 Л.в. Н
Л.в. Н
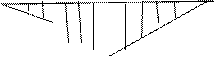
Л.в. Nк
 | |||
 | |||

 l/4f
l/4f



 Л.в. Мк Л.в. Qк
Л.в. Мк Л.в. Qк
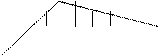 |  | ||











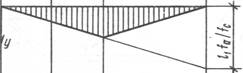
Рис. 4. Построение л.в. Мк, Qк, Nк
Распор Н определяется уравнением Н = МС0/f, из которого следует, что линия влияния Н имеет такой же вид, как и линия влияния балочного момента МС0, и отличается от нее лишь постоянным множителем 1/ f; в частном случае, когда l1 = l2 = l/2, ее ордината под шарниром С равна l/(4f).
В линейно деформируемых системах с линиями влияния можно производить простые арифметические действия сложения, вычитания и умножения на постоянную величину, как с обычными числами или векторами. Учитывая это, можно воспользоваться для построения линий влияния моментов, поперечных и продольных сил формулами 1, 2, 3.
В сечении «к» л. в. Qк имеет скачок, равный cos𝜑к, а л. в. Nк – скачок, равный sin𝜑к.
Линии влияния усилий трехшарнирной арки показывают существенное отличие ее работы от балки. Так, ординаты л. в. Мк значительно меньше ординат Мк0, л. в. Мк двузначна и имеет между опорами нулевую точку; л. в. Qк имеет также значительно меньшие ординаты, чем л. в. Qк0. Кроме того, в отличие от балки появилась л. в. Nк, причем ее ординаты значительны и в промежутке между опорами при обычном очертании арки имеют постоянный знак сжатия.
