Несобственные интегралы от непрерывной функции по бесконечному промежутку (первого рода)

Пусть отрезок 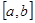числовой оси неограничен. Это возможно в трех случаях: 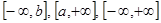. Определим несобственные интегралы как пределы

,

,

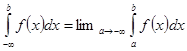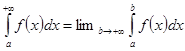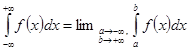. В последнем интеграле a и b независимо друг от друга стремятся к 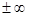. Если 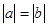, то предел в правой части последнего равенства называется главным значением несобственного интеграла.

Если эти пределы существуют и конечны, то несобственные интегралы называются сходящимися. Если предел не существует или бесконечен, то такой несобственный интеграл называется расходящимся.

Если сходятся интегралы от функций 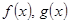, то сходятся интегралы от функций 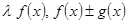. Это следует из теорем о пределах.

Пример. 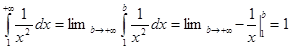, интеграл сходится.

Пример. 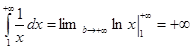, интеграл расходится.

Пример. 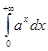сходится при 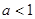и расходится при 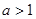. Проверьте это.

Рассмотрим интеграл Дирихле .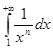

.

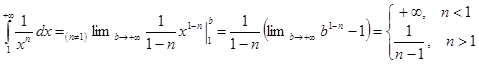При 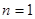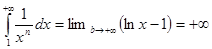, интеграл расходится.

Итак, несобственный интеграл Дирихле первого рода 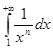сходится при 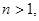расходится при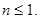

Признаки сравнения несобственных интегралов(достаточные признаки сходимости и расходимости несобственных интегралов).

1 признак. Теорема.Пусть при 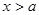выполнено неравенство .

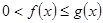Если интеграл 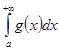сходится, то и интеграл 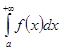сходится.

Если интеграл 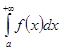расходится, то и интеграл 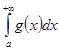расходится.

Доказательство. Проинтегрируем неравенство 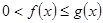на отрезке ,

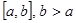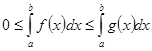. Так как обе функции на отрезке имеют только положительные значения, то интегралы от этих функций представляют собой возрастающие функции от верхнего предела b.

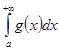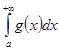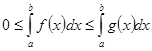
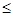
Если сходится ( = I), то при любом b > a 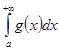= I (I – конечное число).

Поэтому 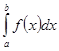- монотонно возрастающая, ограниченная функция верхнего предела интегрирования b. Следовательно, по теореме Вейерштрасса этот интеграл как функция b имеет предел

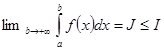, т.е. интеграл 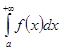сходится.

Пусть теперь 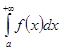расходится. Если 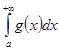сходится, то по доказанному и 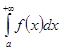сходится, противоречие. Теорема доказана.

Вообще-то, все было ясно из геометрического смысла определенного интеграла как площади криволинейной трапеции под графиком функции. Если значения одной функции больше, чем значения другой функции, то и соответствующая криволинейная трапеция имеет большую площадь. И если эта площадь конечна, то и меньшая площадь конечна. А если меньшая площадь бесконечна, то и большая площадь бесконечна. Но строгое доказательство не подведет, а «очевидное» иногда подводит.

2 признак сравнения. Теорема.Пусть при x>a 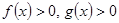. Если существует конечный предел 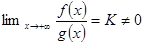, то интегралы 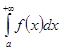, , 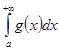сходятся или расходятся одновременно (если один сходится, то и другой сходится, если один расходится, то и другой расходится).

Доказательство. Из определения предела следует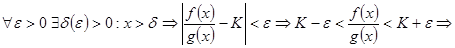

.

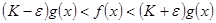Если интеграл 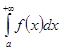сходится, то по первому признаку сравнения сходится интеграл 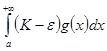, а, следовательно, сходится интеграл 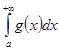. Если интеграл 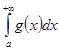сходится, то сходится интеграл 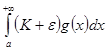, а, следовательно, по первому признаку сравнения сходится интеграл 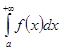. Пусть интеграл 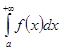расходится. Если интеграл 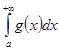сходится, то по первому признаку сравнения сходится интеграл 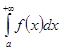, противоречие. Пусть интеграл 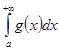расходится. Если интеграл 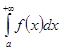сходится, то по первому признаку сравнения сходится интеграл 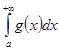, противоречие. Теорема доказана.

Эталонами служат обычно интегралы Дирихле или интегралы от показательной функции.

Пример. 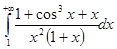сходится по второму признаку сравнения, интеграл сравнения .

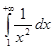Пример. 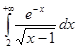сходится по первому признаку, интеграл сравнения

.
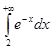