РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 9

Тема: «Устойчивость центрально сжатых стержней»

Цель работы:

Расчет на устойчивость с использованием коэффициента продольного изгиба, подбор сечений.

Студент должен знать:

1. формулу критического напряжения;

1. условия устойчивости по предельному состоянию.

Студент должен уметь:

1. выполнять расчеты сжатых стержней по формуле Эйлера с использованием коэффициента продольного изгиба.

Вопросы для самоконтроля:

1. В чем заключается сущность явления продольного изгиба?
2. Какая сила называется критической?
3. Что называется запасом устойчивости?
4. Как в общем виде записывается формула Эйлера?
5. Что называется приведенной длиной сжатого стержня?
6. Каковы коэффициенты приведения для случаев: шарнирно-закрепленных концов; один конец свободен, другой – защемлен; оба конца защемлены?
7. Что называется гибкостью стержня?
8. Укажите пределы применимости формулы Эйлера.
9. Что такое коэффициент продольного изгиба ?
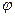10. Как рассчитываются центрально сжатые стержни с применением коэффициента продольного изгиба?
11. В чем суть подбора поперечного сечения центрально сжатых элементов?

Методические указания

Прямолинейные стержни под действием сжимающих усилий встречаются очень часто. Это центрально сжатые стержни ферм, стойки, колонны, которые под действием нагрузки укорачиваются, сохраняя свою прямолинейную форму. В некоторых случаях стержень может искривиться (выпучиться). Это явление называется потерей устойчивости или продольным изгибом. Потеря устойчивости наступает тем скорее, чем больше гибкость стержня 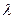, которая зависит от ряда факторов: длины стержня 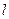, условия закрепления концов стержня, а также радиуса инерции поперечного сечения стержня

i_мин = .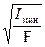

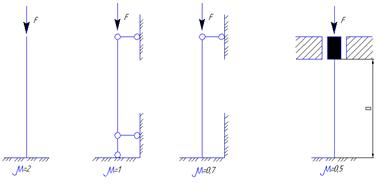
рис. 23

В зависимости от условия закрепления концов стержня определяют коэффициент приведения длины 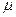, величину которого для четырех случаев необходимо знать на память (рис. 21). Гибкость стержня определяется по формуле

.

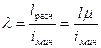В зависимости от материала, из которого выполнен центрально-сжатый стержень, а также гибкости 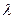определяется коэффициент снижения напряжения (коэффициент продольного изгиба) 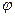. При расчете на устойчивость по допускаемым напряжениям должно соблюдаться условие:

.

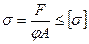При расчете на устойчивость по расчетным предельным состояниям должно соблюдаться следующее условие:

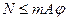или .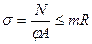

Для стали Ст3 коэффициент продольного изгиба 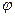определяется по приложению 2.

Пример.Подобрать сечение центрально-сжатой стойки, выполненной из двух двутавров, сваренных по полкам по всей длине (рис. 24). Длина стойки l = 8 м; закрепление обоих концов жесткое; материал сталь Ст3, для нее 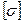= 160 МН/м² =

== 160 МПа; сжимающая сила F = 1,7 МН.

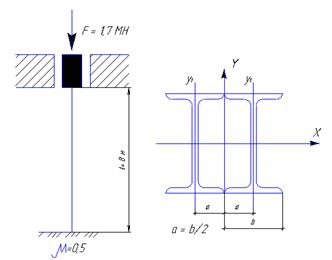
рис. 24

Решение

1. Подбор сечения сжатой стойки начнем с расчета на устойчивость, определив требуемую площадь поперечного сечения по формуле

,

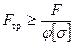где кроме искомого значения А_тр неизвестен коэффициент продольного изгиба 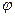. Поэтому расчет приходится вести путем последовательных приближений, задаваясь значением коэффициента 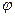. Для первого приближения возьмем 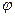= 0,7, тогда требуемая площадь сечения

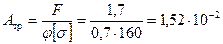м².

2. Требуемая площадь сечения одного двутавра

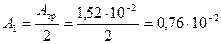м².

3. В таблице сортамента ГОСТ 8239-72 найти двутавр № 40, для которого

А_табл = 72,6 см² = 72,6 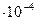м²; b = 155 мм = 155 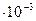м; i_х 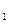= 16,2 см = 16,2 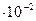м;

i_у 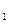= 3,03 см = 3,03 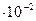м; I_х = 19062 см⁴ = 19062 м⁴.

4. Найти гибкость стойки

,

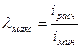где l_расч – расчетная длина стержня, l_расч = ;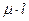

i_мин - наименьший радиус инерции поперечного сечения стойки.

Относительно оси х – х радиус инерции сечения из двух двутавров № 40 берем из сортамента i_х 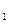= 16,2 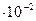м, определить радиусы инерции сечения

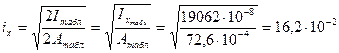м.

Радиус инерции относительно оси у-у

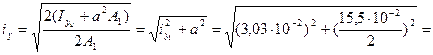
= 8,32 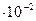м,

следовательно, i_мин = i_у = 8,32 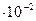м.

Тогда

.

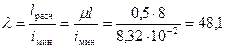5. Из приложения 2 этому значению гибкости соответствует 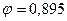, что значительно больше того значения 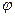, которым мы задавались ранее ( 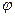= 0,7), поэтому возьмем их среднее значение

.

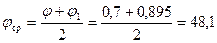6. Определить требуемую площадь сечения

А_треб = 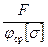= 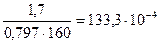м².

На один двутавр приходится:

А₁ = 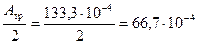м² = 66,7 см².

7. Из сортамента двутавров требуемой площади удовлетворяет двутавр № 36, у которого А_табл = 61,9 см² = 61,9 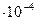м²; b = 145 мм = 145 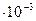м; 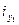= 2,89 см = 2,89 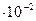м; 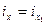= 14,7 см = 14,7 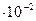м.

8. Найти i_мин сечения, составленного из двух двутавров № 36,

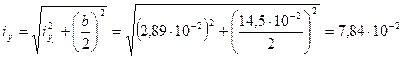м.

Тогда i_мин = i_у = 7,84 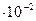м и .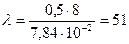

9. Выбрать коэффициент продольного изгиба:

Из приложения 2 находим .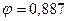

10. Проверить напряжение в сечении сжатой стойки

.

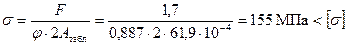Недонапряжение составляет 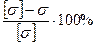: 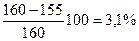, что в пределах допускаемого.

Задание для расчетно-графической работы № 9.Подобрать сечение центрально-жатой стойки, выполненной из двух двутавров (или двух равнополочных уголков или двух швеллеров), сваренных по полкам по всей длине. Исходные данные взять из табл. 4 и рис.25. Материал – сталь Ст 3, для нее 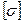= 160 МПа.

Таблица 4

Вариант	Схема	, м	F, МН	Вариант	Схема	, м	F, МН
	I		1,8		VI		1,9
		1,9			1,6
		2,0			1,5
	II		1,9		VII		2,0
		1,8			1,5
		2,0			1,6
	III		1,7		VIII		1,8
		1,6			2,3
		1,9			1,7
	IV		2,2		IX		1,6
		1,8			1,7
		1,7			1,9
		1,7			2,3
	V		1,8		X		2,1
		1,9			2,0
		1,6			1,9
		2,1			1,8

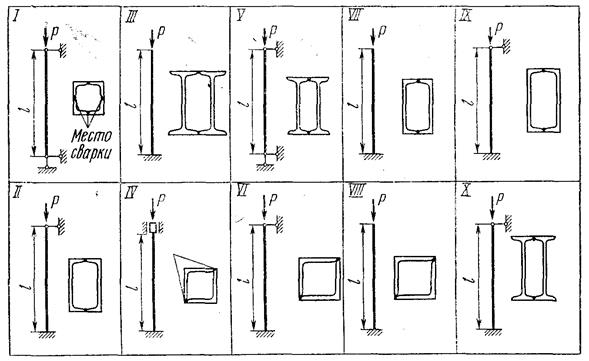
рис. 25