Сызықтық теңдеулер жүйесін шешу тәсілдері.
Дәріс.
Дәріс тақырыбы:Матрицалар және анықтауыштар.
Дәріс жоспары:
§ Матрицалар.
§ Матрицаларға амалдар қолдану.
§ Матрицаларға қолданылатын амалдар қасиеттері.
§ Анықтауыштар.
§ Анықтауыштыңқасиеттері.
§ Әдебиеттер.
§ Бақылау сұрақтары.
Матрица деп, m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кестені айтады.
Матрица латынның үлкен әріптерімен белгіленеді A,B,C,… және былай жазылады:
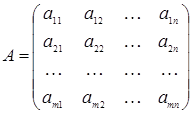
немесе қысқаша 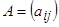 , мұндағы
, мұндағы 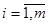 (яғни
(яғни 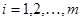 ) – жолдың нөмірі,
) – жолдың нөмірі, 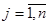 (яғни
(яғни 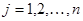 ) – бағанның нөмірі.
) – бағанның нөмірі.
А матрицасын 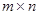 өлшемді матрица дейді және оны
өлшемді матрица дейді және оны 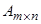 деп жазады. Матрицаны құрайтын
деп жазады. Матрицаны құрайтын 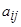 сандарын сол матрицаның элементтері дейді.
сандарын сол матрицаның элементтері дейді. 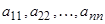 элементтері бас диагоналді құрайды.
элементтері бас диагоналді құрайды. 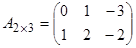 -
-  - өлшемді матрица.
- өлшемді матрица.
Бір жолдан тұратын матрицаны жол-матрица дейді. Бір бағаннан тұратын матрицаны баған-матрица дейді. Егер матрицаның жолдарының саны бағандарының санына тең болса, ондай матрицаны квадрат матрицадейді. Оның өлшемі 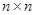 болады.
болады.
Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.
Егер диагональ матрицаның бас диагоналі бір сандарынан тұрса, онда ондай матрицаны бірлік матрица дейді және оны Е деп белгілейді.
Егер квадрат матрицаның бас диагоналінің бір жағына орналасқан элементтері түгелдей нөлге тең болса, онда оны үшбұрышты матрица дейді.
Егер матрицаның барлық элементтері нөлге тең болса, онда ондай матрицаны
нөлдік матрица дейді. Мысалы. а) квадрат; б) диагональ; в) бірлік; г) нөлдік матрицалар:
а) 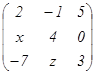 ; б)
; б) 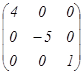 ; в)
; в) 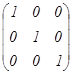 ; г)
; г) 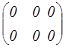 .
.
А матрицасының жолдарын сәйкес бағандар етіп алмастырғаннан пайда болған матрицаны транспонирленген матрица деп атайды және оны 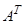 деп белгілейді. Транспонирлеу амалының қасиеттері:
деп белгілейді. Транспонирлеу амалының қасиеттері: 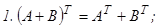
1-мысал. 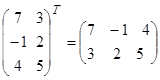
Матрицаларға амалдар қолдану.Қосу амалы амалы өлшемдері бірдей матрицалар үшін ғана енгізіледі. Екі 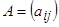 және
және 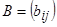 матрицаларының қосындысы деп, элементтері
матрицаларының қосындысы деп, элементтері
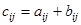 болатын
болатын 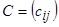 матрицасын айтады және оны
матрицасын айтады және оны 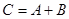 деп белгілейді.
деп белгілейді.
2-мысал. 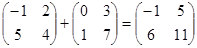
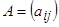 матрицасын
матрицасын 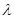 санына көбейту деп әрбір элементі
санына көбейту деп әрбір элементі 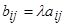 болатын
болатын 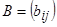 матрицасын айтады.
матрицасын айтады.
3-мысал. 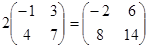 -А=(-1)А матрицасын А матрицасына қарама-қарсы матрица деп атайды. Олай болса, матрицалардың айырымын былай анықтауға болады:
-А=(-1)А матрицасын А матрицасына қарама-қарсы матрица деп атайды. Олай болса, матрицалардың айырымын былай анықтауға болады: 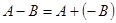
Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері:
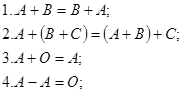
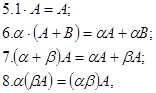
мұндағы  матрицалар,
матрицалар, 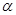 және
және 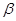 - сандар.
- сандар.
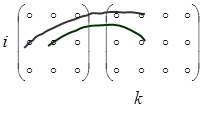
Екі матрицаны көбейту амалы бірінші матрицаның бағандарының саны екінші матрицаның жолдарының санына тең болғанда ғана енгізіледі. 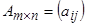 матрицасының
матрицасының 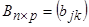 матрицасына көбейтіндісі деп элементтері
матрицасына көбейтіндісі деп элементтері
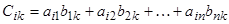 ,
, 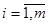 ,
, 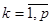
болатын 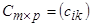 матрицасын айтады. Схемалық түрде былай көрсетуге болады:
матрицасын айтады. Схемалық түрде былай көрсетуге болады:
 |

4-мысал. 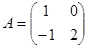 ,
, 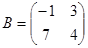
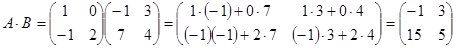
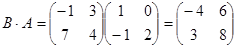 , осыдан
, осыдан 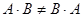
Егер 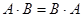 болса, онда А және В матрицалары алмастырылатын матрицалар деп аталады.
болса, онда А және В матрицалары алмастырылатын матрицалар деп аталады.
Матрицаларды көбейту амалының қасиеттері:
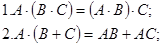
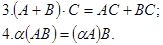
Анықтауыштар.Анықтауыш сатылы түрде анықталады.
1) Кезкелген сан бірінші ретті анықтауыш.
2) Өлшемділігі 2-ге тең квадрат матрица 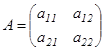 үшін
үшін 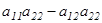 саны (мұндағы
саны (мұндағы 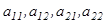 - нақты сандар) А матрицасының анықтауышы немесе 2-ші ретті анықтауыш деп аталады және ол
- нақты сандар) А матрицасының анықтауышы немесе 2-ші ретті анықтауыш деп аталады және ол 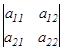 ,
, 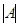 ,
, 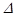 ,
, 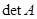 деп белгіленеді. Сонымен
деп белгіленеді. Сонымен
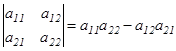
5-мысал. 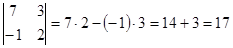
3) 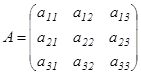 - 3-ші ретті матрица болсын.
- 3-ші ретті матрица болсын.
А матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:
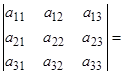
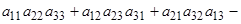
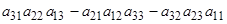 .
.














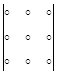 Бұл формуланы жеңіл есте сақтау үшін алғашқы оң таңбалы үш қосылғышты
Бұл формуланы жеңіл есте сақтау үшін алғашқы оң таңбалы үш қосылғышты 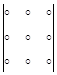 схемасы бойынша, ал қалған үш теріс таңбалы қосылғыштарды схемасы бойынша есептелетіндігін ескеру қажет.
схемасы бойынша, ал қалған үш теріс таңбалы қосылғыштарды схемасы бойынша есептелетіндігін ескеру қажет.

 4)
4) 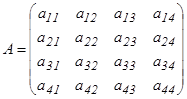 квадрат матрицасының
квадрат матрицасының 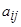 элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны
элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны 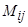 деп белгілейді. Ал
деп белгілейді. Ал 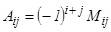 саны
саны 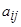 элементінің алгебралық толықтауышы деп аталады. Онда
элементінің алгебралық толықтауышы деп аталады. Онда 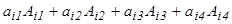 саны 4-ші ретті анықтауыш деп аталады және ол
саны 4-ші ретті анықтауыш деп аталады және ол 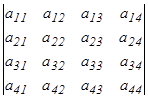 түрінде белгіленеді. Дәл осылай 5-ретті анықтауыш анықталады:
түрінде белгіленеді. Дәл осылай 5-ретті анықтауыш анықталады:
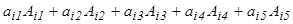 (1.1)
(1.1)
Осылайша кезкелген 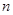 -ші ретті анықтауышты
-ші ретті анықтауышты 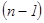 -ші ретті анықтауыштар арқылы анықтаймыз.
-ші ретті анықтауыштар арқылы анықтаймыз.
(1.1) формуласы анықтауышты кез келген жолдың элементтері арқылы жіктеу деп аталады.
6-мысал. 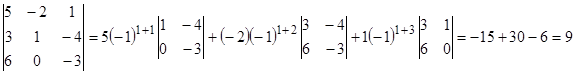
Анықтауыштың қасиеттері:
1. Анықтауыштың жолдарын сәйкес бағандармен алмастырғаннан анықтауыштың мәні өзгермейді.
2. Егер анықтауыштың қандай да бір жолы (бағаны) тек нөлден тұрса, онда анықтауыш нөлге тең.
3.Егер анықтауыштың екі жолы (бағаны) пропорционал болса, онда анықтауыш нөлге тең.
4. Жолдың (бағанның) ортақ көбейткішін анықтауыштың алдына шығарып жазуға болады.
5.Егер анықтауыштың екі жолын (бағанын) алмастырса, онда анықтауыштың таңбасы өзгереді.
6. Егер қандай да бір жолдың (бағанның) элементтеріне кез келген санға көбейтілген басқа жолдың сәйкес элементтерін қосқаннан анықтауыш өзгермейді.
Әдебиеттер: 1 нег.[5-20], 11 қос. [92-115]
Бақылау сұрақтар:
1. Екінші ретті анықтауыш деген не? 4-ретті анықтауыш деген не? Анықтауыштардың
негізгі қасиеттерін атаңыз.
2. Матрицаның анықтауыштан айырмашылығы неде? Матрицаларға қолданылатын амалдарды атаңыз.
3. Екі матрицаны көбейту қай кезде орындалады?
Дәріс.
Дәріс тақырыбы:Сызықтық алгебралық теңдеулер жүйесі.
Дәріс жоспары:
§ Матрицаның рангі.
§ Матрицарангін табу әдістері.
§ Сызықтық алгебралықтеңдеулержүйесі.
§ Сызықтықтеңдеулержүйесін шешу тәсілдері.
§ Әдебиеттер.
§ Бақылау сұрақтары.
А матрицасының рангі деп осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады және оны  ,
,  немесе
немесе  деп белгілейді.
деп белгілейді. 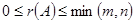 болады, мұндағы
болады, мұндағы 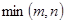 - m және n сандарының кішісі.
- m және n сандарының кішісі.
1-мысал. 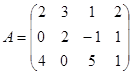 матрицасының рангін табыңыз.
матрицасының рангін табыңыз.
1-әдіс. Минорлар әдісі. Бұл матрицаның рангі 3-тен аспайды. Сондықтан 3-ші ретті минорлар құрамыз. Егер 3-ші ретті минорлардың ішінде бір нөлге тең емес минор табылса, онда ранг 3-ке тең болады. Ал 3-ші ретті минорлардың бәрі нөлге тең болса, онда минор 2-ге не 1-ге тең болады. Оны білу үшін тағы 2-ші ретті минорлар құрамыз. Олардың ішінде бір нөлге тең емес минор табылса, онда ранг 2-ге тең болады. Ал 2-ші ретті минорлардың бәрі нөлге тең болса, минор 1-ге тең.
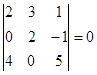 ,
, 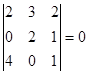 , 3-ші ретті минорлардың бәрі нөлге тең. Олай болса, 2-ші ретті минорлар құрамыз:
, 3-ші ретті минорлардың бәрі нөлге тең. Олай болса, 2-ші ретті минорлар құрамыз: 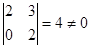 . Демек ранг 2-ге тең, яғни
. Демек ранг 2-ге тең, яғни 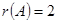
2-әдіс. Элементар түрлендіру әдісі. Матрицаны элементар түрлендіру деп:
1. матрицаның екі жолын (бағанын) ауыстыру;
2. матрицаның жолын (бағанын) нөлге тең емес санға көбейту;
3. бір жол (баған) элементтеріне басқа жолдың (бағанның) сәйкес қандай да бір санға көбейтілген элементтерін қосу амалдарын айтады.
Элементар түрлендіру арқылы алынған матрицаны бастапқы матрицаға эквивалентті матрица дейді және орталарына ~ белгісі қойылады. Матрицаның рангін табу үшін элементар түрлендіруді пайдаланып, матрицаны сатылы түрге келтіреміз.
Теорема. Матрицаны элементар түрлендіргеннен оның рангі өзгермейді.
2-мысал. 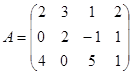 ~
~ 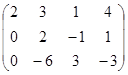 ~
~ 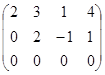 . Демек ранг 2-ге тең, яғни
. Демек ранг 2-ге тең, яғни 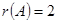 .
.
Кері матрица.Егер 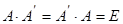 шарты орындалса, онда
шарты орындалса, онда 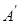 матрицасын
матрицасын 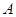 матрицасына кері матрица дейді және оны
матрицасына кері матрица дейді және оны 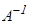 түрінде белгілейді. Мұндағы
түрінде белгілейді. Мұндағы 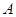 ,
, 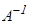 ,
, 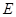 матрицалары бірдей өлшемді квадрат матрицалар.
матрицалары бірдей өлшемді квадрат матрицалар.
Ескерту: Егер 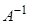 матрицасы бар болса, онда ол жалғыз болады.
матрицасы бар болса, онда ол жалғыз болады.
Теорема. КвадратА матрицасына кері матрица табылуы үшін 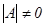 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті. 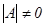 болғанда кері матрица
болғанда кері матрица 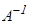 былайша есептелінеді
былайша есептелінеді 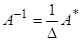 .
.
Мұндағы 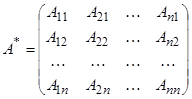 алгебралық толықтауыштардан түзілген матрица.
алгебралық толықтауыштардан түзілген матрица.
3-мысал. 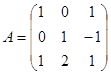 матрицасына кері матрица табыңыз.
матрицасына кері матрица табыңыз. 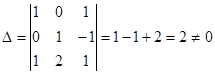 .
.
Олай болса,
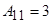 ,
, 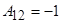 ,
, 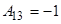 ,
, 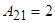 ,
, 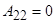 ,
, 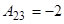 ,
, 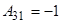 ,
, 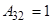 ,
, 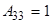
Сонда кері матрица былай болады: 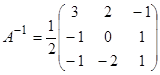 =
=  .
.
Сызықтық алгебралық теңдеулер жүйесі.n белгісізі бар m теңдеулер жүйесі былай жазылады:
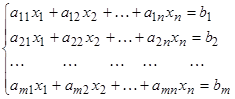
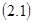
мұндағы 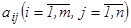 жүйенің коэффициенттері, ал
жүйенің коэффициенттері, ал 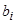 - бос мүшелер деп аталады.
- бос мүшелер деп аталады.  жүйені матрицалық түрде былай жазуға болады
жүйені матрицалық түрде былай жазуға болады 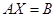 немесе
немесе
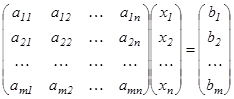 , мұндағы А=
, мұндағы А= 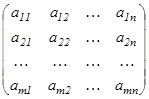 жүйе матрицасы
жүйе матрицасы

A X B
деп аталады.
Егер 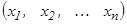 сандар жиыны
сандар жиыны 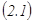 теңдеулер жүйесін тепе-теңдікке айналдырса, онда бұл сандар жиыны осы жүйенің шешімі деп аталады.
теңдеулер жүйесін тепе-теңдікке айналдырса, онда бұл сандар жиыны осы жүйенің шешімі деп аталады.
Егер теңдеулер жүйесінің кемінде бір шешімі бар болса, онда жүйе үйлесімді деп аталады, ал жүйенің бір де шешімі болмаса, онда жүйе үйлесімсіздеп аталады.
Егер А матрицасын бос мүшелерден тұратын бағанмен толықтырса, онда пайда болған матрицаны кеңейтілген матрица дейді және оны 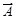 деп белгілейді. Сонымен
деп белгілейді. Сонымен
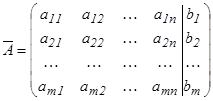
Сызықтық теңдеулер жүйесін шешу тәсілдері.
1. Крамер ережесі.n белгісізі бар n теңдеулер жүйесі берілсін
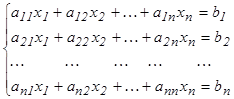
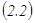
Мұндай жүйенің А матрицасы квадрат матрица болады.
Теорема. Егер 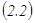 жүйесі үшін
жүйесі үшін 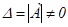 болса, онда жүйенің жалғыз шешімі былайша табылады:
болса, онда жүйенің жалғыз шешімі былайша табылады:
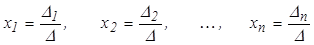
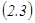
мұнда 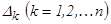 -
- 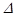 анықтауышындағы
анықтауышындағы 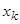 белгісіздерінің коэффициеттерін бос мүшелермен алмастырғаннан пайда болған анықтауыш.
белгісіздерінің коэффициеттерін бос мүшелермен алмастырғаннан пайда болған анықтауыш. 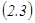 Крамер формуласы деп аталады.
Крамер формуласы деп аталады.
4-мысал. 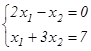 жүйесін Крамер ережесімен шешу керек.
жүйесін Крамер ережесімен шешу керек.
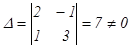 ,
, 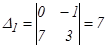 ,
, 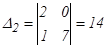
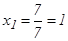 ,
, 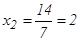 Жауабы:
Жауабы: 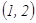
2. Матрицалық әдіс.n белгісізі бар n теңдеулер жүйесі, яғни 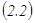 жүйе берілсін. Жүйені матрицалық түрде былай жазамыз
жүйе берілсін. Жүйені матрицалық түрде былай жазамыз 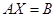
Теорема.Егер 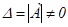 болса, онда
болса, онда 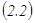 жүйесінің
жүйесінің 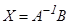 теңдігімен анықталатын жалғыз шешімі бар.
теңдігімен анықталатын жалғыз шешімі бар.
5мысал. 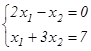 жүйесін матрицалық әдіспен шешу керек.
жүйесін матрицалық әдіспен шешу керек.
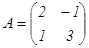 ,
, 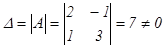 ,
, 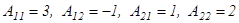
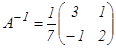 ,
, 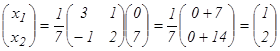 , Жауабы:
, Жауабы: 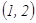
3. Гаусс әдісі.n белгісізі бар m теңдеулер жүйесі, яғни 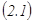 берілсін. Жүйені Гаусс әдісімен шешу екі кезеңнен тұрады. Бірінші кезеңде (тік жүріс) жүйе трапеция тәріздес түрге келтіріледі.
берілсін. Жүйені Гаусс әдісімен шешу екі кезеңнен тұрады. Бірінші кезеңде (тік жүріс) жүйе трапеция тәріздес түрге келтіріледі.
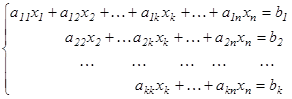 – трапеция тәріздес жүйе.
– трапеция тәріздес жүйе.
Мұнда 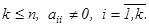
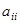 коэффициенттері жүйенің негізгі элементтері деп аталады.
коэффициенттері жүйенің негізгі элементтері деп аталады.
Екінші кезіңде (кері жүріс) мүмкін болса, шыққан жүйеден біртіндеп белгісіздерді табады. Практикада жүйемен емес кеңейтілген матрицамен істеген ыңғайлы болады. Сондықтан жүйені Гаусс әдісімен шешу үшін кеңейтілген матрица құрып,оны элементарлық түрлендірудің көмегімен трапеция тәріздес түрге келтіреді. Бұл жағдайда 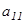 коэффициентінің 1-ге тең болғаны ыңғайлы. Ол үшін теңдеулердің орындарын ауыстыру керек немесе теңдеудің екі жағын да
коэффициентінің 1-ге тең болғаны ыңғайлы. Ол үшін теңдеулердің орындарын ауыстыру керек немесе теңдеудің екі жағын да 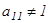 бөлу керек. Содан соң қайтадан жүйе құрып, сол жүйені шешеміз.
бөлу керек. Содан соң қайтадан жүйе құрып, сол жүйені шешеміз.
6-мысал. 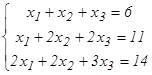 жүйесін Гаусс әдісімен шешу керек.
жүйесін Гаусс әдісімен шешу керек.




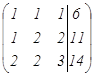
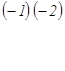 ~
~ 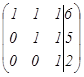 Екінші матрицаның екінші жолын алу үшін бірінші жолды
Екінші матрицаның екінші жолын алу үшін бірінші жолды 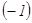 -ге көбейтіп, екінші жолға қостық, ал үшінші жолын алу үшін бірінші жолды
-ге көбейтіп, екінші жолға қостық, ал үшінші жолын алу үшін бірінші жолды 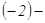 ге көбейтіп, үшінші жолға қостық. Жүйе матрицасы үшбұрышты түрге келді. Енді қайтадан матрицадан жүйеге көшейік және соңғы жолдан бастап жазайық.
ге көбейтіп, үшінші жолға қостық. Жүйе матрицасы үшбұрышты түрге келді. Енді қайтадан матрицадан жүйеге көшейік және соңғы жолдан бастап жазайық.
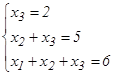 . Осыдан
. Осыдан 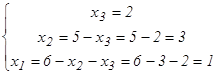 . Жауабы:
. Жауабы: 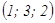
Теорема (Кронекер-Капелли)  жүйе үйлесімді болуы үшін жүйенің матрицасының рангі кеңейтілген матрицаның рангіне тең болуы қажетті және жеткілікіті, яғни
жүйе үйлесімді болуы үшін жүйенің матрицасының рангі кеңейтілген матрицаның рангіне тең болуы қажетті және жеткілікіті, яғни 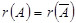 .
.
Әдебиеттер: 1 нег.[ 20-41], 11 қос. [115-135].
Бақылау сұрақтар:
1. Матрицаның рангісінің анықтамасын беріңіз.
2. Кері матрицаның анықтамасын беріңіз.
3. Кері матрица қалай есептелінеді?
4. Сызықтық теңдеулер жүйесін шешудің әдістерін айтыңыз.
Дәріс.
Дәріс тақырыбы:Векторлар. Скалярлық көбейтінді.
Дәріс жоспары:
§ Векторлар.
§ Векторларға қолданылатын сызықтық амалдар.
§ Векторлардың сызықтық тәуелділігі.
§ Базис.
§ Векторларды координат өстерінің орттары арқылы жіктеу.
§ Координаттарымен берілген векторларға амалдар қолдану.
§ Векторлардың скаляр көбейтіндісі.
§ Әдебиеттер.
§ Бақылау сұрақтары.
Вектор деп бағытталған кесіндіні айтады, яғни кесіндінің белгілі бір ұзындығы және бағыты болады. Егер А – вектордың басы, ал В –вектордың ұшы болса, онда вектор 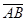 немесе
немесе 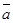 символымен белгіленеді.
символымен белгіленеді. 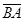 векторы
векторы 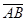 векторына қарама-қарсы вектор деп аталады (оның басы В нүктесінде, ал ұшы А нүктесінде орналасқан).
векторына қарама-қарсы вектор деп аталады (оның басы В нүктесінде, ал ұшы А нүктесінде орналасқан). 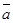 векторына қарама-қарсы векторды
векторына қарама-қарсы векторды 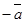 деп белгілейді.
деп белгілейді. 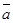 векторының ұзындығынемесе модулідеп
векторының ұзындығынемесе модулідеп 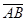 кесіндісінің ұзындығын айтады және оны
кесіндісінің ұзындығын айтады және оны 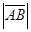 немесе
немесе 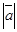 деп белгілейді. Ұзындығы нөлге тең векторды нөлдік вектор деп атайды және ол
деп белгілейді. Ұзындығы нөлге тең векторды нөлдік вектор деп атайды және ол 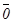 деп белгіленеді. Нөлдік вектордың бағыты болмайды.
деп белгіленеді. Нөлдік вектордың бағыты болмайды.
Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны 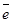 деп белгілейді. Егер бірлік вектордың бағыты
деп белгілейді. Егер бірлік вектордың бағыты 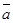 векторының бағытымен сәйкес келсе, онда ол
векторының бағытымен сәйкес келсе, онда ол 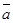 векторының орты деп аталады және
векторының орты деп аталады және 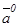 деп белгіленеді.
деп белгіленеді.
Параллель түзулерде немесе бір түзудің бойында жататын векторлар коллинеар векторлар деп аталады және 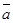 ||
|| 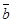 деп белгіленеді. Коллинеар векторлар бағыттас болуы да, қарама-қарсы бағытта да болуы мүмкін.
деп белгіленеді. Коллинеар векторлар бағыттас болуы да, қарама-қарсы бағытта да болуы мүмкін.
Егер екі 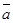 және
және 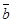 векторлары коллинеар болып, бағыттас және ұзындықтары бірдей болса, онда оларды тең векторлар (
векторлары коллинеар болып, бағыттас және ұзындықтары бірдей болса, онда оларды тең векторлар ( 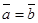 ) дейді. Тең векторлар еркін векторлар деп те аталады. Бұл векторлардың басталған нүктесін кеңістіктегі кез келген нүктеге көшіруге болады. Аналитикалық геометрияда еркін (бос) векторлар қарастырылады.
) дейді. Тең векторлар еркін векторлар деп те аталады. Бұл векторлардың басталған нүктесін кеңістіктегі кез келген нүктеге көшіруге болады. Аналитикалық геометрияда еркін (бос) векторлар қарастырылады.
Егер кеңістіктегі үш вектор бір жазықтықта немесе параллель жазықтықтарда жатса, онда олар компланар векторлар деп аталады.
