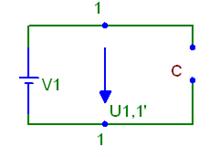
Алгебраическая сумма падений напряжений на элементах контура равна нулю

Вот и пригодились стрелки указывающие направление падения напряжения.

Применим метод создания алгебраической суммы, известный в математике как метод контурного интегрирования. Совершим обход контура по часовой стрелке через элементы V1, Ri, R, получим алгебраическую сумму, присваивая знак плюс рассматриваемой величине, если направление обхода совпадает с направлением падения напряжения и знак минус, если они противоположны.

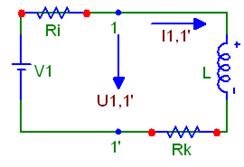
Помимо этого факта, можно установить способ определения величины R_i, опираясь на данные по проведению экспериментальных исследований на цепи, схема которой представлена на рис.4.

Очевидно, при достижении равенства R_i = R, в процессе изменения R, напряжение U_1,1' будет равно E/2.

В процессе вариации величины внешнего сопротивления можно добиться такого положения, что продолжая изменение, например, в сторону меньших значений, мы увидим , что показания амперметра перестают изменяться.

Очевидно, что этому состоянию соответствует соотношение между сопротивлениями

R_i>>R.

В этом случае данный источник относят к классу источников тока, поскольку ток в цепи не зависит от сопротивления элементов внешней части цепи.

Если будем изменять сопротивление R в сторону возрастания , то увидим, что напряжение U_1,1' начинает приближаться к Е, и наступает состояние, при котором напряжение на узлах 1,1 перестаёт меняться и при дальнейшем росте R перестаёт изменяться.

В этом случае, будет иметь место неравенство

R>>R_i.

В этом случае источник относят к классу источников напряжения.

Из приведенного анализа следует, что один и тот же источник энергии, в зависимости от соотношений между сопротивлениями может быть отнесён к одному или другому классу.

С-примитив

Рассмотрим другой элемент электротехники - конденсатор, подключив его вместо резистора.

Конденсатор является 2-х-полюсным элементом и физической сущностью его, в основном, является способность накапливать электрический заряд при условии замкнутости цепи, создавая тем самым, падение напряжения на элементе между его узлами.

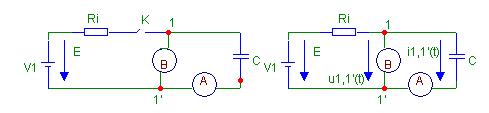
Рис.5а Рис.5б

На рис.5а показана схема до момента подключения источника (ключ К разомкнут). Источник энергии характеризуется ЭДС величиной Е=Const.

В момент времени, принимаемый за нуль (начало координат по независимой переменной t), замыкаем ключ К. Схема на рис.5б соответствует интервалу времени t≥0.

В момент подключения источника на амперметре будет наблюдаться резкое изменение величины тока в виде скачка (разрыв функции i1,1’(t)). Величина скачка в этот момент равна (рис.6).

.

Напряжение на узлах 1,1 в этот момент времени близко к нулю.

Этот экспериментальный результат показан на рис.6 в точках t, близких к нулю. В последующие моменты времени ток уменьшается до нуля (по амперметру), а напряжение становится равным ЭДС – Е (по вольтметру).

Рис.6.

Первое стационарное состояние – это выключенное состояние, второе стационарное состояние – это состояние, характеризуемое нулевым током и напряжением на узлах 1,1’ равным ЭДС.

Наблюдаемые явления в момент подключения, есть выражение процесса перехода из одного стационарного состояния в другое, т.е. переходный процесс.

С течением времениt наступает второе стационарное состояние, которое можно охарактеризовать как

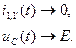. (1.2)

Этому положению соответствуют участки кривых при t больше нуля, вплоть до t2, которое условно может быть принято за точку ∞.

Оператор связи между током и напряжением можно записать, анализируя результат эксперимента по характеру изменения кривых на рис.6. В этом случае необходимо проведение большого числа экспериментов для оценки числовых коэффициентов. Проще полечить выражение связки следующим путём.

Второе стационарное состояние (при t → ∞) схемы можно описать формулой известной из физики электричества

Q_C = C*U_1,1' , (1.3)

в которой Q_C – величина заряда конденсатора, С – величина ёмкости, U_1,1' - напряжение на узлах 1,1'.

Если обратиться к интервалу времени, который начинается в момент включения, то формулу (1.2) можно записать в виде переменных от времени

q_C(t) = C*u(t)_1,1' , (1.4)

где

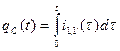, (1.5)

Тогда напряжение на конденсаторе можно записать формулой

. (1.6)

Возьмём производную по времени от обеих частей (1.5) и получим выражение для тока в момент t

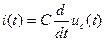. (1.7)

Соотношения (1.6), (1.7) можно положить в основу определения элемента теории электрических цепей, который назовём емкостным элементом.

Итак, емкостным элементом теории называется 2-х-полюсник, для которого соотношение между током и напряжением определяется только формулами (1.6) и (1.7).

Положение, при котором в рассматриваемой ветви схемы ток не протекает, как это следует из полученных в процессе эксперимента результатов (1.2), можно интерпретировать как нарушение токопрохождения путём разрыва этой ветви.

В этом случае емкостной элемент на схеме (именно на схеме, а не в цепи) может быть заменён 2-х-полюсным элементом, который назовём в теории как элемент типа «разрыв». Схема с подобным элементом приведена на рис.7.

Рис.7

Эта схема носит название эквивалентной,т.к. емкостной элемент заменён элементом типа «разрыв», который моделирует факт того, что ток равен нулю, но лишь при условии, что t → ∞.

Поскольку этот элемент и источник параллельны по отношению к узлам 1,1', напряжение одинаково для обоих и равно значению ЭДС источника.

1.1.3. L – примитив

Рассмотрим другой электротехнический элемент называемый катушкой индуктивности, которая представляет собой большое число витков медного провода, намотанного на сердечник из какого – либо магнитного материала, например, феррита, для увеличения магнитной индукции.

Следовательно, помимо индуктивности, данный элемент можно охарактеризовать и величиной резистивного сопротивления провода катушки. Желаемое действие катушки индуктивностей - является процесс формирования магнитного поля, если по проводнику, из которого изготовлены витки катушки будет наблюдаться ток. Резистивное действие проводника катушки – паразитный процесс, но свойственный данной конструкции.

Вследствие рассмотренного, катушку индуктивностей на схеме представим двумя последовательно включёнными элементами.

Почему применяем последовательное включение?

Это объясняется тем, что оба явления – резистивные потери в проводе катушки и формирование магнитного поля- определяются одним и тем же током.

Один из элементов - резистор R_k , представляет резистивные свойства проводника, другой – индуктивный элемент L, характеризующий способность формирования магнитного поля .

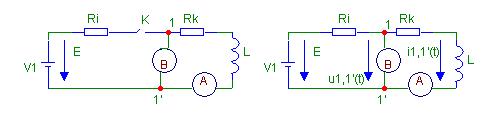
Рис.8а Рис.8б

На рис.8а показано состояние схемы, предшествующее подсоединению источника к цепи.

Замкнём ключ К, тем самым подсоединим катушку к источнику В этот момент времени вольтметр покажет величину напряжения, которая равна ВЕЛИЧИНЕ ЭДС, а амперметр покажет нуль тока.

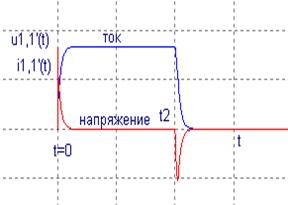
Рис.9.

С течением времени ток будет увеличиваться и достигнет некоторой постоянной величины, равной

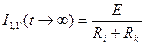, (1.8)

а напряжение на узлах 1,1' будет уменьшаться и приблизиться к величине, равной нулю. Это стационарное состояние может быть охарактеризовано величиной тока и напряжения на узлах 1.1'

I_1,1' =Е/( R_i + R_k) , U_1,1' =I_1,1' *R_k . (1.9)

Схема для определения величины тока при t → ∞ имеет вид, приведенный на рис.10.

Рис.10

На этой схеме напряжение на узлах 1,1 есть величина постоянная. Постоянной является также и величина тока, обозначенная на схеме как I_1,1'.

Оператор связи между током и напряжением можно записать, анализируя результат эксперимента по характеру изменения кривых на рис.9. В этом случае, необходимо проведение большого числа экспериментов для оценки числовых коэффициентов. Проще полечить выражение связки следующим путём.

Для второго стационарного состояния схемы ,учитывая постоянное значение тока и напряжения, можно записать формулу, которая определяет основное свойство катушки индуктивностей – величину потокосцепления Ψ

Ψ = LI_1,1'. (1.10)

Данной схеме (рис.10) на основе выражений (1.8) и (1.9) можно поставить в соответствие эквивалентную схему, в которой элемент индуктивный заменён элементом типа «короткое замыкание», поскольку напряжение формируется исключительно на омическом сопротивлении R_k.

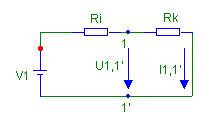
Рис.11

Вернёмся к моменту времени, соответствующему моменту подключения

t = 0.

Начиная с этого момента, и в течение некоторого интервала времени, ток и напряжение на узлах 1,1 есть величины переменные и для этих условий потокосцепление также переменная величина, следовательно, взяв производную по времени от обеих частей равенства (1.10) получим величину напряжения на рассматриваемых узлах в каждый текущий момент времени.

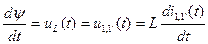. (1.11)

При t→0 производная может быть определена , следовательно, напряжение в этот момент времени существует, что и отражает кривая напряжения на рис.9.

Можно получить интегральный аналог данного выражения для определения тока в момент времени t.

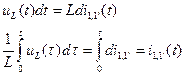. (1.12)

На основании полученных уравнений введём элемент теории цепей, который назовём индуктивным элементом.

Итак, индуктивным элементом ТЭЦ называется 2-х-полюсник, у которого напряжение и ток связаны только дифференциальным (1.11) или интегральным (1.12) оператором.

Рис.12

Во многих случаях резистивным элементом R_к будем пренебрегать, ввиду малости этой величины.

При t→∞ цепь переходит в стационарное состояние, которое прервём, разомкнув ключ К.

Опишем состояние рассмотренной цепи, начиная с момента размыкания ключа, т.е. с момента отключения источника постоянной ЭДС.

В момент размыкания ключа вольтметр покажет скачёк напряжения, показание же амперметра будет равно нулю.

Выводы :

1. В теории цепей достаточно для дальнейшего рассмотрения понимать, что напряжение (разность потенциалов между точками подсоединения вольтметра) можно рассматривать просто как показание вольтметра, а ток это некоторый процесс, величина которого представлена показаниями амперметра.

2. Каждый из 2-х-полюсников может быть описан в виде зависимости между током, который протекает через узлы, и напряжением на этих же узлах.

3. В общем случае электрической цепи можно приписать два различных состояния:

· стационарное, навязанный источником энергии и в рассмотренном случае это режим постоянного тока и постоянных во времени напряжений;

· переходное, или как его ещё называют – свободное, вызванный подключением источника к цепи. Процесс вызван скачкообразным изменением разности потенциалов на узлах 1,1.

4. На основе экспериментального материала получены первые математические формулы, которые, как мы увидим в дальнейшем, позволили построить теорию цепей в действительном (временном) и комплексном пространствах, что предопределило технические решения в построении электрических систем, например, связи.

5. Анализ экспериментальных кривых позволяет сформулировать определённые закономерности, которые носят названия законов коммутации. Эти законы отражают характер поведения – выражаемый через зависимости напряжения и тока 2-х-полюсника – в момент скачкообразного изменения напряжения или тока источника.